随机梯度下降算法的收敛性

• 随机梯度下降算法的调试
• 学习率 α 的选取

随机梯度下降算法的调试

在批量梯度下降中，我们可以令代价函数 J 为迭代次数的函数，绘制图表，根据图表来判断梯度下降是否收敛。但是，在大规模的训练集的情况下，这是不现实的，因为计算代价太大了。

在随机梯度下降中，我们在每一次更新$\theta$之前都计算一次代价，然后每 X 次迭代后，求出这 X 次对训练实例计算代价的平均值，然后绘制这些平均值与 X 次迭代的次数之间的函数图表。

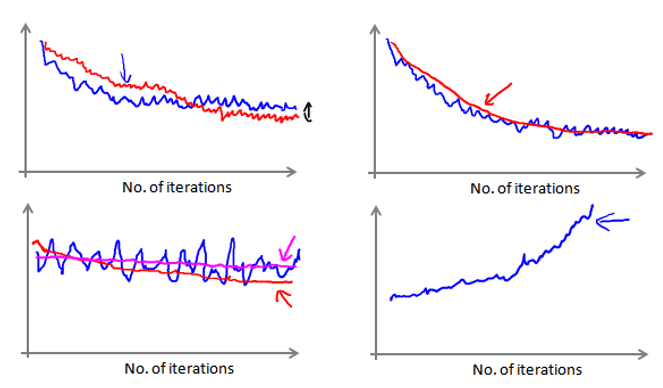
如果得到一个颠簸不平但是不会明显减少的函数图像（如上面左下图中蓝线所示）。我们可以增加 X 来使得函数更加平缓，也许便能看出下降的趋势（如上面左下图中红线所示）；或者可能函数图表仍然是颠簸不平且不下降的（如洋红色线所示），那么我们的模型本身可能存在一些错误。

如果我们得到的曲线如上面右下方所示，不断地上升，那么我们可能会需要选择一个较小的学习率 α。也可以令学习率随着迭代次数的增加而减小，例如令： $\alpha = \frac{const1}{iteratiobNumber + const2}$

随着我们不断地靠近全局最小值，通过减小学习率，我们迫使算法收敛而非在最小值附近徘徊。但是通常我们不需要这样做便能有非常好的效果了，对 α 进行调整所耗费的计算通常不值得。