理解反向传播
模型的学习优化体现在参数的改变上, 那么我们该怎么去改变它们呢?
这一节将帮助大家探索和理解优化算法的核心.
推理(前向传播)
学习反向传播之前, 我们先学习一下前向传播(9-3视频, 1 minutes 37 seconds, 可以查看吴恩达教授视频中的详细推导过程).
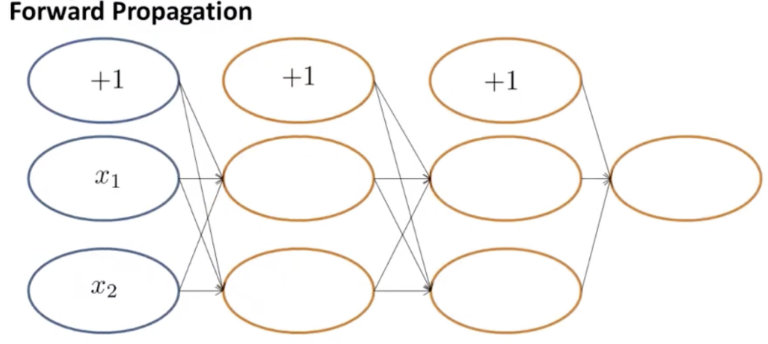
$x_1, x_2, +1$分别代表了输入和偏差项, 不考虑偏差项, 我们有两个输入, 两个隐藏层, 每个隐藏层有两个神经元, 最后有一个输出.
那么我们会有两个权重矩阵.$W_{hidden1}, W_{hidden2}$, 他们的$W_{shape} = (input_{num}, numofunits_{hidden})$
我们的计算公式为(这里是矩阵乘法)
我们来进行一个特例的计算
接下里我们来实战一下, 看看自己是否掌握了呢~
import numpy as np
def forward_progragation(inputs, weights):
if inputs.shape[1] != weights.shape[0]:
raise RuntimeError('维度不匹配, 请检查输入')
# todo 计算输出层
output = np.matmul(inputs, weights)
return output
inputs = np.random.uniform(size=(1, 3))
weights = np.random.uniform(size=(3, 1))
output = forward_progragation(inputs, weights)
print(output.shape)
assert output.shape == (1, 1), '输出结果不对, 请继续检查'
恭喜你, 现在你已经掌握了全连接网络的单层前向传播, 可以自己尝试多层的编写~
激活函数
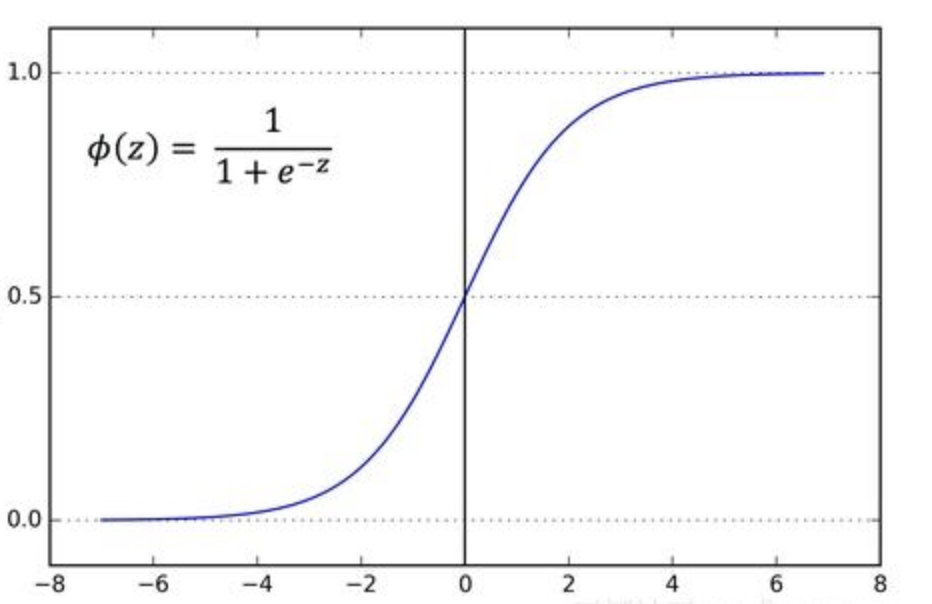
吴恩达教授有讲, 我们使用S型函数进行激活(视频, 3 minute 10 seconds), 我们来看一下S型函数的曲线以及表达式
我们来练习一下~
def sigmoid(x):
# todo 实现sigmoid激活函数
result = 1.0 / (1 + np.exp(-x))
return result
x = 0
result = sigmoid(x)
assert result == 0.5, '函数实现错了呢, 请修改'
现在我们已经掌握了层的计算以及激活函数的编写, 先表扬一下自己, 已经掌握了神经网络的基本骨架了, 多层网络只是对这种结构进行堆叠~
理解反向传播

接下来我们来一起看看反向传播.
反向传播
首先我们需要定义代价函数, 这是反向传播的第一步
代价函数的含义
代价函数代表的是我们模型的输出与真实值的差距, 越接近就代表我们的模型越准确, 那么我们的目标应该就是最小化这个损失, 模型输出和前面的权重有关(因为输入是固定的), 那么我们最后要的就是优化我们权重$W$, 方式就是对$W$求导了(我们的代价函数可以看做是关于$W$的函数), 可以得到变化最大的方向, 进行修正就完成了这个步骤了.
拓展
常用的代价函数
分类(交叉熵)
回归(MSE)
拓展小练习
我们来实现一下这几个函数(可选)
def cross_entropy(p, y):
log_p = np.log(p)
# todo 计算交叉熵
loss = (1.0 / n) * np.sum(np.multiply(y, p) + np.multiply(1 - y, p))
return loss
def mse(p, y):
if len(p) != len(y):
raise RuntimeError('样本数不一致')
loss = 1.0 / len(p)
loss *= np.sum(np.power((p - y), 2))
return loss
计算偏导数
理解反向传播
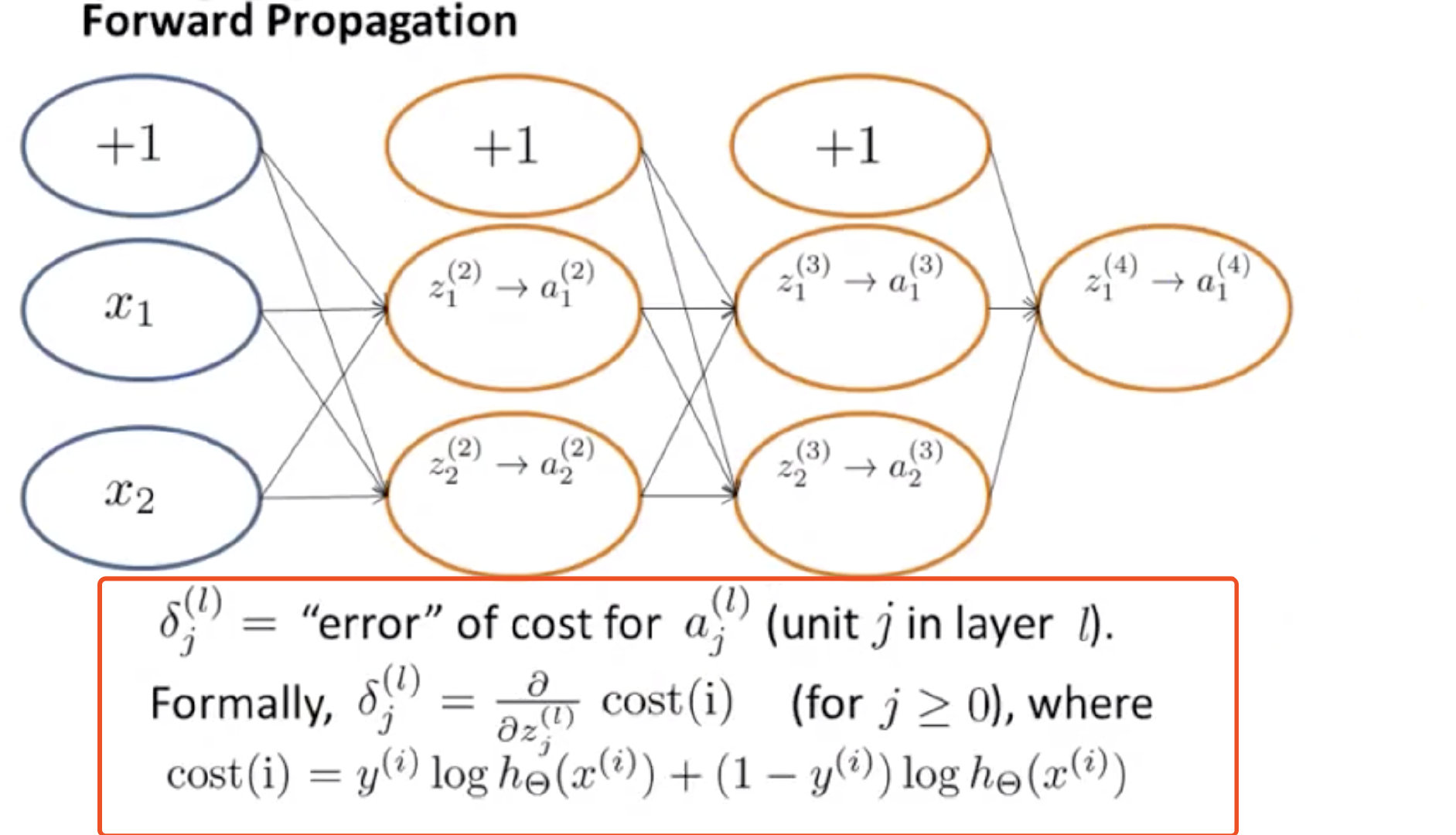
我们其实是在计算偏导数来进行更新的, 复合函数的求导其实就是链式法则
现在我们已经学习了前向, 反向传播, 我们接着来实现一个单隐藏层, 代价函数是 MSE 的神经网络
我们有$X => (1, 5)$, $W => (5, 1)$, $output => (1, 1)$, $loss = mse$的结构.
def mse(p, y):
if len(p) != len(y):
raise RuntimeError('样本数不一致')
loss = 1.0 / len(p)
loss *= np.sum(np.power((p - y), 2))
return loss
def forward_progragation(inputs, weights):
if inputs.shape[1] != weights.shape[0]:
raise RuntimeError('维度不匹配, 请检查输入')
output = np.matmul(inputs, weights)
return output
def back_progragation(error, x, p):
delta_error = (error - p)
dw = np.matmul(x.T, delta_error)
return dw
def net(x, w, y):
forward = forward_progragation(x, w)
loss = mse(forward, y)
dw = back_progragation(loss, x, forward)
print("forward:{0} \nloss:{1}\nbackward:\n{2}".format(forward, loss, dw))
x = np.random.uniform(size=(1, 5))
w = np.random.uniform(size=(5, 1))
y = np.array([[1]])
net(x, w, y)