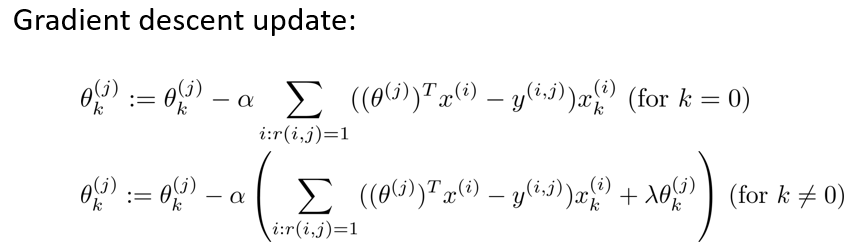基于内容的推荐系统

在一个基于内容的推荐系统算法中，假设对于我们希望推荐的东西有一些数据，这些数据是有关这些东西的特征。

在我们的例子中，我们可以假设每部电影都有两个特征，如$x_1$代表电影的浪漫程度，$x_2$代表电影的动作程度。

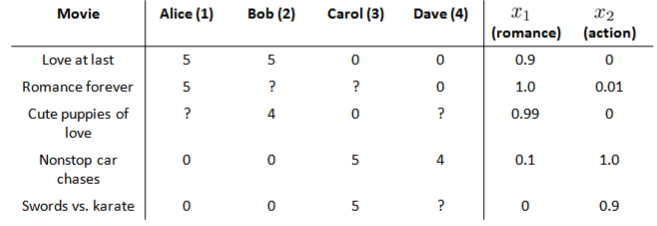
则每部电影都有一个特征向量，如 $x^{(1)}$是第一部电影的特征向量为[0.9 0]。

下面我们要基于这些特征来构建一个推荐系统算法。 假设我们采用线性回归模型，我们可以针对每一个用户都训练一个线性回归模型，如$\theta^{(1)}$ 是第一个用户的模型的参数。 则有：

• $\theta^{(j)}$: 用户 j 的参数向量
• $x^{(i)}$ 电影 i 的特征向量
• 对于用户 j 和电影 i，我们预测评分为：代价函数 $(\theta^{(j)})^Tx^{(i)}$
• 针对用户j，该线性回归模型的代价为预测误差的平方和，加上正则化项： $\min_{\theta_{(j)}}\frac{1}{2}\sum_{i:r(i,j) =1}((\theta^{(j)})^Tx^{(i)} - y^{(i,j)})^2 + \frac{\lambda}{2}(\theta^{(j)}_k)^2$

其中 $i:r(i,j)$表示我们只计算那些用户 j 评过分的电影。在一般的线性回归模型中，误差项和正则项应该都是乘以 1/2m，在这里我们将 m 去掉。并且我们不对方差项$\theta_0$进行正则化处理。

上面的代价函数只是针对一个用户的，为了学习所有用户，我们将所有用户的代价函数求和： $\min_{\theta_{(j)}}\frac{1}{2}\sum^{n_u}_{j=1}\sum_{i:r(i,j) =1}((\theta^{(j)})^Tx^{(i)} - y^{(i,j)})^2 + \frac{\lambda}{2}\sum^{n_u}_{j=1}\sum^{n}_{k=1}(\theta^{(j)}_k)^2$

如果我们要用梯度下降法来求解最优解，我们计算代价函数的偏导数后得到梯度下降的更新公式为：