压缩表示重建

给定的$z^{(i)}$，这可能 100 维，怎么回到你原来的表示$x^{(i)}$，这可能是 1000 维的数组？

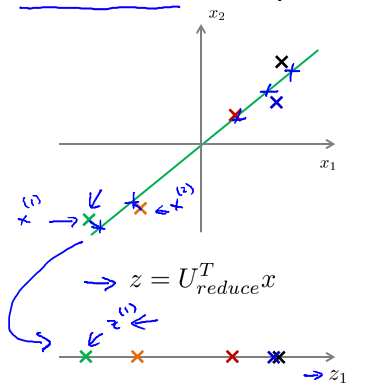
PCA 算法，有一个这样的样本。如图中样本 $x^{(1)}$,$x^{(2)}$。我们把这些样本投射到图中这个一维平面。然后现在我们需要只使用一个实数，比如 $Z^{(1)}$，指定这些点的位置后他们被投射到这一个三维曲面。给定一个点$z^{(1)}$，我们怎么能回去这个原始的二维空间呢？x 为 2 维，z 为 1 维， $z = U^T_{reduce}x$，相反的方程为：$x_{appox}=U_{reduce}z, x_{appox}\approx x$。如图：

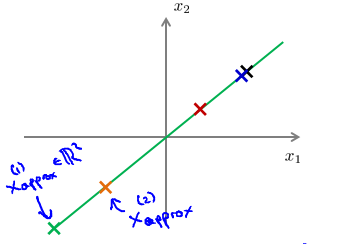
这是一个漂亮的与原始数据相当相似。所以，这就是你从低维表示 z 回到未压缩的表示。我们得到的数据的一个之间你的原始数据 x，我们也把这个过程称为重建原始数据。