优化目标

• K-均值的代价函数
• K-均值的迭代算法

K-均值的代价函数

K-均值最小化问题，是要最小化所有的数据点与其所关联的聚类中心点之间的距离之和，因此 K-均值的代价函数（又称畸变函数 Distortion function）为：

优化目标

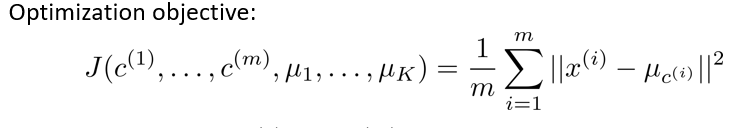
其中$\mu_{c^{(i)}}$代表与$x^{(i)}$ 最近的聚类中心点。优化目标便是找出使得代价函数最小的$c^{(1)},c^{(2)},…c^{(m)}$和 $\mu^1,\mu^2,…,\mu^k$。

回顾刚才给出的：

优化目标

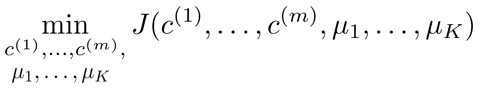
K-均值的迭代算法

K-均值迭代算法，第一个循环是用于减小$c^{(i)}$引起的代价，而第二个循环则是用于减小$\mu_i$引起的代价。迭代的过程一定会是每一次迭代都在减小代价函数，不然便是出现了错误。