反向传播
反向传播算法
计算神经网络预测结果的时候我们采用了一种正向传播方法,我们从第一层开始正向一层一层进行计算,直到最后一层的$h_\theta(x)$。
计算代价函数的偏导数$\frac{\partial}{\partial\theta^{(l)}_{ji}}j(\theta)$,我们需要采用一种反向传播算法,也就是首先计算最后一层的误差,然后再一层一层反向求出各层的误差,直到倒数第二层。
反向传播的实例
假设训练集只有一个实例$(x^{(1)},y^{(1)})$,神经网络是一个四层的神经网络,其中$K=4,S_L=4,L=4$:
前向传播算法:
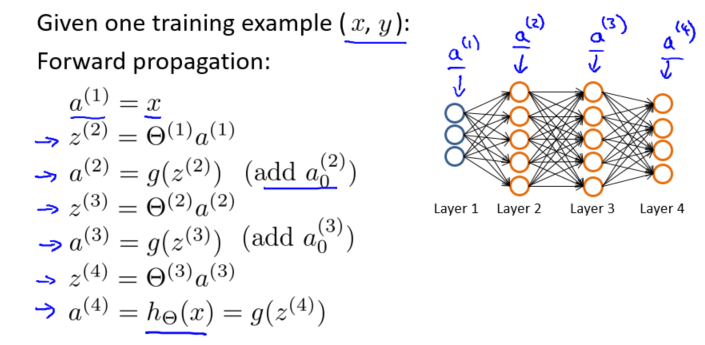
我们从最后一层的误差开始计算,误差是激活单元的预测$(a^{(4)}_k)$与实际值$(y^k)$之间的误差,$(k=1:K)$。
-
第四层:用δ来表示误差,则:$\delta^{(4)} = a^{(4)} -y$
-
第三层:利用$\delta^{(4)}$来计算前一层的误差:$\delta^{(3)} = (\theta^{(3)})^T(\delta)^{(4)} * g^`(z^{(3)})$
其中$g^`(z^{(3)})$是 S 形函数的导数,$g^`(z^{(3)})=a^{(3)}*(1-a^{(3)})$。而 $((\theta)^{(3)})^T(\delta)^{(4)}$ 则是权重导致的误差的和。 - 继续计算第二层的误差:$\delta^{(2)} = (\theta^{(2)})^T\delta^{(3)} * g^`(z^{(2)})$
- 第一层是输入变量,不存在误差。
有了所有的误差的表达式后,便可以计算代价函数的偏导数了,假设 $\lambda=0$,即我们不做任何正则化处理时有:
重要的是清楚地知道上面式子中上下标的含义:
- l 代表目前所计算的是第几层
- j 代表目前计算层中的激活单元的下标,也将是下一层的第 j 个输入变量的下标。
- i 代表下一层中误差单元的下标,是受到权重矩阵中第 i 行影响的下一层中的误差单元的下标。
如果我们考虑正则化处理,并且我们的训练集是一个特征矩阵而非向量。在上面的特殊情况中,我们需要计算每一层的误差单元来计算代价函数的偏导数。在更为一般的情况中,我们同样需要计算每一层的误差单元,但是我们需要为整个训练集计算误差单元,此时的误差单元也是一个矩阵,我们用$\Delta^{(l)}_{ij}$来表示这个误差矩阵。第 l 层的第 i 个激活单元受到第 j 个参数影响而导致的误差。
我们的算法表示为:

即首先用正向传播方法计算出每一层的激活单元,利用训练集的结果与神经网络预测的结果求出最后一层的误差,然后利用该误差运用反向传播法计算出直至第二层的所有误差。
在求出了$D^{(l)}_{ij}$之后,我们便可以计算代价函数的偏导数了,计算方法如下: