正则化与线性回归

• 如何通过正则化来解决线性回归过拟合问题

对于线性回归的求解，我们之前推导了两种学习算法：一种基于梯度下降，一种基于正规方程。

正则化线性回归的代价函数为：

$$J(\theta) = \frac{1}{2m} [ \sum_{i=1}^m(h_{\theta}(x^{(i)})-y^{(i)})^{2} + \lambda\sum_{j=1}^n\theta^2_j ]$$

如果我们要使用梯度下降法令这个代价函数最小化，因为我们未对$\theta_0$进行正则化，所以梯度下降算法将分两种情形：

对上面的算法中 $j=1,2,…,n$ 时的更新式子进行调整可得：
$\theta_j := \theta_j (1-a\frac{\lambda}{m})- \alpha \frac{1}{m}\sum^m_{i=1}(h_\theta(x^{(i)})-y^{(i)})x^{(i)}_j$

可以看出，正则化线性回归的梯度下降算法的变化在于，每次都在原有算法更新规则的基础上令$\theta$值减少了一个额外的值。

我们同样也可以利用正规方程来求解正则化线性回归模型，方法如下所示：

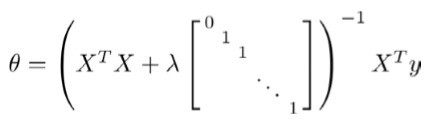
图中的矩阵尺寸为 (n+1)*(n+1)。

在前面讲过，如果 样本数 m 小于等于特征数 n 的时候，会遇到矩阵不可逆的问题，但是加入了正则项，可以证明到只要 $ \lambda > 0$ ,就可以解决不可逆的问题。