理解代价函数

代价函数的直观理解 I

本节强烈建议观看视频理解，以下仅列出关键步骤。

回顾上文，我们已经得到了单线性回归的模型：

hypothesis(假设):
$h_{0}(x) = \theta_{0} + \theta_{1}x$

parameters（参数）:
$\theta_{0}$ , $\theta_{1}$
通过选择不同的参数,会得到不同的直线拟合.

Cost Function(代价函数）:
$J(\theta_{0}, \theta_{1}) = \frac{1}{2m}\sum_{i=1}^m(h_{0}(x^{(i)})-y^{(i)})^{2}$

Goal:
$minimize_{\theta_{0},\theta_{1}}J(\theta_{0}, \theta_{1})$
我们的优化目标是,最小化代价函数

为理解方便，本节讲解中将h函数简化为$h_{0}(x) =\theta_{1}x$，即设$\theta_{0}=0$

首先明确一个概念：

• 在假设h中，$\theta_{1}$是一个固定的参数，只有$x$才是自变量。因变量为预测值 $h_{0}(x)$
• 在优化函数$J(\theta)$中，$\theta_{1}$是自变量，因变量为预测值$h_{0}(x)$与真实值$y$的误差$J(\theta)$

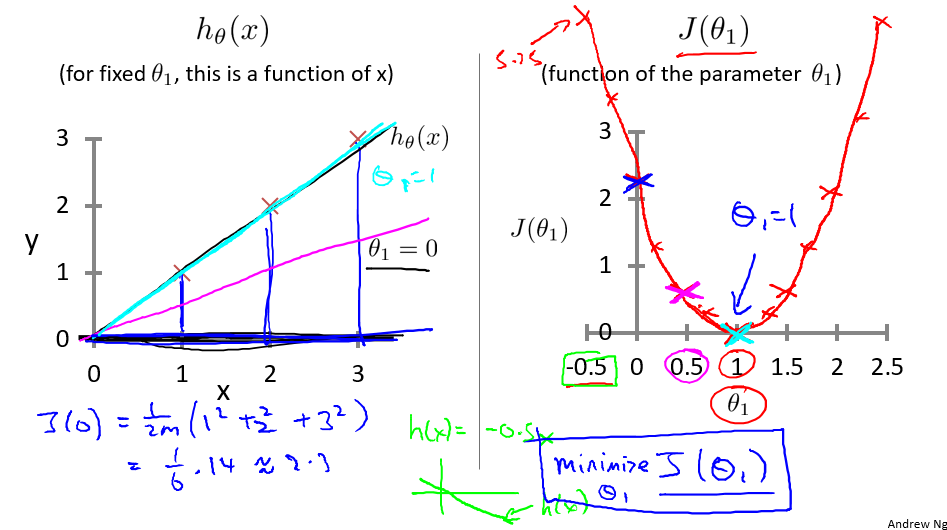
从这里开始,用实例来说明,不同的 $\theta_{1}$ , 代价函数的值.建议查看视频理解代价函数

由此我们可以画出假设h和优化函数$J(\theta)$对应的函数图像。