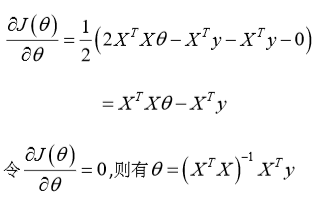正规方程不可逆的情况
- 正规方程 ( normal equation )的不可逆情况
- 正规方程解的推导过程
我们要讲的问题如下:
对于$\theta = (X^TX)^{-1}X^Ty$,当$X^TX$不可逆时该怎么办?
-
$X^TX$不可逆很少发生。 在Octave里,可逆矩阵求解逆使用inv(),不可逆矩阵求解伪逆使用pinv()。
-
使用大量的特征值的情况下,可能会导致矩阵$X^TX$的结果是不可逆的。
具体地说,在 m 小于或等于 n 的时候,例如,有 m 等于 10 个的训练样本也有 n 等于100 的特征数量。要找到适合的 ( n +1 ) 维参数矢量$\theta$ ,这将会变成一个 101 维的矢量,尝试从 10 个训练样本中找到满足 101 个参数的值,这工作可能会让你花上一阵子时间,但这并不总是一个好主意。因为,正如我们所看到你只有 10 个样本,以适应这 100 或 101 个参数,数据还是有些少。 稍后我们将看到,如何使用小数据样本以得到这 100 或 101 个参数,通常,我们会使用一种叫做正则化的线性代数方法,通过删除某些特征或者是使用某些技术,来解决当 m 比n 小的时候的问题。即使你有一个相对较小的训练集,也可使用很多的特征来找到很多合适的参数。
解决方法:

-
看特征值里是否有一些多余的特征,像这些 $x_1$和$x_2$是线性相关的,互为线性函数。删除重复的特征将解决不可逆性的问题。如果特征数量实在太多,可以删除些用较少的特征来反映尽可能多内容,或者考虑使用正则化方法。
-
如果矩阵$X^TX$是不可逆的,(通常来说,不会出现这种情况),如果在 Octave 里,可以用伪逆函数 pinv ( ) 来实现。即使 X’X 的结果是不可逆的,但算法执行的流程是正确的。
总之,出现不可逆矩阵的情况极少发生,所以在大多数实现线性回归中,不应该过多的关注$X^TX$不可逆。
正规方程解的推导过程
$\theta = (X^TX)^{-1}X^Ty$ 的推导过程: 其中: 将向量表达形式转为矩阵表达形式,则有$J(\theta) = \frac{1}{2}(X\theta - y)^{2}$,其中 X 为$mn$的矩阵(m为样本个数,n为特征个数),$\theta$为$n1$的矩阵,y 为$m*1$的矩阵,对$J(\theta)$进行如下变换:
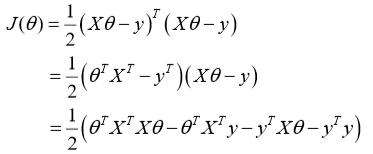
接下来对$J(\theta)$偏导,需要用到以下几个矩阵的求导法则: 对于(a)式:由于: $X^TAX = AX^2$ ,所以其导数为2AX 。 所以有: