直观理解大间距分类器
- 大间距分类器
- 直观理解SVM模型
- 对于参数C的选择
大间距分类器
这是支持向量机模型的代价函数
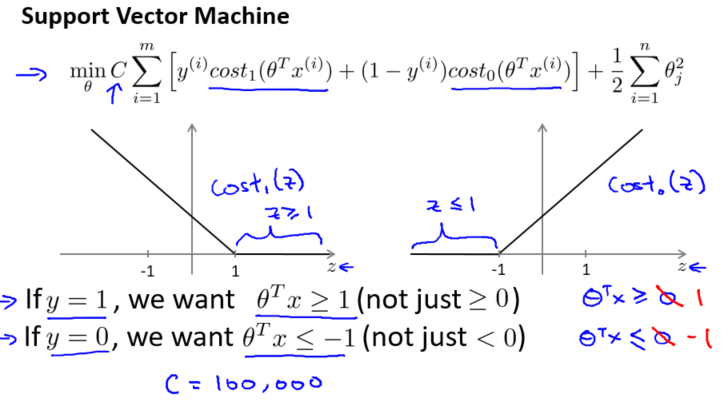
支持向量机的一个有趣性质——安全间距因子
如果你有一个正样本$y=1$,则只有在$z\geq1$时,代价函数$\cos t^{(z)}_1$才等于 0。换句话说,如果你有一个正样本,我们会希望 $\theta^Tx\ge1$,反之,如果$y=0$的,函数$\cos t^{(z)}_0$只有在$ z\leq1$的区间里函数值为0。事实上,如果你有一个正样本$y=1$,则仅仅要求 $\theta^Tx\ge0$,就能将该样本恰当分出,类似地,如果你有一个负样本,则仅需要 $\theta^Tx\leq0$就会将负例正确分离。
但是,支持向量机的要求更高,不仅仅要能正确分开输入的样本,即不仅仅要求 $\theta^Tx\ge0$,我们需要的是比 0 值大很多,比如大于等于 1,这就相当于在支持向量机中嵌入了一个额外的安全因子,或者说安全的间距因子。
安全间距因子的影响
考虑一个特例:我们将这个常数 C 设置成一个非常大的值,比如假设 C 的值为 100000,然后来观察支持向量机会给出什么结果。

如果 C 非常大,则最小化代价函数的时候,我们将会很希望找到一个使第一项为 0 的最优解。因此,让我们尝试在代价项的第一项为 0 的情形下理解该优化问题。
这将遵从以下的约束:如果$y^{(i)}=1$,则要求$\theta^Tx^{(i)}\geq1$;如果$y^{(i)}=0$,则要求$\theta^Tx^{(i)}\leq-1$;
这样当你求解这个优化问题的时候,当你最小化这个关于变量$\theta$的函数的时候,你会得到一个非常有趣的决策边界。
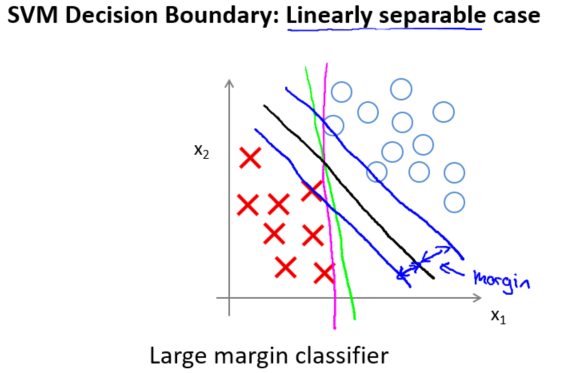
具体而言,如果你考察这样一个数据集,其中有正样本,也有负样本,可以看到这个数据集是线性可分的。我的意思是,存在一条直线把正负样本分开。当然有多条不同的直线,可以把正样本和负样本完全分开。支持向量机将会选择这个黑色的决策边界,相较于之前粉色或者绿色的决策边界。黑线看起来是更稳健的决策界。在分离正样本和负样本上它显得的更好。数学上来讲,这是什么意思呢?这条黑线有更大的距离,这个距离叫做间距 (margin)。 这个距离叫做支持向量机的间距,这是支持向量机具有鲁棒性的原因,因为它努力用一个最大间距来分离样本。因此支持向量机有时被称为大间距分类器。
异常点 (outlier)的影响
事实上,支持向量机现在要比这个大间距分类器所体现得更成熟,尤其是当你使用大间距分类器的时候,你的学习算法会受异常点 (outlier) 的影响。比如我们加入一个额外的正样本。
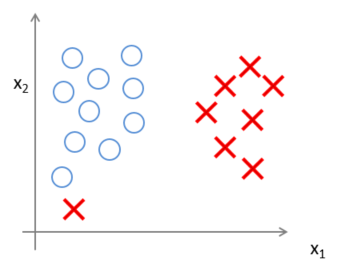
如果加了这个样本,为了将样本用最大间距分开,最终会得到一条类似粉色的线的决策界。仅仅基于一个异常值,仅仅基于一个样本,就将我的决策界从这条黑线变到这条粉线,这实在是不明智的。而如果正则化参数 C设置的非常大,支持向量机会将决策界从黑线变到了粉线,但是如果将 C 设置的不要太大,则你最终会得到这条黑线。
实际上,应用支持向量机的时候,当 C 不是非常非常大的时候,它可以忽略掉一些异常点的影响,得到更好的决策界。
回顾 C=1/λ,因此:
- C 较大时,相当于 λ 较小,可能会导致过拟合,高方差。
- C 较小时,相当于 λ 较大,可能会导致低拟合,高偏差。