选择主成分数目
主要成分分析是减少投射的平均均方误差:
训练集的方差为:$\frac{1}{m}(\sum)^{m}_{i=1}||(x)^{(i)}||^2$
我们希望在平均均方误差与训练集方差的比例尽可能小的情况下选择尽可能小的 k 值。
如果我们希望这个比例小于 1%,就意味着原本数据的偏差有 99%都保留下来了,如果我们选择保留 95%的偏差,便能非常显著地降低模型中特征的维度了。
可以先令 k=1,然后进行主要成分分析,获得$U_{reduce}$和 z,然后计算比例是否小于 1%。如果不是的话再令 k=2,如此类推,直到找到可以使得比例小于 1%的最小 k 值(原因是各个特征之间通常情况存在某种相关性)。
还有一些更好的方式来选择 k,当我们在 Octave 中调用“svd”函数的时候,我们获得三个参数:[U, S, V] = svd(sigma)。
其中的 S 是一个 n×n 的矩阵,只有对角线上有值,而其它单元都是 0,我们可以使用这个矩阵来计算平均均方误差与训练集方差的比例:
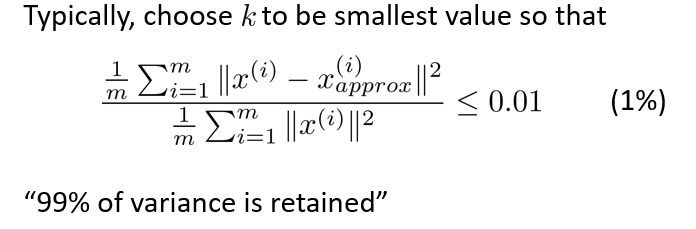
也就是:
在压缩过数据后,我们可以采用如下方法来近似地获得原有的特征: