优化问题
- 支持向量机(SVM)
- 由逻辑回归代价函数引入SVM代价函数
- SVM的假设
支持向量机(Support Vector Machine)是一个广泛应用于工业界和学术界的更加强大的算法。与逻辑回归和神经网络相比,支持向量机,或者简称 SVM,在学习复杂的非线性方程时提供了一种更为清晰,更加强大的方式。
这是逻辑回归的优化目标:
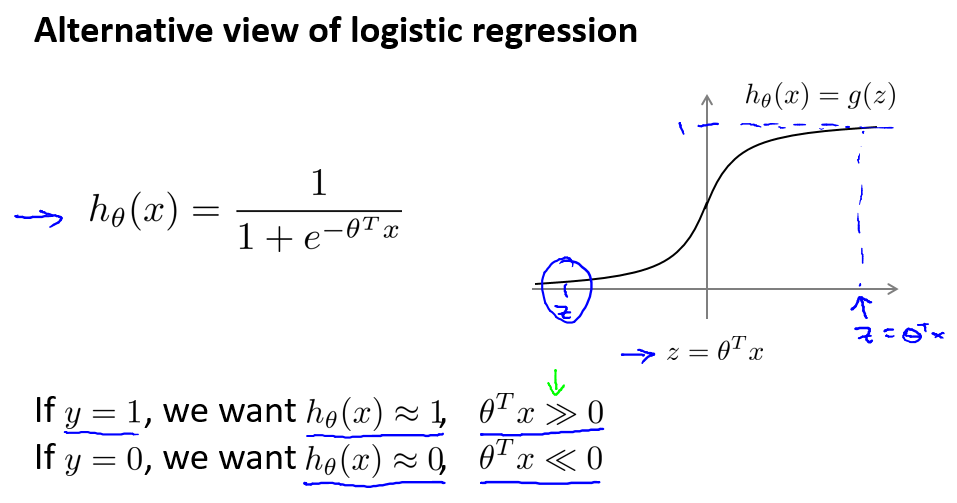
其中,用z来表示$\theta^Tx$。
在逻辑回归中:如果有一个$y=1$的样本,想要正确地将此样本分类,则$h_\theta(x)$要趋近1,这就意味着当$\theta^Tx$应当远大于$0$,这里的»意思是远远大于$0$。由于$z$表示$\theta^Tx$,当$z$远大于$0$时,即到了该图的右边,你不难发现此时逻辑回归的输出将趋近于$1$。相反地,如果有另一个样本$y=0$,那么我们希假设函数的输出值应该趋近于$0$,这对应于 $\theta^Tx$或者就是$z$会远小于 0。
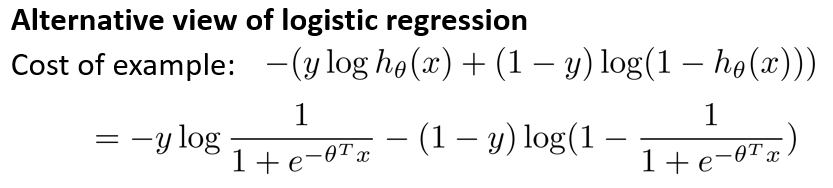
进一步观察逻辑回归的代价函数,会发现每个样本 (x, y)都会为总代价函数增加了一项,因此,对于总代价函数通常会有对所有的训练样本求和,并且还有一个 1/m 项,
现在,先忽略 1/m 这一项,但是这一项是影响整个总代价函数中的这一项的。一起来考虑两种情况:一种是 y 等于 1 的情况;另一种是 y 等于 0 的情况。
在第一种情况中,假设 y=1,此时在目标函数中只需有第一项起作用,因为 y 等于 1 时,(1-y) 项将等于0。因此,当在 y=1 的样本中时,即在 (x, y) 中 y 等于 1,我们得到这样一项$-log(1-\frac{1}{1 + e^{-z}})$:
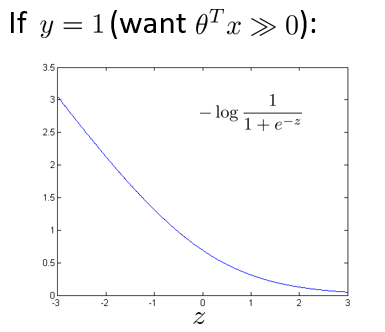
用z来表示$\theta^Tx$。当然,在代价函数中,y 前面有负号。如果画出关于 z 的函数,你会看到这条曲线,当 z 增大时,也就是$\theta^Tx$增大时,z 对应的值会变的非常小。对整个代价函数而言,影响也非常小。这也就解释了,为什么逻辑回归在观察到正样本 y=1 时,试图将$\theta^Tx$设置得非常大。因为,在代价函数中的这 一项会变的非常小。
代价函数的设计</span>
逻辑回归的代价函数,也就是$-log(1-\frac{1}{1 + e^{-z}})$。取z=1 点,先画出将要用的代价函数。 然后我再画一条同逻辑回归非常相似的直线,但是,在这里是一条直线,也就是我用紫红色画的曲线,就是这条紫红色的曲线。
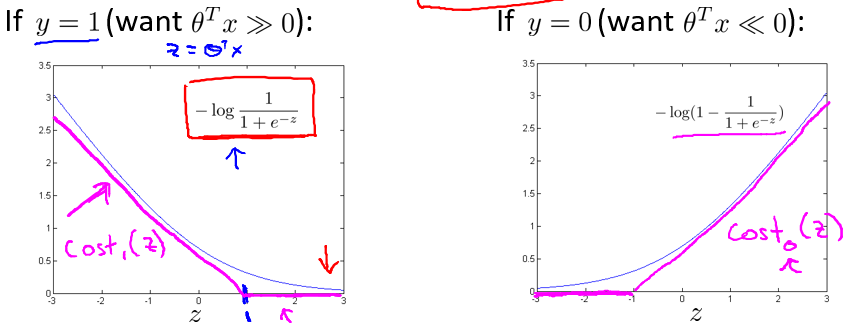
给这两个方程(紫红色曲线)命名,左边的函数为$\cos t^{(z)}_1$,右边函数为$\cos t^{(z)}_0$ 。下标是指在代价函数中对应的 y=1 和 y=0 的情况.
这是我们在逻辑回归中使用代价函数$J(\theta)$,将负号移到了表达式的里面:
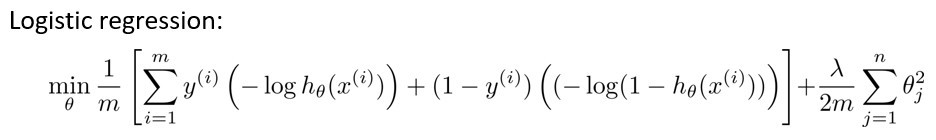
对于支持向量机而言,实质上我们要将这替换为$\cos t^{(z)}_1$ ,也就是 $\cos t^{(\theta^Tx)}_1$ ,同样地,我也将这一项替换为$\cos t^{(\theta^Tx)}_0$。这里的代价函数$\cos t^{(\theta^Tx)}_1$,就是之前所提到的那条线。然后,再加上正则化参数。对于支持向量机,我们得到了这里的最小化问题,即:
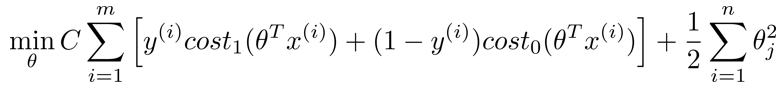
这个公式有一些不同:
- 1/m 这一项被除去。仅仅是由于人们使用支持向量机时的习惯所致,1/m 仅是个常量不影响最终得到的最优值$\theta$。
- 概念上的变化。训练样本的代价表示为A,正则化项为B。逻辑回归的目标函数为$A+\lambda B$,通过设置不同正则参数$\lambda$达到优化目的,即最小化A。但对于支持向量机,目标函数为$C×A+B$,这里的参数 C 可以考虑成$\frac{1}{\lambda}$,同 1/λ 所扮演的角色相同。,这只是一种不同的方式来控制这种权衡或者一种不同的方法,即用参数来决定是更关心代价函数的优化,还是更关心正则项的优化。
支持向量机的假设

最后有别于逻辑回归输出的概率。在这里,我们的代价函数,获得参数$\theta$时,支持向量机所做的是它来直接预测 y 的值等于 1,还是等于 0。