大间距分类器背后的数学原理 (选学)

• 大间距分类器的数学实现
• 向量的内积
• SVM的目标函数

向量内积

假设有两个向量，u和v，都是二维向量。$u^Tv$叫做向量u 和v之间的内积。

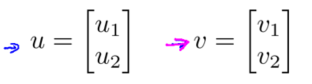
将两个向量画在图上。

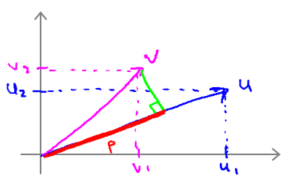
向量u在横轴上，取值为某个$u_1$，而在纵轴上，高度是$u_2$作为u的第二个分量。现在，很容易计算的一个量就是向量u的范数$\|u\|$,即向量$u$的欧几里得长度。根据毕达哥拉斯定理， $\|u\|=\sqrt{u_1^2+u_2^2}$，这是向量u的长度，它是一个实数。

计算u和v之间的内积的几何做法，我们将向量v做一个直角投影到向量u上，度量这条红线的长度p，因此 p 就是向量v投影到向量u上的量。因此可以将$u^Tv=p\cdot\|u\|$ 。

另一种线性代数方法，$u^Tv=u_1\times v_1+u_2\times v_2$,会给出同样的结果。

顺便，有$u^Tv=v^Tu$。

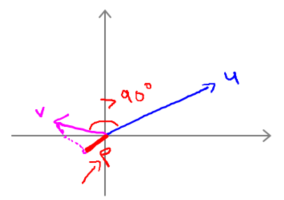
需要注意的就是p值是有符号的，即它可能是正值，也可能是负值。如下图，如果u 和v之间的夹角大于 90 度，则如果将v投影到u 上，会得到这样的一个投影，这是 p 的长度，在这个情形下我们仍然有

$u^Tv=p\cdot\|u\|$，唯一一点不同的是 p 在这里是负的。在内积计算中，如果u 和v之间的夹角小于 90 度，那么那条红线的长度 p 是正值。然而如果这个夹角大于 90 度，则 p 将会是负的。就是这个小线段的长度是负的。如果它们之间的夹角大于 90 度，两个向量之间的内积也是负的。

SVM的目标函数

这就是我们先前给出的支持向量机模型中的目标函数。接下来忽略掉截距，令$\theta_0=0$，这样更容易画示意图。假设特征数 n = 2，则仅有两个特征$x_1$,$x_2$。 此时，支持向量机的优化目标函数可以写作： $\min_\theta\frac{1}{2}\sum^n_{j=1}\theta^2_j = \frac{1}{2}(\theta^2_1+\theta^2_2) = \frac{1}{2}\sqrt{\theta_1^2+\theta_2^2}=\frac{1}{2}||\theta||^2$

当然你可以将其写作$\theta_0,\theta_1,\theta_2$，但是，数学上不管你是否包含，其实并没有差别，因此在我们接下来的推导中去掉$\theta_0$不会有影响这意味着我们的目标函数是等于 $\frac{1}{2}||theta||^2$。因此支持向量机做的全部事情，就是极小化参数向量$\theta$范数的平方。

现在我们将要深入地理解$\theta^Tx$。给定参数向量$\theta$给定一个样本$x^{(i)}就类似于u和v。

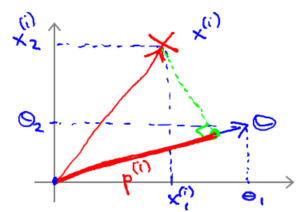
使用我们之前的方法，我们计算的方式就是我将训练样本投影到参数向量$\theta$，然后我来看一看这个线段的长度，我将它画成红色。我将它称为$ p^{(i)}$用来表示这是第i个训练样本在参数向量$\theta$上的投影,$\theta^Tx$将会等于p乘以向量$\theta$的长度或范数。

这里表达的意思是：这个$\theta^Tx^{(i)} \geq1$或者$\theta^Tx^{(i)} < -1$的,约束是可以被$p^{(i)} \cdot x \geq 1$这个约束所代替的。我们的优化目标就变成了$p^{(i)} \cdot x$。

需要提醒一点，我们之前曾讲过这个优化目标函数可以被写成等于$\frac{1}{2}\|\theta\|^2$ 。

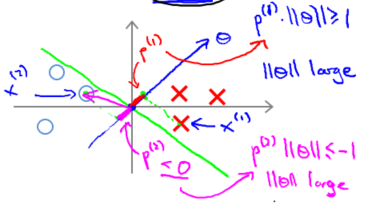
假设支持向量机会选择这个绿色决策边界。这不是一个非常好的选择，因为它的间距很小。这个决策界离训练样本的距离很近。我们来看一下为什么支持向量机不会选择它。

对于这样选择的参数$\theta$，可以看到参数向量$\theta$。事实上是和决策界是 90 度正交的，因此这个绿色的决策界对应着一个参数向量$\theta$指向这个方向,顺便提一句$\theta_0=0$的简化仅仅意味着决策界必须通过原点 (0,0)。现在让我们看一下这对于优化目标函数意味着什么。

比如这个样本，我们假设它是我的第一个样本$x^{(1)}$，如果我考察这个样本到参数$\theta$的投影，投影是这个短的红线段，就等于$p^{(1)}$。类似地，样本$x^{(2)}$，它到$\theta$的投影在这里。投影是这个短的粉线段$p^{(2)}$，它事实上是一个负值。

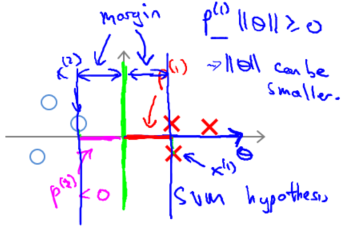
如果这是决策界，这就是相对应的参数 θ 的方向，因此，在这个决策界之下，垂直线是决策界。使用线性代数的知识，可以说明，这个绿色的决策界有一个垂直于它的向量$\theta$ 。现在如果你考察你的数据在横轴 x 上的投影，比如这个我之前提到的样本，我的样本 $x^{(1)}$，当我将它投影到横轴 x 上，或说投影到 θ 上，就会得到这样的$p^{(1)}$。它的长度是 $p^{(1)}$，另一个样本，那个样本是 x(2)。我做同样的投影，我会发现，$p^{(2)}$的长度是负值。你会注意到现在$p^{(1)}$和$p^{(2)}$这些投影长度是长多了。如果我们仍然要满足这些约束，$p^{(i)} \cdot x > 1$，这意味着通过选择右边的决策界，而不是左边的那个，支持向量机可以使参数$\theta$的范数变小很多。因此，如果我们想令$\theta$的范数变小，从而令$\theta$范数的平方变小，就能让支持向量机选择右边的决策界。这就是支持向量机如何能有效地产生大间距分类的原因。

看这条绿线，这个绿色的决策界。我们希望正样本和负样本投影到 θ 的值大。要做到这一点的唯一方式就是选择这条绿线做决策界。这是大间距决策界来区分开正样本和负样本这个间距的值。这个间距的值就是$p^{(1)}$,$p^{(2)}$,$p^{(3)}$等等的值。通过让间距变大，即通过这些$p^{(1)}$,$p^{(2)}$,$p^{(3)}$等等的值，支持向量机最终可以找到一个较小的$\theta$范数。这正是支持向量机中最小化目标函数的目的。

以上就是为什么支持向量机最终会找到大间距分类器的原因。因为它试图极大化这些$p^{(i)}$的范数，它们是训练样本到决策边界的距离。

最后一点，我们的推导自始至终使用了这个简化假设，就是参数 $\theta_0=0$。它能够让决策界通过原点。如果你令 $\theta_0$不是 0 的话，含义就是你希望决策界不通过原点。我将不会做全部的推导。实际上，支持向量机产生大间距分类器的结论，会被证明同样成立，证明方式是非常类似的，是我们刚刚做的证明的推广。