模型表示 II

大脑中的神经网络是怎样的？

前向传播算法( FORWARD PROPAGATION ) 相对于与使用循环来编码，利用向量化的方法会使得计算更为简便。

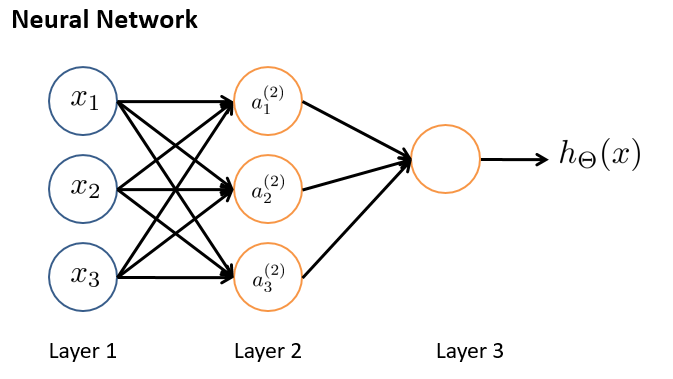
以上面的神经网络为例，试着计算第二层的值：

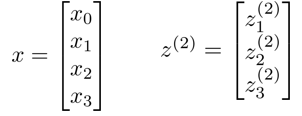
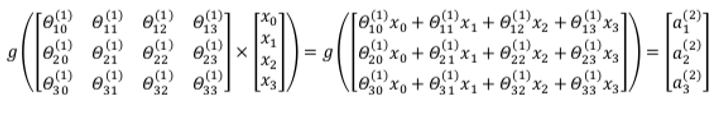
我们令 $z^{(2)}=\theta^{(1)}x$ ，则 $a^{(2)}=g(z^{(2)})$ ，计算后添加 $a^{(2)}_0=1$ 。计算输出的值为：

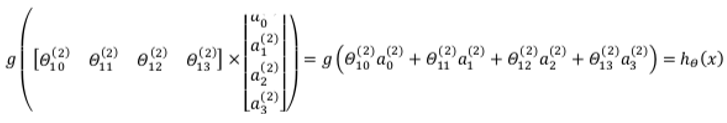
我们令 $z^{(3)}=\theta^{(2)}a^{(2)}$ ，则 $h_\theta(x)=a^{(3)}=g(z^{(3)})$ 。

这只是针对训练集中一个训练实例所进行的计算。如果我们要对整个训练集进行计算，我们需要将训练集特征矩阵进行转置，使得同一个实例的特征都在同一列里。即： $z^{(2)}=\theta^{(1)}\times{X^T}$ $a^{(2)} = g(z^{(2)})$

为了更好了了解 Neuron Networks 的工作原理，我们先把左半部分遮住：

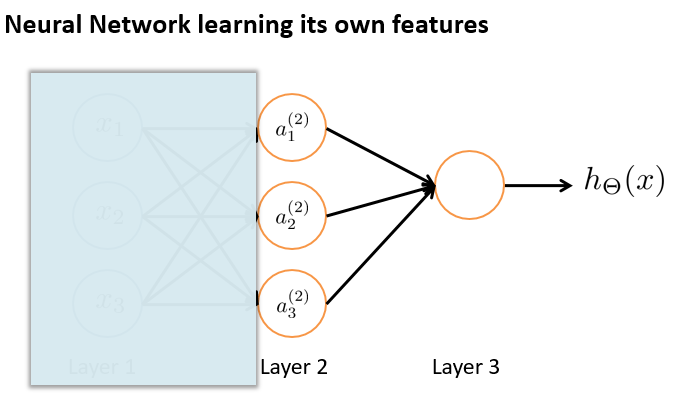
右半部分其实就是以 $a_0, a_1, a_2, a_3$ ,按照 Logistic Regression 的方式输出 $h_\theta(x)$ ：

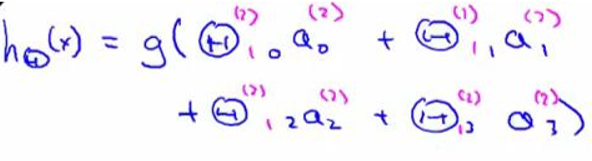
我们可以把 $a_0, a_1, a_2, a_3$ 看成更为高级的特征值，也就是 $x_0, x_1, x_2, x_3$ 的进化体，并且它们是由 x 与 $\theta$ 决定的，因为是梯度下降的，所以 a 是变化的，并且变得越来越厉害，所以这些更高级的特征值远比仅仅将 x 次方厉害，也能更好的预测新数据。这就是神经网络相比于逻辑回归和线性回归的优势。

牛刀小试

我们假设没有激活函数

# todo 实现上图绘制的神经网络, 我们可以采用 np.random.uniform(size=())去随机生成参数
import numpy as np

def sigmoid(x):
    return 1/(1+np.exp(-x))

def net():
    # todo 确定输入和权重的维度
    X = np.array([[1],[-2],[3],[-4]])
    theta1 = np.random.uniform(size=(3, 4))
    hidden_input = sigmoid(np.matmul(theta1,X))
    print('hidden_input',hidden_input)
    hidden_input = np.insert(hidden_input, 0, [1], axis=0)
    print('hidden_input',hidden_input)
    theta2 = np.random.uniform(size=(1, 4))
    output = sigmoid(np.matmul( theta2,hidden_input))
    return output


    
  