矩阵转置与求逆

矩阵的逆

矩阵 A 是一个 m×m 矩阵（方阵），如果有逆矩阵，则： $AA^{-1} = A^{-1}A = I$

没有逆矩阵的矩阵, 称为奇异 (singlar/degenerate)矩阵

import numpy as np

a = np.mat([[1,2],[3,4]])
print ('a:\n',a)

a:
 [[1 2]
 [3 4]]

# 计算 矩阵 a 逆矩阵
res = np.linalg.inv(a)
print('a inverse:\n', res)

a inverse:
 [[-2.   1. ]
 [ 1.5 -0.5]]

矩阵的转置

设 A 为 m×n 阶矩阵（即 m 行 n 列），第 i 行 j 列的元素是 a(i,j)，即：A=a(i,j) 定义 A 的转置为这样一个 n×m 阶矩阵 B，满足 B=a(j,i)，即 b (i,j)=a (j,i)（B 的第 i 行第 j 列元素是 A 的第 j 行第 i 列元素），记 $A^T=B$。

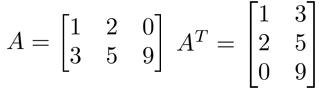
直观来看，将 A 的所有元素绕着一条从第 1 行第 1 列元素出发的右下方 45 度的射线作镜面反转，即得到 A 的转置。

a = np.mat([[1,2],[3,4]])
print ('a:\n',a)

a:
 [[1 2]
 [3 4]]

# todo: 计算 矩阵 a 转置
res = a.T
print('a transpose:\n', res)

a transpose:
 [[1 3]
 [2 4]]

矩阵的转置基本性质

$(A \pm B)^T = A^T \pm B^T $
$(A \times B)^T = A^T \times B^T $
$(A^T)^T = A $
$(KA)^T = KA^T $