正规方程

• 正规方程
• 梯度下降与正规方程的比较

对于某些线性回归问题，正规方程方法是更好的解决方案。如：

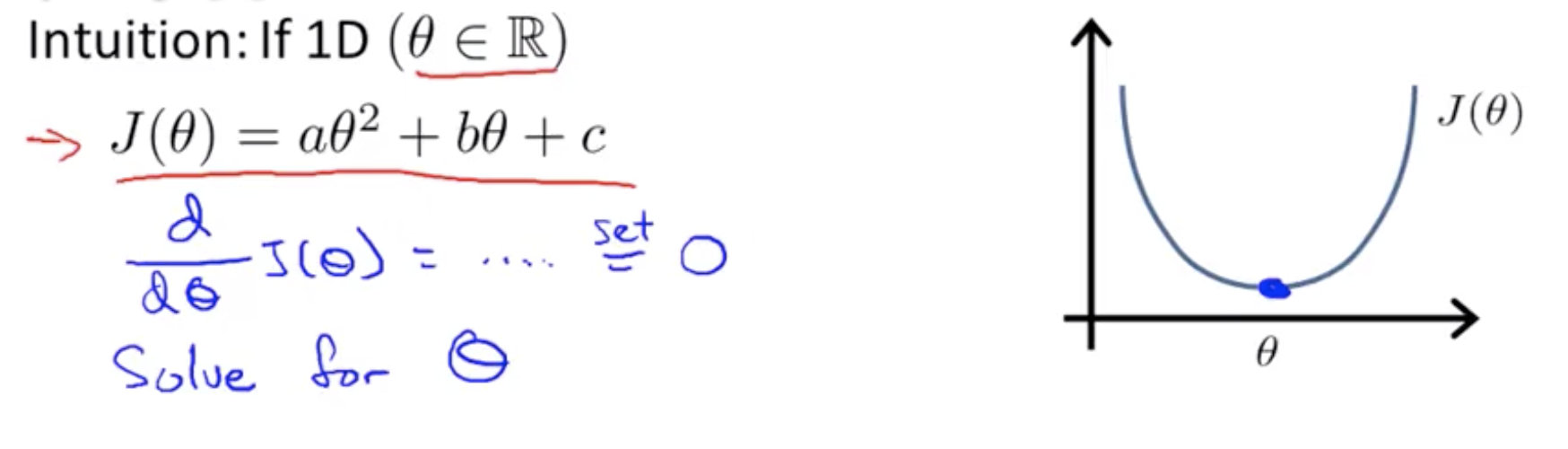
正规方程是通过求解下面的方程, 求解代价函数的梯度等于 0, 来找出使得代价函数最小的参数的： $\frac{\partial}{\partial{\theta_{j}}}J(\theta_j) = 0$

假设我们的训练集特征矩阵为 X（包含了$x_0=1$）并且我们的训练集结果为向量 y， 则利用正规方程解出向量$\theta = (X^TX)^{-1}X^Ty$
上标 T 代表矩阵转置，上标-1 代表矩阵的逆。设矩阵$A =X^TX$，则：$(X^TX)^{-1} = A^{-1}$

以下表的数据为例, 直接运用正规方程方法求解参数：

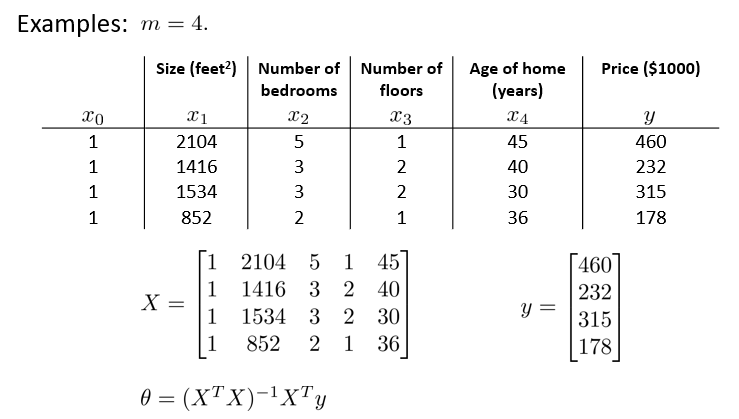
注：对于那些不可逆的矩阵（通常是因为特征之间不独立，如同时包含英尺为单位的尺寸和米为单位的尺寸两个特征，也有可能是特征数量大于训练集的数量），正规方程方法是不能用的。（其实也可以使用，详细讨论在04-7）

梯度下降与正规方程的比较

总结一下，只要特征变量的数目并不大，标准方程是一个很好的计算参数$\theta$的替代方法。具体地说，只要特征变量的数量小于一万，通常使用标准方程法，而不使用梯度下降法。

随着我们要讲的学习算法越来越复杂，例如，分类算法的逻辑回归算法，我们会看到， 实际上对于那些算法，并不能使用正规方程法。对于那些更复杂的学习算法，我们将不得不仍然使用梯度下降法。因此，梯度下降法是一个非常有用的算法，可以用在有大量特征变量的线性回归问题。或者我们以后在课程中，会讲到的一些其他的算法，因为正规方程法不适合或者不能用在它们上。但对于这个特定的线性回归模型，标准方程法是一个比梯度下降法更快的替代算法。所以，根据具体的问题，以及你的特征变量的数量，这两种算法都是值得学习的。

牛刀小试

# 正规方程的 python 实现
import numpy as np
def normalEqn(X, y):
    theta = np.linalg.inv(X.T@X)@X.T@y        #X.T@X 等价于 X.T.dot(X)
    return theta