代价函数 III

• 神经网络的代价函数

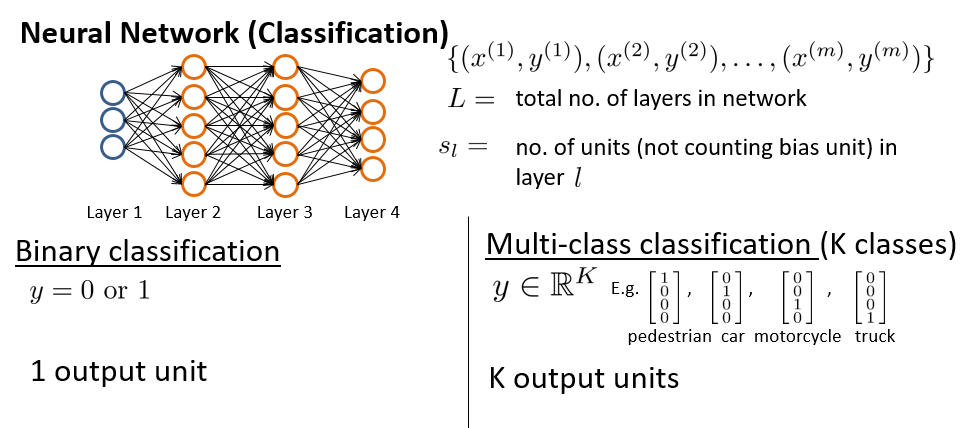
标记约定

假设神经网络的训练样本有 m 个，每个包含一组输入 x 和一组输出信号 y，L 表示神经网络层数，$S_I$表示每层的 neuron 个数( SL表示输出层神经元个数)，$S_L$代表最后一层中处理单元的个数。

神经网络分类问题

将神经网络的分类定义为两种情况：二类分类和多类分类，

• 二类分类： $S_L=1$, y=0 or 1表示哪一类；
• K 类分类： $S_L=K$,$y_i$表示分到第 i 类；（K > 2）

代价函数

在逻辑回归中，我们只有一个输出变量，又称标量（scalar），也只有一个因变量 y,逻辑回归问题中代价函数为：

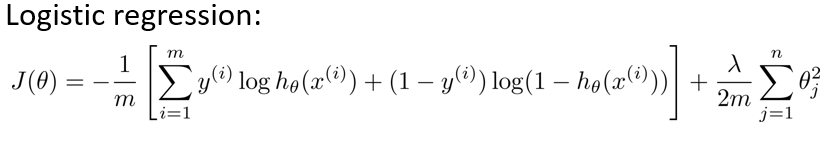
但是在神经网络中，可以有很多输出变量，我们的$h_\theta(x)$是一个维度为 K 的向量，并且训练集中的因变量也是同样维度的一个向量，因此我们的代价函数会比逻辑回归更加复杂一些。

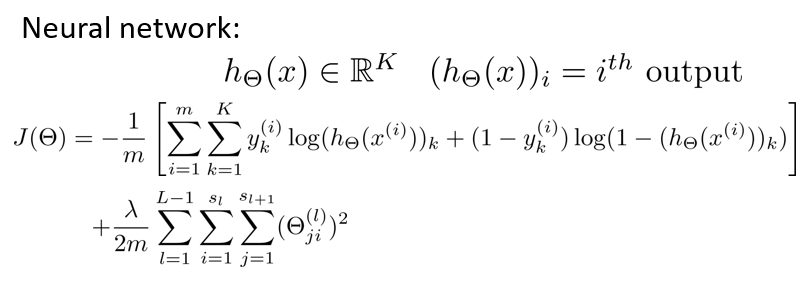
通过代价函数来观察算法预测的结果与真实情况的误差有多大，与逻辑回归唯一不同的是，对于每一行特征，我们都会给出 K 个预测，基本上我们可以利用循环，对每一行特征都预测 K 个不同结果，然后在利用循环 在 K 个预测中选择可能性最高的一个，将其与 y 中的实际数据进行比较。

正则化的那一项只是排除了每一层$\theta^{(0)}$后，每一层的矩阵$\theta$的和。最里层的循环 j 循环所有的行（由 $s_l + 1$层的激活单元数决定），循环 i 则循环所有的列，由该层（$s_l$层）的激 活单元数所决定。即：$h_\theta(x)$与真实值之间的距离为每个样本-每个类输出的加和，对参数进行 regularization 的 bias 项处理所有参数的平方和。