理解代价函数 II

代价函数的直观理解 II -等高线

本节强烈建议观看视频理解，以下仅列出关键步骤。

本节中，我们将结合等高线图，更深入地学习代价函数的作用。

照例先给出单线性回归模型： hypothesis(假设):
$h_{0}(x) = \theta_{0} + \theta_{1}x$

parameters（参数）:
$\theta_{0}$ , $\theta_{1}$

Cost Function(代价函数）:
$J(\theta_{0}, \theta_{1}) = \frac{1}{2m}\sum_{i=1}^m(h_{0}(x^{(i)})-y^{(i)})^{2}$

Goal:
$minimize_{\theta_{0},\theta_{1}}J(\theta_{0}, \theta_{1})$

在上一节中，我们假设$\theta_0=0$，仅考虑了$\theta_1$, 得到的图像是一个弓形曲线：

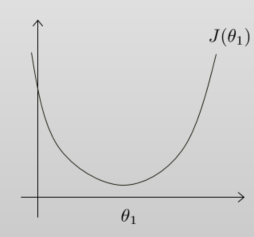
如果我们考虑$[\theta_0, \theta_1]$两个参数，得到的图像则如下：

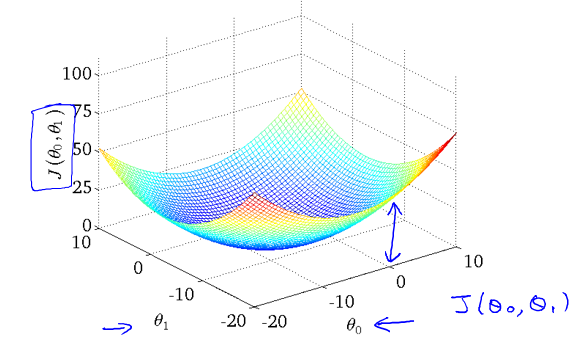
从代价函数的样子（等高线图）中可以看出在三维空间中存在一个使得 $J(\theta_{0}, \theta_{1})$最小的点。

下面为等高线图的二维图像，同一线圈上的 $J(\theta_{0}, \theta_{1})$取值相同。

理解代价函数

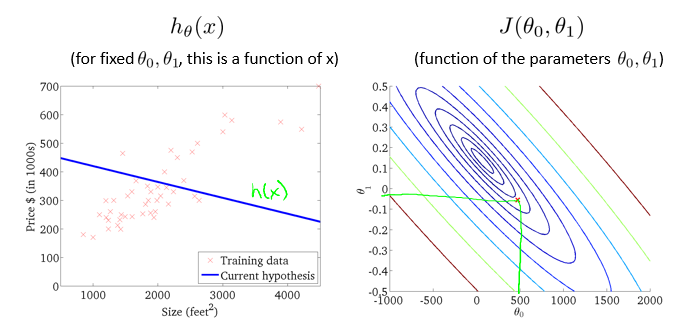
通过这些图形，我希望你能更好地理解这些代价函数$J$所表达的值是什么样的，它们对应的假设是什么样的，以及什么样的假设对应的点，更接近于代价函数 $J$ 的最小值。

当然，我们真正需要的是一种有效的算法，能够自动地找出这些使代价函数$J$取最小值的参数 $\theta_{0}$ 和 $\theta_{1}$来。

我们也不希望编个程序把这些点画出来，然后人工的方法来读出这些点的数值，这很明显不是一个好办法。我们会遇到更复杂、更高维度、更多参数的情况，而这些情况是很难画出图的，因此更无法将其可视化，因此我们真正需要的是编写程序来找出这些最小化代价函数的 $\theta_{0}$和$\theta_{1}$的值。

在下一节视频中，我们将介绍一种算法，能够自动地找出能使代价函数$J$最小化的参数$\theta_{0}$和$\theta_{1}$的值。