代价函数

定义代价函数用来拟合逻辑回归的参数，这便是监督学习问题中的逻辑回归模型的拟合问题。

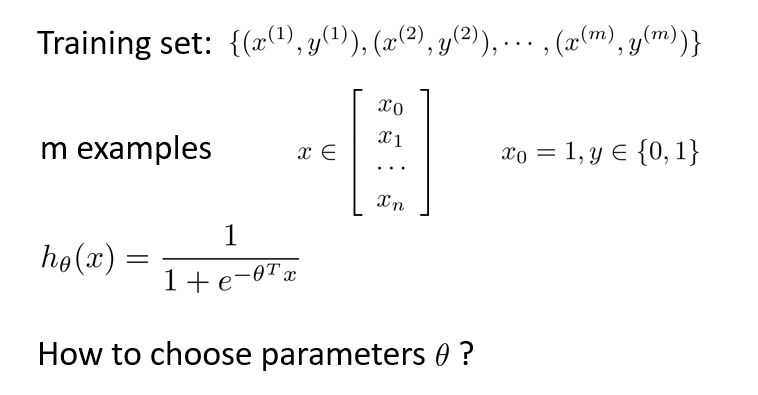
线性回归模型的代价函数是所有模型误差的平方和。理论上来说，对逻辑回归模型也可以沿用这个定义，但是问题在于，当我们将 $h_\theta(x) = \frac{1}{1+e^{-\theta^TX}}$ 带入到这样的代价函数中时，得到的代价函数将是一个非凸函数（non-convex function）。

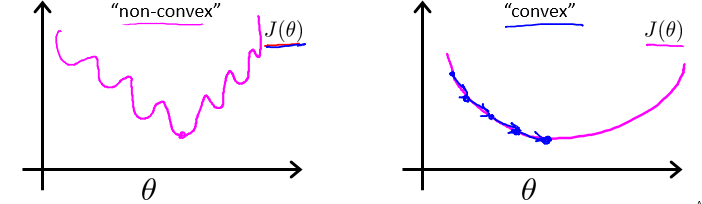
这意味着我们的代价函数有许多局部最小值，这将影响梯度下降算法寻找全局最小值。

线性回归的代价函数为：

$J(\theta)= \frac{1}{m}\sum^m_{i=1}\frac{1}{2}(h_\theta(x^{(i)})-y^{(i)})^2$

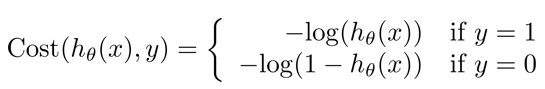
重新定义逻辑回归的代价函数为： $J(\theta)= \frac{1}{m}\sum^m_{i=1}Cost(h_\theta(x^{(i)}), y^{(i)})$ ，其中

$h_\theta(x)$ 与 $Cost(h_\theta(x), y)$ 之间的关系如下图所示：

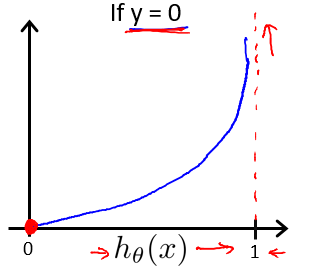
这样构建的 $Cost(h_\theta(x), y)$ 函数的特点是：

当实际的 y=1 且 $h_\theta(x)$ 也为1 时误差为 0，当 y=1 但 $h_\theta(x)$ 不为 1 时误差随着 $h_\theta(x)$ 的变小而变大；

当实际的 y=0 且 $h_\theta(x)$ 也为 0 时代价为 0，当 y=0 但 $h_\theta(x)$ 不为 0 时误差随着 $h_\theta(x)$ 的变大而变大。

将构建的 $Cost(h_\theta(x), y)$ 简化如下：
$Cost(h_\theta(x), y)=-y\times{log(h_\theta(x))}-(1-y)\times{log(1-h_\theta(x))}$ 带入代价函数得到： $J(\theta) = \frac{1}{m}\sum^m_{i=1}[-y^{(i)}log(h_\theta(x^{(i)}))-(1-y^{(i)}log(1-h_\theta(x^{(i)}))]$ 即： $J(\theta) = -\frac{1}{m}\sum^m_{i=1}[y^{(i)}log(h_\theta(x^{(i)}))+(1-y^{(i)}log(1-h_\theta(x^{(i)}))]$

牛刀小试

Todo: 补全下方的 cost 逻辑回归的代价函数

# 逻辑回归代价函数的Python代码实现：
import numpy as np
def cost(theta, X, y):
    theta = np.matrix(theta)
    X = np.matrix(X)
    y = np.matrix(y)
    first = np.multiply(-y, np.log(sigmoid(X * theta.T)))
    # Todo: 补全  second  
    second = np.multiply((1 - y), np.log(1 - sigmoid(X * theta.T)))
    return np.sum(first - second) / (len(X))


    
  