加法与标量乘法

矩阵的加法

行列数相等的才可以做加法，两个矩阵相加就是行列对应的元素相加。

我们看这个例子

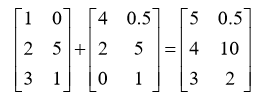
牛刀小试

import numpy as np
a = np.mat([[1,0],[2,5],[3,1]])
b = np.mat([[4,0.5],[2,5],[0,1]])
print ("a: \n",a, "\nb: \n",b)
print ("a+b: \n",a+b)  # a + b，矩阵相加
print("a-b:\n",a-b)  # a-b, 矩阵相减

a: 
 [[1 0]
 [2 5]
 [3 1]] 
b: 
 [[4.  0.5]
 [2.  5. ]
 [0.  1. ]]
a+b: 
 [[ 5.   0.5]
 [ 4.  10. ]
 [ 3.   2. ]]
a-b:
 [[-3.  -0.5]
 [ 0.   0. ]
 [ 3.   0. ]]

矩阵的标量乘法

矩阵和标量的乘法也很简单,就是矩阵的每个元素都与标量相乘。

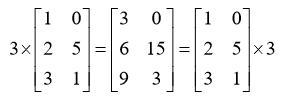
print ("a: \n",a)
print ("3*a: \n",3* a)  #矩阵标量乘法

a: 
 [[1 0]
 [2 5]
 [3 1]]
3*a: 
 [[ 3  0]
 [ 6 15]
 [ 9  3]]