梯度下降 - 特征缩放

• 梯度下降中的特征缩放: 确保特征具有相近的尺度

在我们面对多维特征问题的时候，我们要保证这些特征都具有相近的尺度，这可以帮助梯度下降算法更快地收敛。

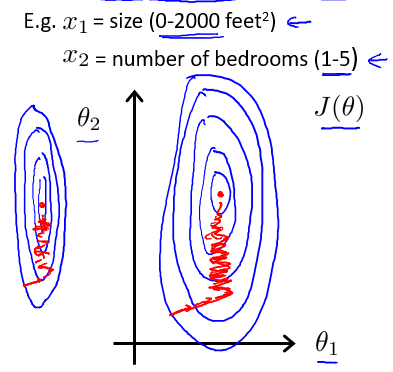
以房价问题为例，假设我们使用两个特征，房屋尺寸的值为 0-2000 平方英尺，而房间数量的值则是 0-5，以两个参数分别为横纵坐标，绘制代价函数的等高线图，能看出图像会显得很扁，梯度下降算法需要非常多次的迭代才能收敛。

为什么尺度相差很大的两个特征做梯度下降的时候, 会需要非常多次的迭代?

原因是, 回顾我们上一节的多变量梯度更新的公式(下图), 我们在更新每一个 ${\theta}$ 的时候, 使用的学习率 ${\alpha}$ 都是同一个值, 但是对于尺度差距很大的 ${\theta}$, 他们的梯度的尺度也会差距很大 (见下面的第一张等高线图), 可想而知, 如果我们要保证尺度较大的 ${\theta}$ 的下降速度, ${\alpha}$ 就会需要设置得很大, 这就会导致在小尺度的 ${\theta}$ 上来回波动很难向最低点靠拢, 也就是说满足了一个 ${\theta}$ 的学习效率就会导致另一个 ${\theta}$ 的学习效率变低, 想要满足所有 ${\theta}$ 上面的学习效率会变得很困难.

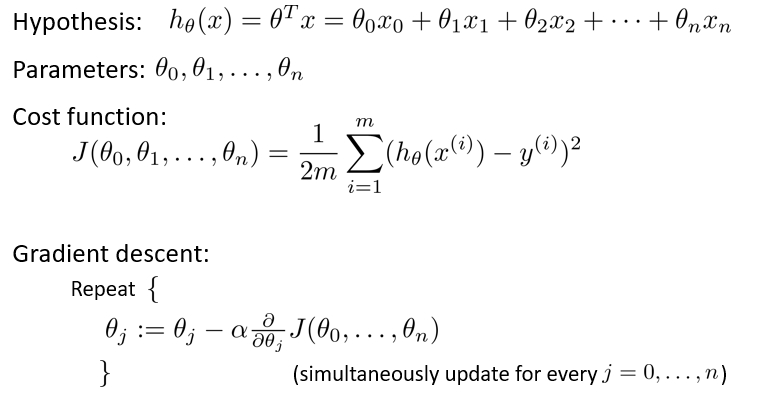
解决的方法是尝试将所有特征的尺度都尽量缩放到-1 到 1 之间。如图：

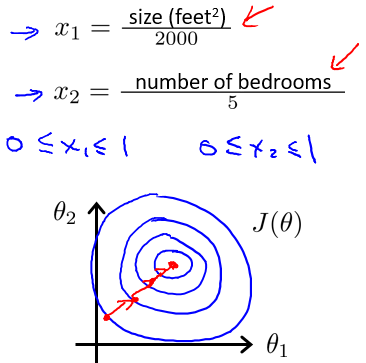
最简单的方法是令： $x_n = \frac{x_n - \mu_n}{s_n}$ 其中, $\mu_n$是平均值，$s_n$是标准差。

牛刀小试

Todo: $s_n$除了标准差,还能采用什么形式?

答：可以采用max-min的形式