正则化、偏差和方差
正则化系数的选择
选择正则化系数$\lambda$ 的值时也需要思考欠拟合和过拟合的问题。
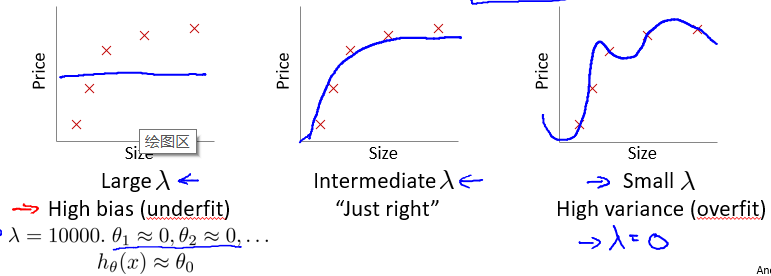
通常,我们选择一系列的想要测试的 λ 值,通常是 0-10 之间的呈现 2 倍关系的值(如:0,0.01,0.02,0.04,0.08,0.15,0.32,0.64,1.28,2.56,5.12,10 共 12 个)。 我们同样把数据分为训练集、交叉验证集和测试集。
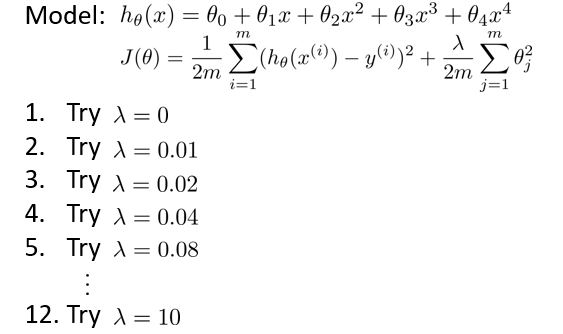
选择$\lambda$的方法为:
- 使用训练集训练出 12 个不同程度正则化的模型
- 用 12 模型分别对交叉验证集计算的出交叉验证误差
- 选择得出交叉验证误差最小的模型
- 运用步骤 3 中选出模型对测试集计算得出推广误差,我们也可以同时将训练集和交叉验证集模型的代价函数误差与$\lambda$的值绘制在一张图表上:
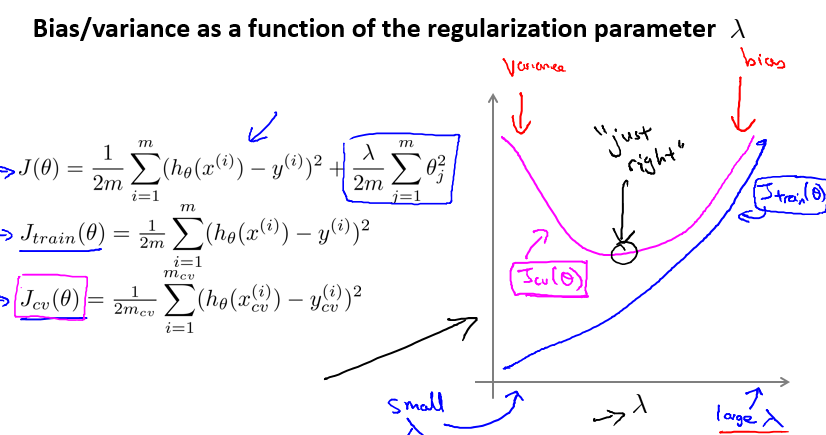
- 当$\lambda$较小时,训练集误差较小(过拟合)而交叉验证集误差较大
- 随着$\lambda$的增加,训练集误差不断增加(欠拟合),而交叉验证集误差则是先减小后增加
牛刀小试
Todo: 观察上图, 当$\lambda$较小时,训练集误差较小(过拟合)而交叉验证集误差较大 , 随着$\lambda$的增加,训练集误差不断增加(欠拟合),而交叉验证集误差则是先减小后增加, 这句话是正确的吗?
答:正确.