理解梯度下降
这一节我们主要学习以下内容
- 梯度下降的数学含义
- 梯度下降的更新过程
梯度下降算法如下: $\theta_{j} := \theta_{j} - \alpha\frac{\partial}{\partial{\theta_{j}}}J(\theta)$
描述:对$\theta$赋值,使得 $J(\theta)$按梯度下降最快方向进行,一直迭代下去,最终得到局部最小值。其中$\alpha$是学习率(learning rate),它决定了我们沿着能让代价函数下降程度最大的方向向下迈出的步子有多大。
对于这个问题,求导的目的,基本上可以说取这个红点的切线,就是这样一条红色的直线,刚好与函数相切于这一点,这条直线的斜率正好是这个三角形的高度除以这个水平长度。现在,这条线有一个正斜率,也就是说它有正导数,因此,我得到的新的 $\theta_{1}$,$\theta_{1}$更新后等于 $\theta_{1}$减去一个正数乘以$\alpha$。
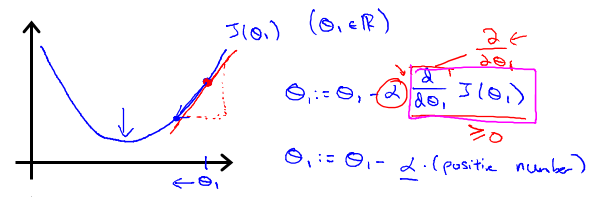
这就是梯度下降法的更新规则:
学习率$\alpha$的选择
让我们来看看如果$\alpha$太小或$\alpha$太大会出现什么情况:
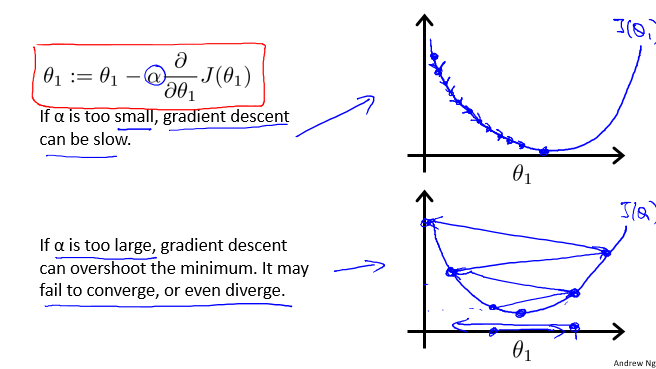
如果$\alpha$太小或$\alpha$太大会出现什么情况
- 如果$\alpha$太小了,即我的学习速率太小,可能会很慢,因为它会一点点挪动,它会需要很多步才能到达全局最低点。
- 如果$\alpha$太大,那么梯度下降法可能会越过最低点,下一次迭代又移动了一大步,越过一次,又越过一次,一次次越过最低点,直到你发现实际上离最低点越来越远,最终会导致无法收敛,甚至发散。
细节: 关于梯度下降的收敛
提问,如果我们预先把$\theta_{1}$放在一个局部的最低点,你认为下一步梯度下降法会怎样工作?
假设你将$\theta_{1}$初始化在局部最低点,它已经在一个局部的最优处。结果是局部最优点的导数将等于零,因为它是那条切线的斜率。这意味着你已经在局部最优点,它使得$\theta_{1}$不再改变,也就是新的 $\theta_{1}$等于原来的$\theta_{1}$,因此,如果你的参数已经处于局部最低点,那么梯度下降法更新其实什么都没做,它不会改变参数的值。这也解释了为什么即使学习速率$\alpha$保持不变时,梯度下降也可以收敛到局部最低点。 我们来看一个例子,这是代价函数$J(\theta)$。
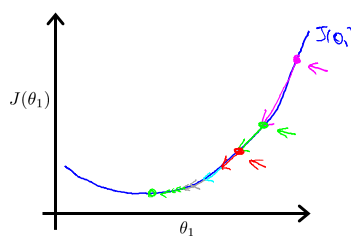
想找到它的最小值,首先初始化梯度下降算法(品红色的点),如果更新一步梯度下降,也许它会带我到这个绿色的点,因为这个点的导数是相当陡的。现在再更新一步,你会发现导数也即斜率,是没那么陡的。随着接近最低点,导数越来越接近零。自然地,用一个稍微跟刚才在那个品红点时比再小一点的一步,从绿色点到了新的红色点,更接近全局最低点了,这点的导数会比在绿点时更小。当再进行一步梯度下降时,导数项是更小的,更新的幅度就会更小。所以随着梯度下降法的运行,你移动的幅度会自动变得越来越小,直到最终移动幅度非常小,你会发现,已经收敛到局部极小值。
在梯度下降法中,当接近局部最低点时,梯度下降法会自动采取更小的幅度。这是因为当我们接近局部最低时,导数值会自动变得越来越小,在局部最低时导数等于零。所以梯度下降将自动采取较小的幅度,所以实际上没有必要再另外减小$\alpha$。
这就是梯度下降算法,你可以用它来最小化任何代价函数$J$,不只是线性回归中的代价函数$J$。