非监督学习介绍

典型的监督学习中，我们有一个有标签的训练集，我们的目标是找到能够区分正样本和负样本的决策边界需要据此拟合一个假设函数。

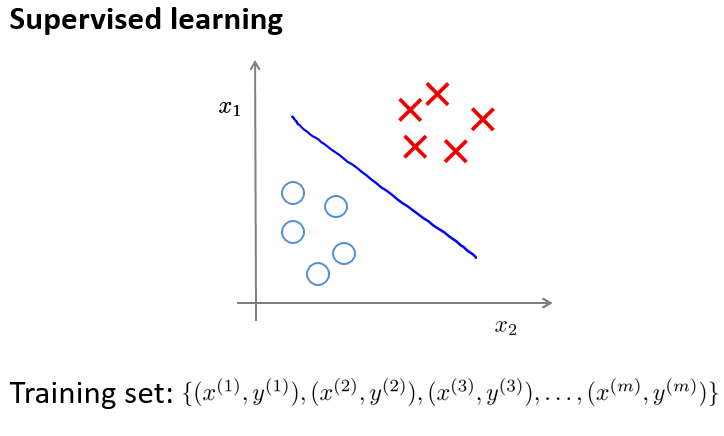
无监督学习中，数据没有附带任何标签：

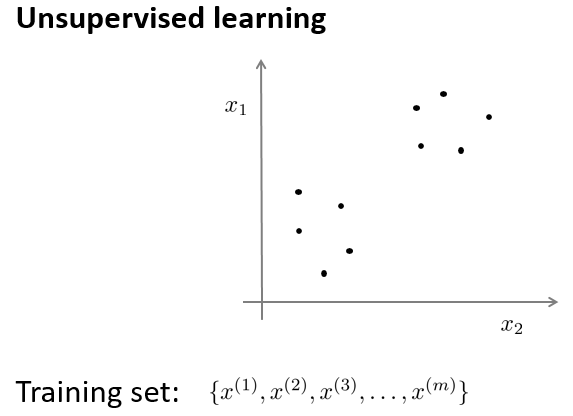
图上的数据看起来可以分成两个分开的点集（称为簇），一个能够找到我圈出的这些点集的算法，就被称为聚类算法。

聚类算法

聚类算法试图将数据集中的样本划分为若干个通常是不交集的子集，每个子集 称为一个簇（cluser）。形式化地说，假定样本集$D= {x_1,x_2,…,x_m}$包含m个无标记样本，每个样本$x_i$是一个n维特征向量，则聚类算法将样本D划分为k个不相交的簇${C_l|l=1,2,…,k}$，其中$C_{l^`}\cap_{l^` \neq l}C_l = \emptyset$且$D=\cup^k_{l=1}C_l$。相应地，我们用$\lambda_j \in {1,2,…,k}$表示样本$x_j$的“簇标记”（cluster label），即$x_ \in C_{\lambda_j}$。聚类结果也可以用包含m个元素的簇标记向量$\lambda = (\lambda_1,\lambda_2,…,\lambda_k)$表示。

牛刀小试

Todo: 你认为上面的无监督学习示意图中的样本点,可以聚为几类?

答：2类。