多元高斯分布

多元高斯分布

假使我们有两个相关的特征，而且这两个特征的值域范围比较宽，这种情况下，一般的高斯分布模型可能不能很好地识别异常数据。其原因在于，一般的高斯分布模型尝试的是去同时抓住两个特征的偏差，因此创造出一个比较大的判定边界。

下图中是两个相关特征，洋红色的线（根据$\varepsilon$的不同其范围可大可小）是一般的高斯分布模型获得的判定边界，很明显绿色的 x 所代表的数据点很可能是异常值，但是其$p(x)$值却仍然在正常范围内。多元高斯分布将创建像图中蓝色曲线所示的判定边界。

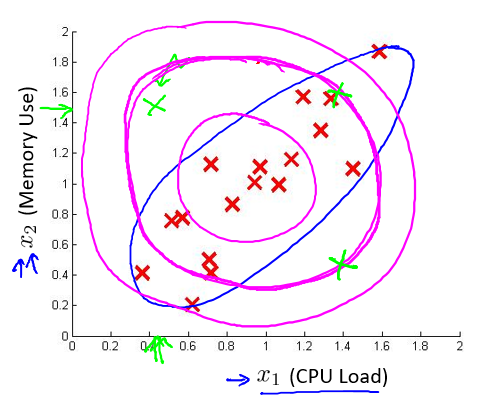
在一般的高斯分布模型中，我们计算$p(x)$的方法是： 通过分别计算每个特征对应的几率然后将其累乘起来，在多元高斯分布模型中，我们将构建特征的协方差矩阵，用所有的特征一起来计算$p(x)$。

构建特征的协方差矩阵，用所有的特征一起来计算$p(x)$。

我们首先计算所有特征的平均值，然后再计算协方差矩阵： $p(x)=\prod_{j=1}^n p(x_j;\mu_j,\sigma^2_j)=\prod_{j=1}^n \frac{1}{\sqrt{2\pi}\sigma_j}exp(-\frac{(x_j-\mu_j)^2}{2\sigma^2_j})$

$$均值: \mu_j = \frac{1}{m}\sum^m_{i=1}x^{(i)}_j$$ $$协方差: \Sigma = \frac{1}{m}\sum^m_{i=1}(x^{(i)}-\mu)(x^{(i)}-\mu)^T=\frac{1}{m}(X-\mu)^T(X-\mu)$$

注:其中$\mu$是一个向量，其每一个单元都是原特征矩阵中一行数据的均值。

最后我们计算多元高斯分布的$p(x)$:

$p(x) = \frac{1}{(2\pi)^{\frac{n}{2}}|\Sigma|^{\frac{1}{2}}}exp(-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu))$ 其中：

• $

  \Sigma

  $是定矩阵，在Octave 中用 det(sigma)计算

• $\Sigma^{-1}$是逆矩阵

下面我们来看看协方差矩阵是如何影响模型的：

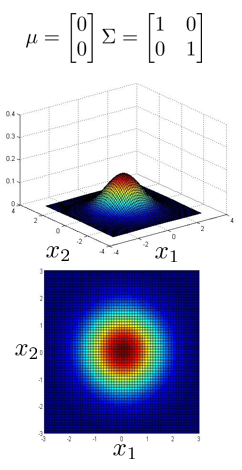
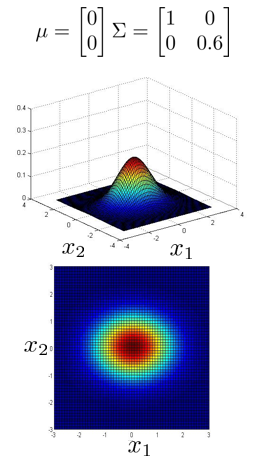
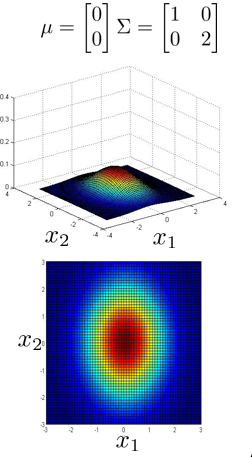
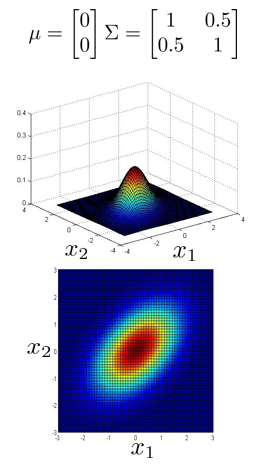
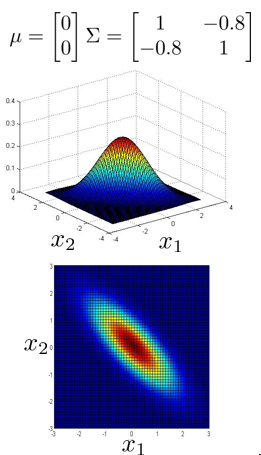
上图是 5 个不同的模型，从左往右依次分析：

1. 是一个一般的高斯分布模型
2. 通过协方差矩阵，令特征 1 拥有较小的偏差，同时保持特征 2 的偏差
3. 通过协方差矩阵，令特征 2 拥有较大的偏差，同时保持特征 1 的偏差
4. 通过协方差矩阵，在不改变两个特征的原有偏差的基础上，增加两者之间的正相关 性
5. 通过协方差矩阵，在不改变两个特征的原有偏差的基础上，增加两者之间的负相关 性

多元高斯分布模型与原高斯分布模型的关系

可以证明的是，原本的高斯分布模型是多元高斯分布模型的一个子集，即像上图中的第 1、2、3，3 个例子所示，如果协方差矩阵只在对角线的单位上有非零的值时，即为原本的高斯分布模型了。

原高斯分布模型和多元高斯分布模型的比较：

原高斯分布模型	多元高斯分布模型
不能捕捉特征之间的相关性,但可以通过将特征进行组合的方法来解决	自动捕捉特征之间的相关性
计算代价低，能适应大规模的特征	计算代价较高 训练集较小时也同样适用
	必须要有 m>n，不然的话协方差矩阵不可逆的，通常需要 m>10n 另外特征冗余也会导致协方差矩阵不可逆

原高斯分布模型被广泛使用着，如果特征之间在某种程度上存在相互关联的情况，我们 可以通过构造新新特征的方法来捕捉这些相关性。

如果训练集不是太大，并且没有太多的特征，我们可以使用多元高斯分布模型。