决策边界

逻辑回归模型中：

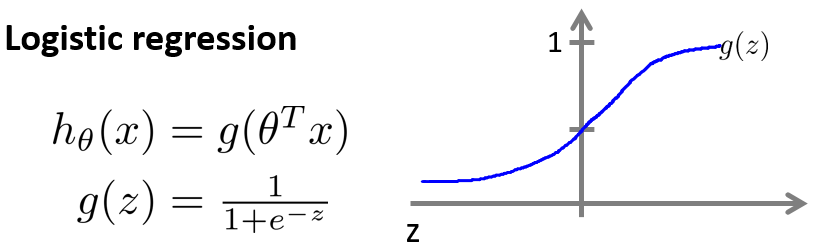
我们预测： 当 $h_\theta(x)$大于等于 0.5 时，预测 y=1。 当$h_\theta(x)$小于 0.5 时，预测 y=0 。

根据上面绘制出的 S 形函数图像，我们知道当

z=0 时 g(z)=0.5
z>0 时 g(z)>0.5
z<0 时 g(z)<0.5

又$z=\theta^Tx$ ，即：
$\theta^Tx$大于等于 0 时，预测 y=1
$\theta^Tx$小于 0 时，预测 y=0

现在假设我们有一个模型：

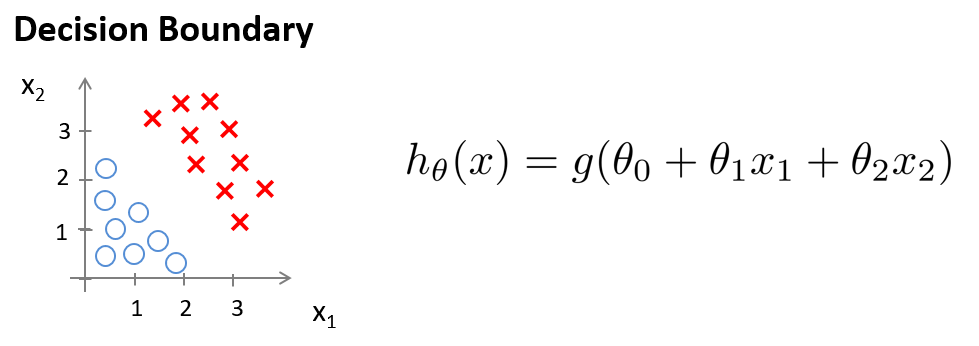
并且参数$\theta$是向量[-3 1 1]。 则当$-3 + x_1 + x_2$大于等于 0，将预测 y=1。

我们可以绘制直线$x_1+x_2 = 3$，这条线便是我们模型的分界线，将预测为 1 的区域和预 测为 0 的区域分隔开。

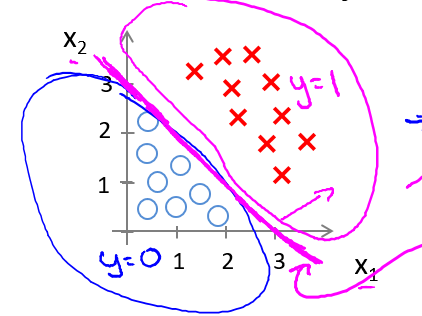
假使我们的数据呈现这样的分布情况，怎样的模型才能适合呢？

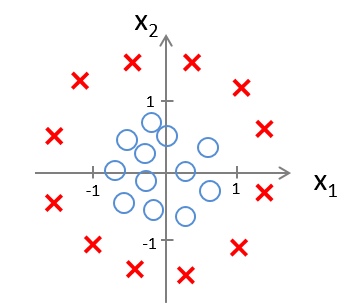
牛刀小试

Todo: 想一想,可以通过构造什么特征来分隔开上图的两类数据呢?

答：可以构造二次方特征