多变量梯度下降

与单变量线性回归类似，在多变量线性回归中，我们也构建一个代价函数，则这个代价 函数是所有建模误差的平方和，即： $J(\theta_{0}, \theta_{1}...\theta_{n}) = \frac{1}{2m}\sum_{i=1}^m(h_{\theta}(x^{(i)})-y^{(i)})^{2}$ 其中： $h_{\theta}(x) = \theta^TX = \theta_{0}x_{0} + \theta_{1}x_{1} + \theta_{2}x_{2} + ... + \theta_{n}x_{n}$ 我们的目标和单变量线性回归问题中一样，是要找出使得代价函数最小的一系列参数。

相应地，多变量线性回归的模型如下图：

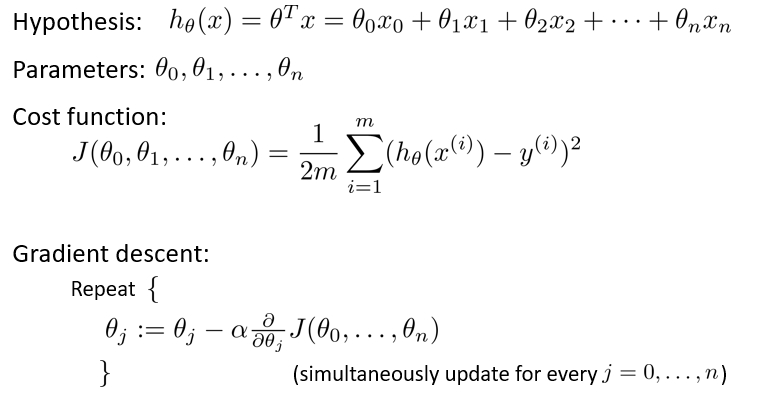
对梯度下降求导数后得到：

我们开始随机选择一系列的参数值，计算所有的预测结果后，再给所有的参数一个新的值，如此循环直到收敛。

实现多变量的 cost function

# 代价函数的python代码实现
def Cost(X, y, theta):
    inner = np.power(((X * theta.T) - y), 2)
    return np.sum(inner) / (2 * len(X))