K-Means 算法

K-均值是最普及的聚类算法，算法接受一个未标记的数据集，然后将数据聚类成不同的组。

K-均值算法的输入：

• K，聚类数目
• 无标签数据集

K-均值是一个迭代算法，假设我们想要将数据聚类成 n 个组，其方法为:

1. 选择 k 个随机的点，称为聚类中心（cluster centroids）；
2. 对于数据集中的每一个数据，按照距离 K 个中心点的距离，将其与距离最近的中心点关联起来，与同一个中心点关联的所有点聚成一类；
3. 计算每一个组的平均值，将该组所关联的中心点移动到平均值的位置；
4. 重复步骤 2-4 直至中心点不再变化。

用$\mu^1,\mu^2,…,\mu^k$来表示聚类中心，用$c^{(1)},c^{(2)},…c^{(m)}$来存储与第 i 个实例数据最近的聚 类中心的索引，K-均值算法的伪代码如下：

Repeat {     
for i = 1 to m     
c(i) := index (form 1 to K) of cluster centroid closest to x(i) 
 
for k = 1 to K 
μk := average (mean) of points assigned to cluster k 
} 

算法分为两个步骤，第一个 for 循环是赋值步骤，即：对于每一个样例 i，计算其应该属于的类。第二个 for 循环是聚类中心的移动，即：对于每一个类 k，重新计算该类的质心。

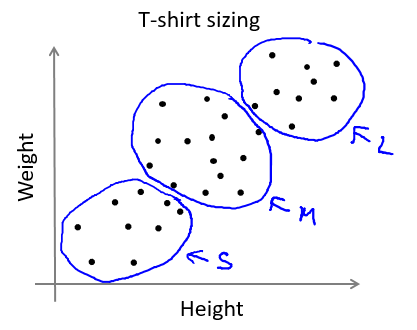
K-均值算法也可以很便利地用于将数据分为许多不同组，即使在没有非常明显区分的组群的情况下也可以。下图所示的数据集包含身高和体重两项特征构成的，利用 K-均值算法将数据分为三类，用于帮助确定将要生产的 T-恤衫的三种尺寸。

牛刀小试

Todo: 上面的问题,可以将 K 设置为其他值吗?

答：可以。