矩阵乘法的性质

  • 矩阵的乘法不满足交换律：$A×B≠B×A$
  • 矩阵的乘法满足结合律。即：$A×（B×C）=（A×B）×C$

单位矩阵

在矩阵的乘法中，有一种矩阵起着特殊的作用，如同数的乘法中的 1,我们称这种矩阵为单位矩阵．它是个方阵，一般用 I 或者 E 表示，本讲义都用 I 代表单位矩阵，从左上角到右下角的对角线（称为主对角线）上的元素均为 1 以外全都为 0。如：

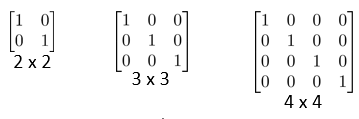
对于单位矩阵，有 $ AI = IA = A$。

import numpy as np

a = np.mat([[-1,2],[2,3]])
b = np.mat([[3,4],[4,5]])
print ("a: \n",a, "\nb: \n",b)


a: 
 [[-1  2]
 [ 2  3]] 
b: 
 [[3 4]
 [4 5]]

# 试试 a*b 和 b*a 是不是相同呢?
print ("a*b: \n",a*b)
print ("b*a: \n",b*a)


a*b: 
 [[ 5  6]
 [18 23]]
b*a: 
 [[ 5 18]
 [ 6 23]]

c = np.mat([[1,3],[2,4]])
print ("c: \n",c, )


c: 
 [[1 3]
 [2 4]]

# 试试 a*b*c 和 a*(b*c) 是不是相同呢?
print ("a*b*c: \n",a*b*c)
print ("a*(b*c): \n",a*(b*c))


a*b*c: 
 [[ 17  39]
 [ 64 146]]
a*(b*c): 
 [[ 17  39]
 [ 64 146]]