高级优化技巧
- 逻辑回归的高级优化算法
- 如何使用这些算法
通过一些高级优化算法和一些高级的优化概念,能够使梯度下降进行逻辑回归的速度大大提高,而这也将使算法更加适合解决大型的机器学习问题,比如,我们有数目庞大的特征量。
现在我们换个角度来看什么是梯度下降,我们有个代价函数$J(\theta)$ ,而我们想要使其最小化,那么我们需要做的是编写代码,当输入参数 $\theta$时,它们会计算出两样东西:$J(\theta)$以及 $J=0,1,…,n$ 时的偏导数项。

假设我们已经完成了可以实现这两件事的代码,那么梯度下降所做的就是反复执行这些更新。 另一种考虑梯度下降的思路是:我们需要写出代码来计算$J(\theta)$和这些偏导数,然后把这些插入到梯度下降中,然后它就可以为我们最小化这个函数。
计算代价函数$J(\theta)$和偏导数项 $\frac{\partial}{\partial \theta_j}J(\theta)$可以用其他方法:Conjugate gradient,共轭梯度法 BFGS (变尺度法) 和 L-BFGS (限制变尺度法) ,使用比梯度下降更复杂的算法来最小化代价函数。这两种算法的具体细节超出了本门课程的范畴。
Conjugate gradient,共轭梯度法 BFGS (变尺度法) 和 L-BFGS (限制变尺度法) 这三种算法的优点:
- 不需要手动选择学习率 α。
- 收敛更快。
缺点:
- 过于复杂
一个例子
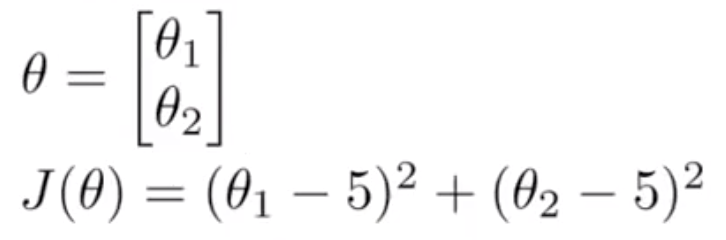
比方说,一个含两个参数的问题,这两个参数是$\theta_0$ 和 $ \theta_1 $ ,因此,通过这个代价函数,你可以得到 $\theta_1$和$\theta_2$的值,如果你将$J(\theta)$最小化的话,那么它的最小值将是$\theta_1=5$, $\theta_2=5$。
代价函数$J(\theta)$的导数推出来就是这两个表达式:
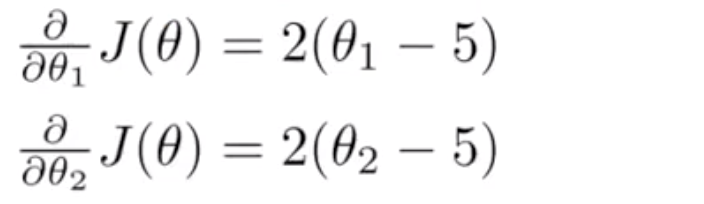
如果我们不知道最小值,但你想要代价函数找到这个最小值,是用比如梯度下降这些算法,但最好是用比它更高级的算法,你要做的就是运行一个像这样的 Octave 函数:
function [jVal, gradient]=costFunction(theta)
jVal=(theta(1)-5)^2+(theta(2)-5)^2;
gradient=zeros(2,1);
gradient(1)=2*(theta(1)-5);
gradient(2)=2*(theta(2)-5);
end
这样就计算出这个代价函数,函数返回的第二个值是梯度值,梯度值应该是一个 2×1的向量,梯度向量的两个元素对应这里的两个偏导数项,运行这个 costFunction 函数后,你就可以调用高级的优化函数,这个函数叫 fminunc,它表示 Octave 里无约束最小化函数。
调用它的方式如下:
options=optimset('GradObj','on','MaxIter',100);
initialTheta=zeros(2,1);
[optTheta, functionVal, exitFlag] = fminunc(@costFunction, initialTheta, options);
你要设置几个 options,这个 options 变量作为一个数据结构可以存储你想要的 options,所以 GradObj 和 On,这里设置梯度目标参数为打开(on),这意味着你现在确实要给这个算法提供一个梯度,然后设置最大迭代次数,比方说 100,我们给出一个 θ 的猜测初始值,它是一个 2×1 的向量,那么这个命令就调用 fminunc,这个@符号表示指向我们刚刚定义的costFunction 函数的指针。如果你调用它,它就会使用众多高级优化算法中的一个,当然你也可以把它当成梯度下降,只不过它能自动选择学习速率 α,你不需要自己来做。然后它会尝试使用这些高级的优化算法,就像加强版的梯度下降法,为你找到最佳的 θ 值。