高斯分布的异常检测算法
高斯分布的异常检测算法
对于给定的数据集$x^{(1)}, x^{(2)},…,x^{(m)}$,我们要针对每一个特征计算$\mu$和$\sigma^2$的估计值。
一旦我们获得了平均值和方差的估计值,给定新的一个训练实例,根据模型计算 $p(x)$:
当 $p(x)<\varepsilon$时,为异常。
下图是一个由两个特征的训练集,以及特征的分布情况:
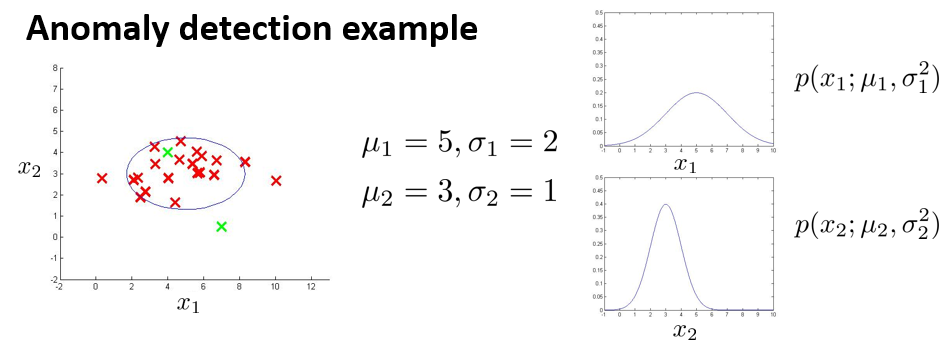
下面的三维图表表示的是密度估计函数,z 轴为根据两个特征的值所估计$p(x)$值:
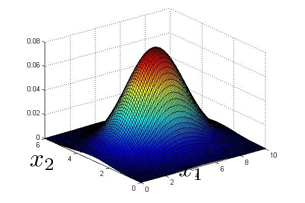
我们选择一个 $\varepsilon$,将 $p(x)=\varepsilon$ 作为我们的判定边界,当 $p(x)>\varepsilon$ 时预测数据为正常数据,否则为异常数据。
在这段视频中,我们介绍了如何拟合$p(x)$,也就是 x 的概率值,以开发出一种异常检测算法。同时,在这节课中,我们也给出了通过给出的数据集拟合参数,进行参数估计,得到参数$\mu$和$\sigma$,然后检测新的样本,确定新样本是否是异常。