这节我们主要学习
- 回顾一下结构化学习的模型
- 可分离的情况
- 不可分离的情况
- 结构化支持向量机
- 切割平面法
- 多分类支持向量机
1. 回顾
1.1 结构化学习
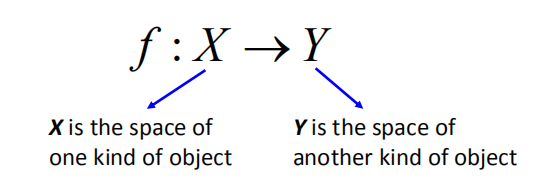
- 我们需要一个功能更强大的函数$f$
- 输入和输出都是具有结构的对象
- 对象:序列,列表,树,边界框$…$
1.2 统一框架
 分为 Training 和 Testing 两个部分。
分为 Training 和 Testing 两个部分。
1.3 三个问题
- $F(x,y)$ 长什么样子
- 怎样求解 arg max 问题
- 如何找到$F(x,y)$

1.4 实例任务
 在本节课程中,我们使用目标检测的例子进行讲解;
在本节课程中,我们使用目标检测的例子进行讲解;
但我们今天学习到的内容同样可以用作其他任务.
**问题1:估算**假设 $F(x,y)$ 是线性的
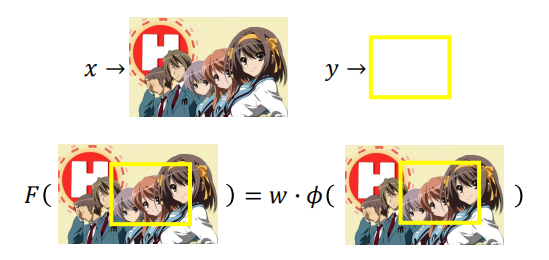
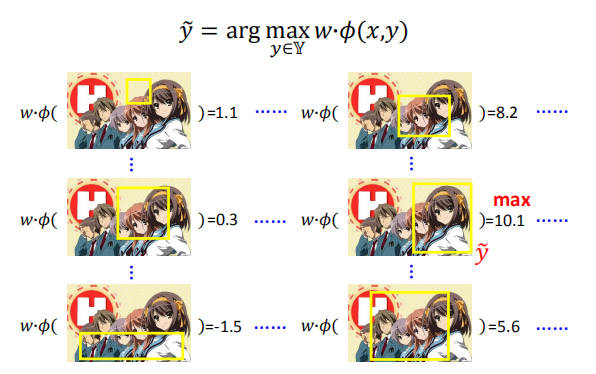 找到使 $F(x,y)$ 最大的 $\tilde y$
找到使 $F(x,y)$ 最大的 $\tilde y$
求解 $\tilde y$ 的方法
- 目标检测
- 分支定界算法
- 选择性搜索
- 序列标记
- 维特比算法
-
算法依赖于 $\phi (x,y)$
- 遗传算法
 数据集对应的 $F(x,y)$ 应该是最大的
数据集对应的 $F(x,y)$ 应该是最大的
接下来我们忽略问题 1 和问题 2,直接关注于问题 3。
2. 可分离的情况
假设:可分离
- 权重向量 $\hat w$ 存在,使得所有红色标记点的乘积的值大于其余蓝色点的乘积的值加上 $\delta$(红色代表是正确的,蓝色代表是错误的)
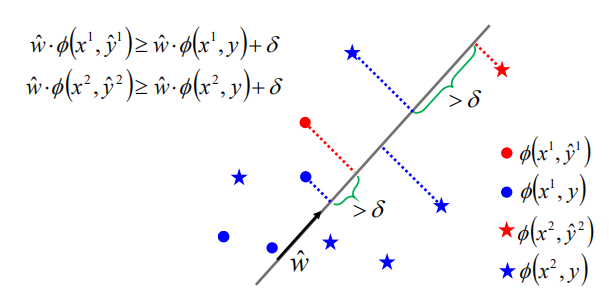
2.1 结构感知器
 当 $w$ 不再更新的时候,算法结束。
当 $w$ 不再更新的时候,算法结束。
2.2 数学证明
在可分离的案例中,为了获得 $\hat w$,最多需要更新 $(\frac {R} {\delta})^2$ 次
$\delta:$边距;
$R:$ $\phi(x,y)$ 和 $\phi (x,y’)$ 之间的最大距离
当看见一个错误的时候,$w$ 进行更新
 在可分离的案例中,我们不是一般性地设 $\hat w$ 的长度为 1(若 $\hat w$ 的长度不为 1,但是对其标准化之后,这依然是一个可分离的问题)
在可分离的案例中,我们不是一般性地设 $\hat w$ 的长度为 1(若 $\hat w$ 的长度不为 1,但是对其标准化之后,这依然是一个可分离的问题)

随着 $k$ 的增加,$\hat w$ 和 $w^k$ 之间的夹角 $\rho_k$ 越来越小。
$cos\rho_k= \frac{\hat w}{\|\hat w\|}$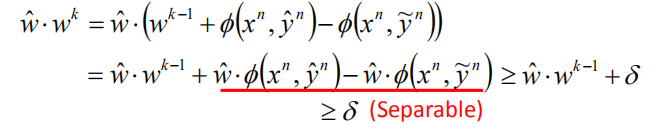 如图,分子 $\hat w \cdot w^k$ 的值随着 $k$ 的增大越来越大
如图,分子 $\hat w \cdot w^k$ 的值随着 $k$ 的增大越来越大
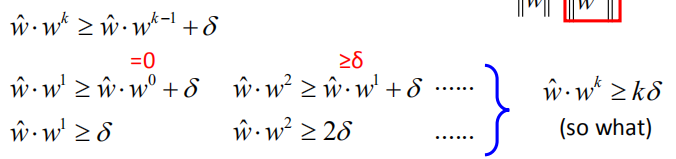 分母,我们之前假设 $\hat w$ 的长度为1,确定 $w^k$ 的长度即可。
分母,我们之前假设 $\hat w$ 的长度为1,确定 $w^k$ 的长度即可。

夹角的余弦值为:
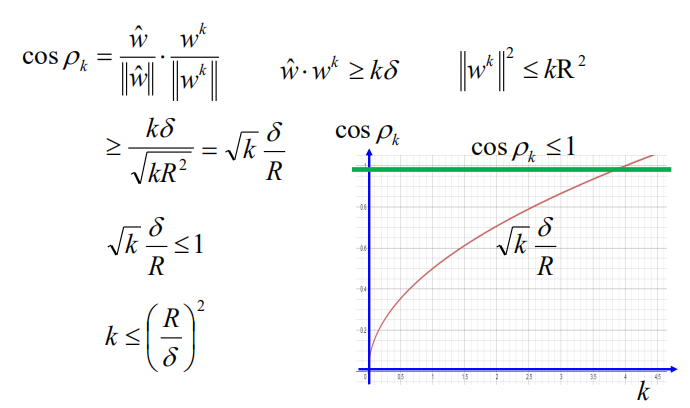 余弦值的下界会不断增加,但余弦值不会超过1;
余弦值的下界会不断增加,但余弦值不会超过1;
所以$k$要小于等于$(\frac {R} {\delta})^2$,即最多需要更新$(\frac {R} {\delta})^2$次
如何让训练更快?
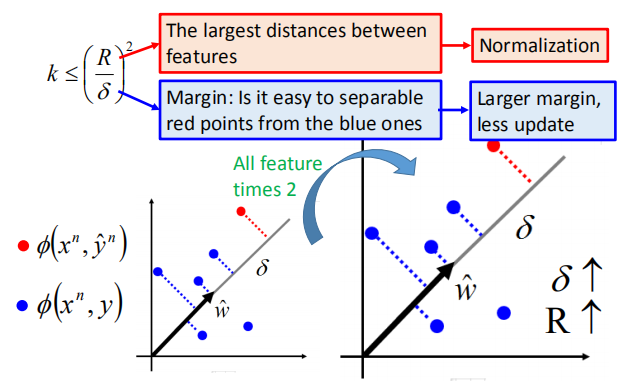 当边距越大的时候,训练越快
当边距越大的时候,训练越快
3. 不可分离的情况
当数据不能完全分离的时候,我们依旧可以判断某些权重比其他的权重更好。
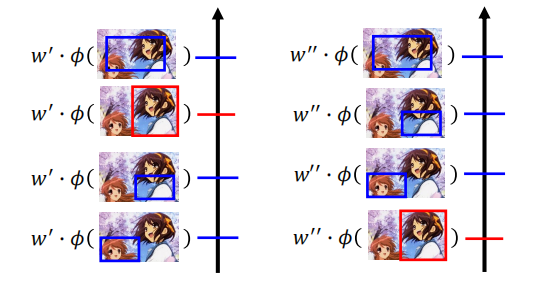
定义一个损失 $C$ 来估计权重 $w$ 到底有多差,我们需要选择最小化损失 $C$ 的 $w$
损失的定义如下:
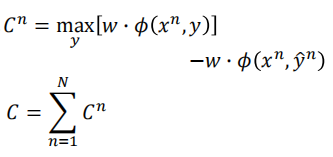 用所有可能y得到的最大值减去训练样本对应的值,得到最后的损失函数的值(都是大于等于 0 的)。
用所有可能y得到的最大值减去训练样本对应的值,得到最后的损失函数的值(都是大于等于 0 的)。
3.1 随机梯度下降
$C^n=max[w\cdot \phi (x^n,y)]-w\cdot \phi (x^n,\hat y^n)$
由于存在 $max$ 函数,当 $w$ 在不同的区域的时候,$y$ 的取值是不一样的
计算梯度:
 随机选取一个训练数据,确定 $y$ 在 $w$ 的哪个区域中,然后采用梯度下降法进行更新。
随机选取一个训练数据,确定 $y$ 在 $w$ 的哪个区域中,然后采用梯度下降法进行更新。
当 $\eta$=1 的时候,我们实际上是在处理结构化感知器
3.2 考虑误差
 之前,我们并没有考虑不正确的 $y$ 的差异性,实际上右边的情况,比左边的要好很多。
之前,我们并没有考虑不正确的 $y$ 的差异性,实际上右边的情况,比左边的要好很多。
所以,我们需要考虑不正确的 $y$ 之间的好坏。
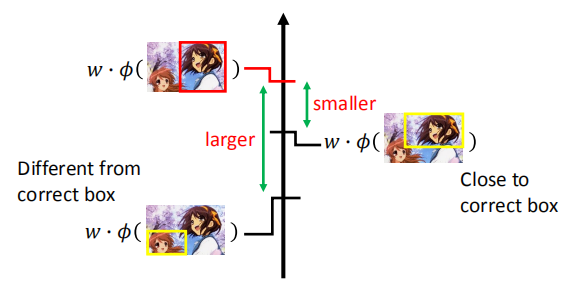
定义误差函数:
$\Delta (\hat y,y)$:y 和 $\hat y$ 之间的误差(是大于 0 的)
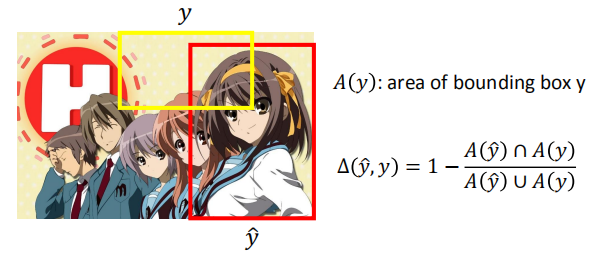 当 $\hat y$ 和 $y$ 之间完全没有重叠的时候,误差最大为 1;
当 $\hat y$ 和 $y$ 之间完全没有重叠的时候,误差最大为 1;
当 $\hat y$ 和 $y$ 之间重合的时候,误差为 0。
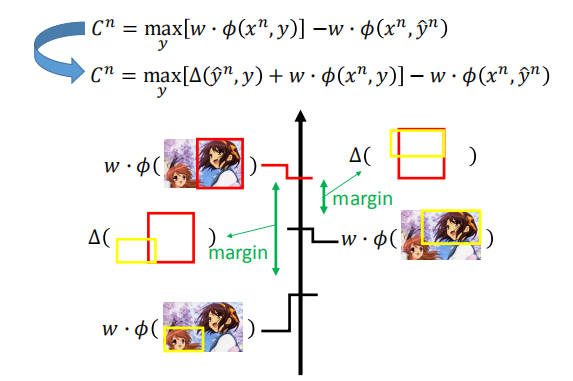
 我们需要找到新的函数的最大值,因此我们需要设计一个较好的误差,让这个最大值能够解出来;
我们需要找到新的函数的最大值,因此我们需要设计一个较好的误差,让这个最大值能够解出来;
其余部分与改良前的算法没有什么区别。
- 最小化新的损失函数是最小化训练集上误差的上限
 $C’$ 误差可能出现阶梯状的情况,影响梯度更新;我们使用新的损失函数 $C$ 来代替;
$C’$ 误差可能出现阶梯状的情况,影响梯度更新;我们使用新的损失函数 $C$ 来代替;
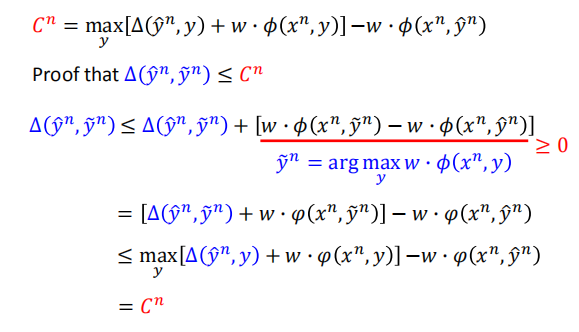

3.3 正则化
当训练集数据和测试集数据属于不同的分布的时候,$w$ 接近0可以消除 mismatch 的影响。
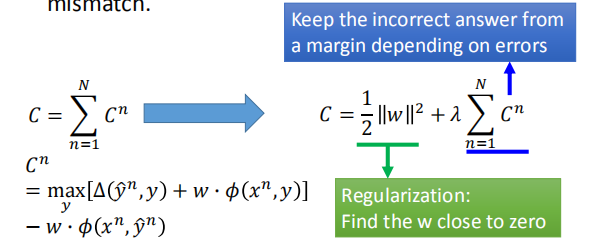 原始的损失函数可以让错误的答案与正确答案之间保持间距;
原始的损失函数可以让错误的答案与正确答案之间保持间距;
正则化能够让 $w$ 接近 0。

4. 结构化支持向量机
我们需要找到 $w$,使损失函数达到最小。
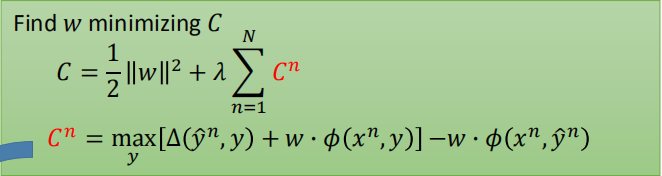
由于我们需要最小化损失函数,所以上式和下面的不等式相等(将 $w \cdot \phi(x^{n},\hat y^{n})$ 移到等式左边)。
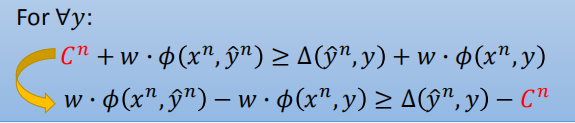
我们将 $C^n$ 称为松弛变量,使用 $\epsilon$ 来表示。

对于任意的 $y$ 不等于 $\hat y$,上述不等式均成立。
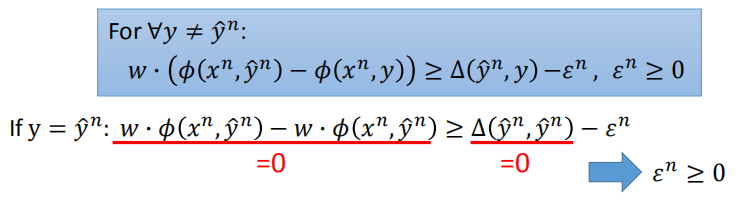
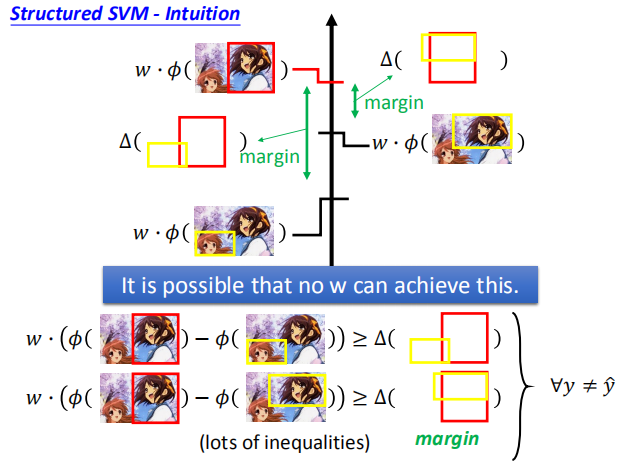 我们可能会遇到不存在 w 使 w 与 $\phi (x^n,\hat y^n)$ 的乘积满足 margin 的要求,
我们可能会遇到不存在 w 使 w 与 $\phi (x^n,\hat y^n)$ 的乘积满足 margin 的要求,
所以,可以使用松弛变量来减小不等式的约束。
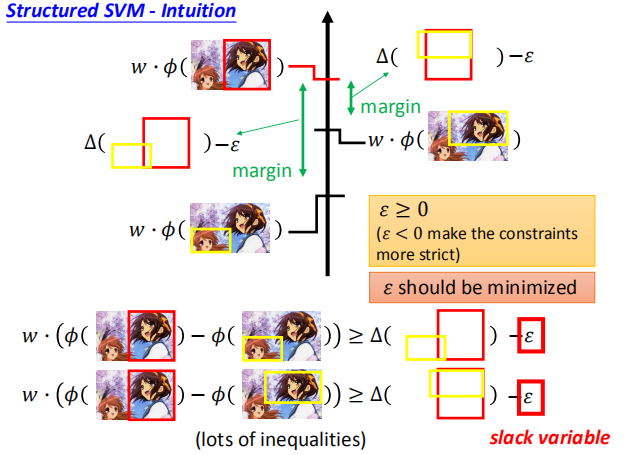 不让不等式的约束无限减小,$\epsilon$ 应该竟可能的小。
不让不等式的约束无限减小,$\epsilon$ 应该竟可能的小。
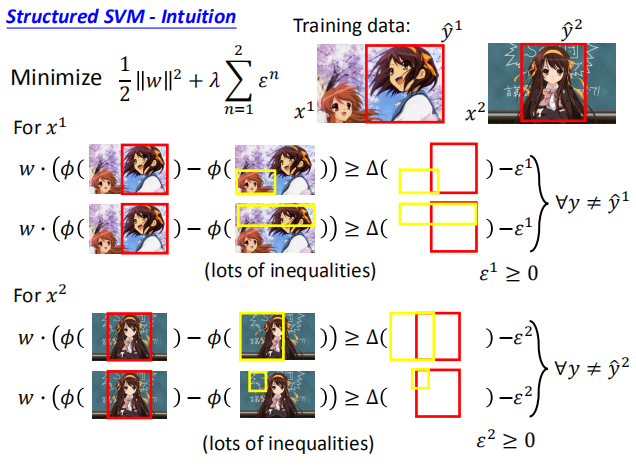 在满足不等式的情况下,我们希望 $\epsilon$ 的和最小
在满足不等式的情况下,我们希望 $\epsilon$ 的和最小
 我们在最小化损失函数同时,需要满足上面的约束条件。
我们在最小化损失函数同时,需要满足上面的约束条件。
$y$ 的取值有成千上万中可能,当限制条件这么多情况下,我们应该如何求解最小值?
5. 切割平面算法
我们需要在满足下面约束条件的情况下,求得损失函数的最小值。

根据不同的约束条件,我们可以将曲面分成不同的区域,求得对应区域的最小值。
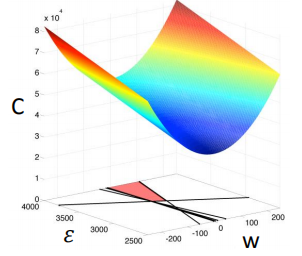
 不同的约束条件将参数空间分割成不同的部分。
不同的约束条件将参数空间分割成不同的部分。
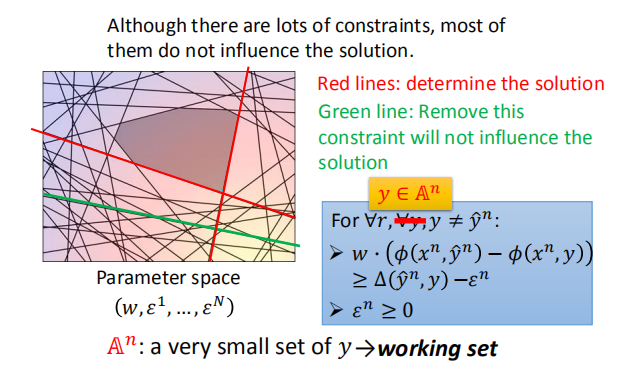 尽管这里众多的约束条件,但是真真起作用的还是红色线条表示的部分。
尽管这里众多的约束条件,但是真真起作用的还是红色线条表示的部分。
- 元素被不断迭代地选入工作集
 每次迭代之前,都会有一个工作集,计算 $w$,
每次迭代之前,都会有一个工作集,计算 $w$,
然后选择合适的元素加入工作集,进行下一次迭代
- 将元素逐渐添加到工作集中
 我们初始化工作集为空集,计算得到(二次规划问题)一个 $w$,
我们初始化工作集为空集,计算得到(二次规划问题)一个 $w$,
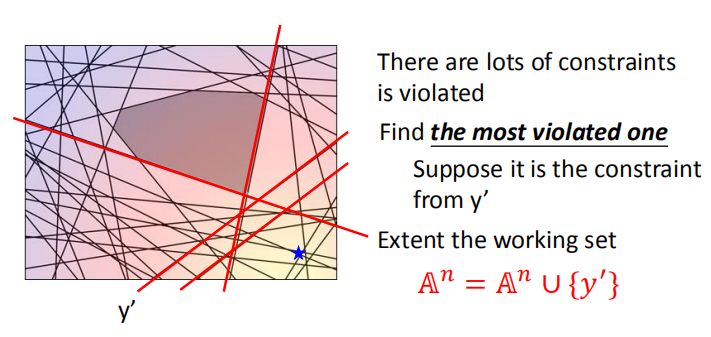 然后找到最不满足当前约束条件的元素加入到工作集中,不断迭代。
然后找到最不满足当前约束条件的元素加入到工作集中,不断迭代。
- 找到最不满足约束的元素
当$w$和$\epsilon$确定之后,如何寻找最不满足约束条件的 $y$:


-
初始化每个训练集数据的工作集为空;
- 不断循环直到每个工作集不再改变:
- 在相应的工作集下,利用二次规划求解 $w$
- 对于每一个训练数据,找到最违反规则的 y
-
将该元素加入到相应的工作集进行更新
- 返回 $w$
6.多分类支持向量机
我们可以用结构化学习的框架来处理多分类问题:
- 评估:
- 如果有K类,那么我们有K个权重向量{$w^1,w^2,…,w^K$}

- 推理:
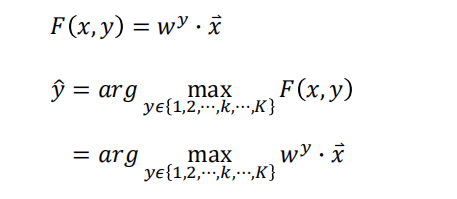 类的数量通常很小,所以我们可以枚举它们。
类的数量通常很小,所以我们可以枚举它们。
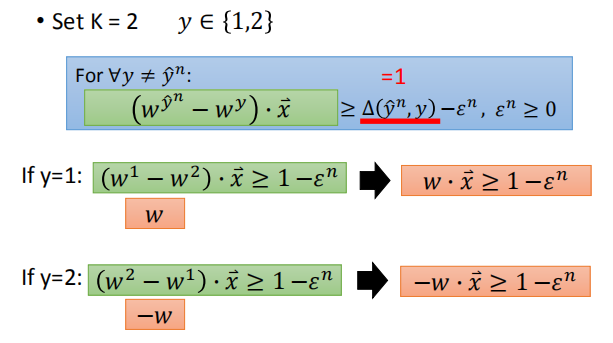
- 训练
由于约束条件比较少,我们直接穷举即可。
 当两个类别差别较大时,我们可以将 $\Delta$ 的值设置的较大
当两个类别差别较大时,我们可以将 $\Delta$ 的值设置的较大
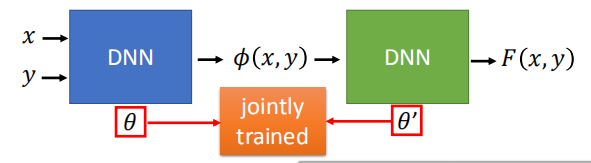
7. 深度神经网络与结构化支持向量机
前面我们学习的结构化模型都是线性的,功能不是很强大;
- 使用深度神经网络生成较为强大的模型,
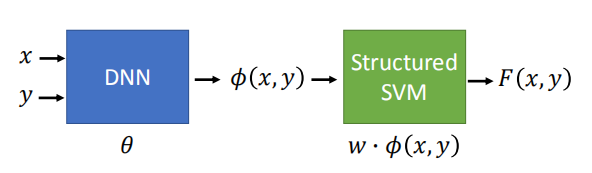
- 将结构化支持向量机和深度神经网络一起训练
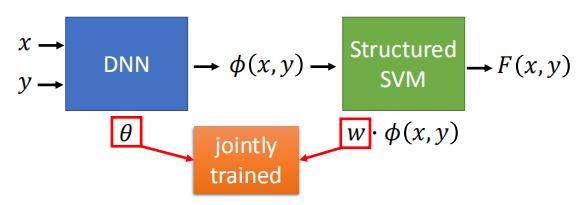
- 将结构化支持向量机用深度神经网络代替,变成更深的神经网络