这一节我们主要学习
- 深度学习
- 神经网络
- 损失函数
- 反向传播
1.深度学习
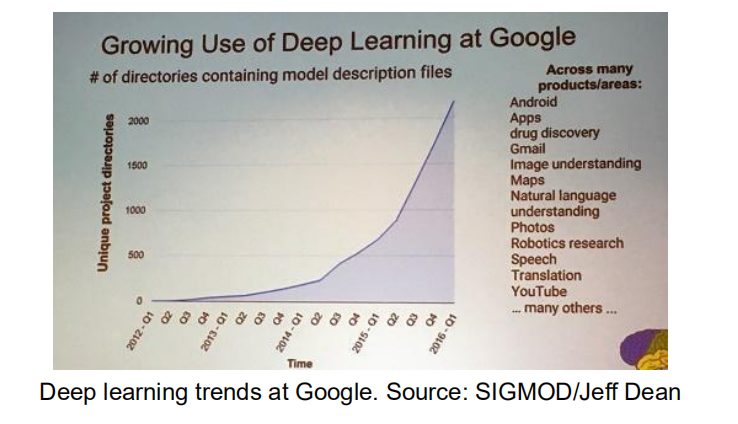
1.1 深度学习的发展趋势
深度学习吸引了很多的关注,并且在很多领域都有应用:
1.2 深度学习的发展历史

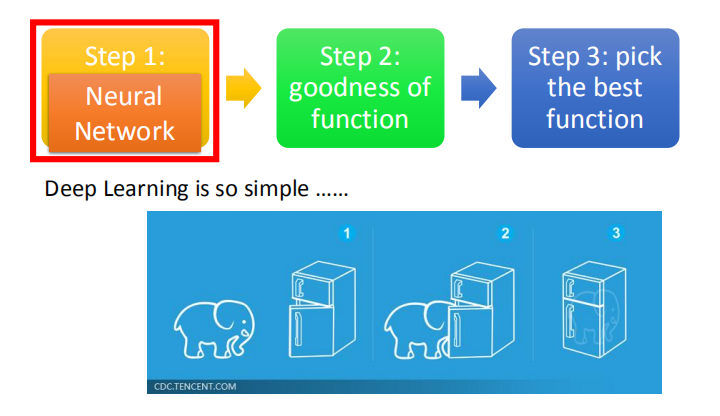
1.3 深度学习的三个步骤
2.神经网络 – 深度学习的第一步
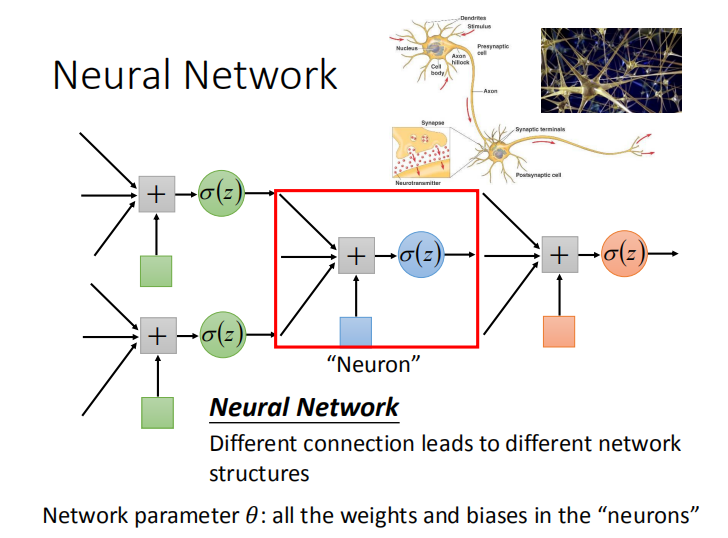
2.1 什么是神经网络
- 神经网络:神经元间的不同连接组成不同的网络结构。
- 网络参数 $\theta$:所有神经元的权重和偏差。
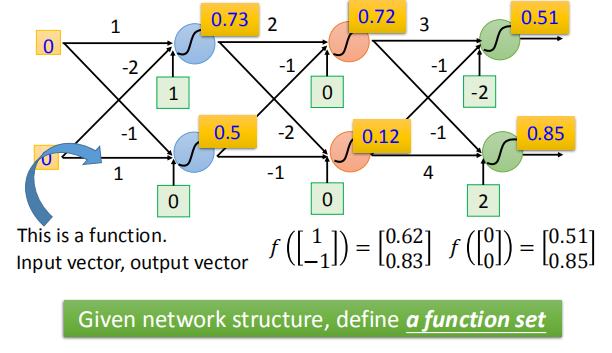
2.2 全连接前馈网络
- 全连接:每一层的神经元之间全部两两连接;前馈:传递的方向由后往前
- 将神经元以全连接的方式连接起来,不确定网络参数(Network parameter),相当于确定了一个函数集 - 神经网络。
- 确定网络参数相当于从函数集中确定了一个函数,每输入一个向量都会有一个输出的向量与之对应。
- 网络参数应该是从训练数据中学出来的
- 一般而言,每一层神经元的个数和层数都是不确定的。隐藏层的层数对应 Deep 的概念。
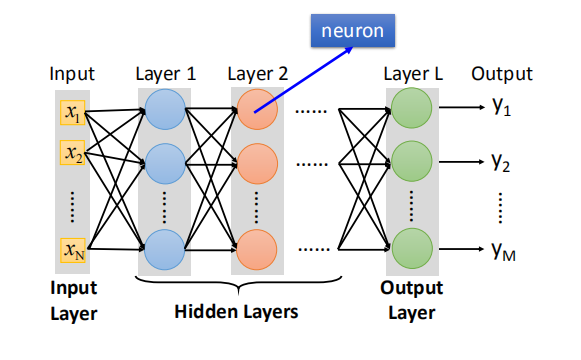
- 随着隐藏层数目增加,网络的错误率减少,且层间连接方式会发生变化,使用非全连接的其他方式。
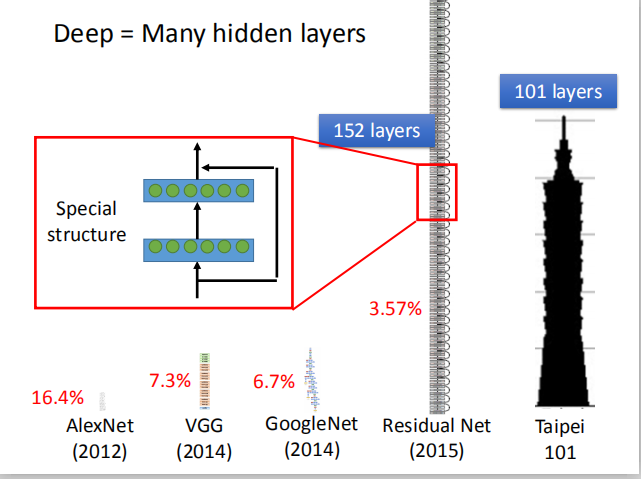
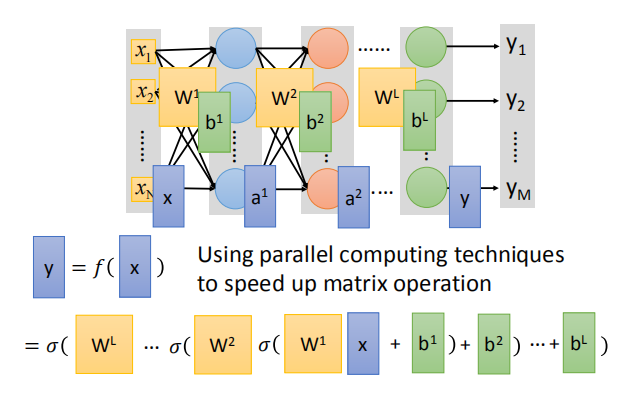
- 调用 GPU 利用并行计算技术加快矩阵运算:
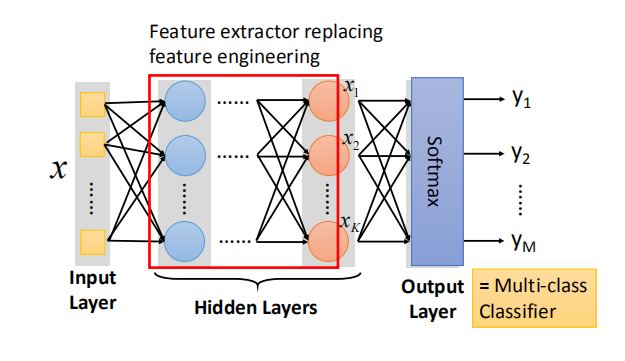
- 全连接前馈网络的隐藏层起到特征提取的作用,输入的特征经过隐藏层之后转换成一组新的特征,取代之前的手动特征转换工程。
- 输出层相当于一个多分类器,将提取后的特征进行分类。因为多分类器要通过 Softmax 函数,所以在输出层也会加上 Softmax 函数。
2.3 应用例子
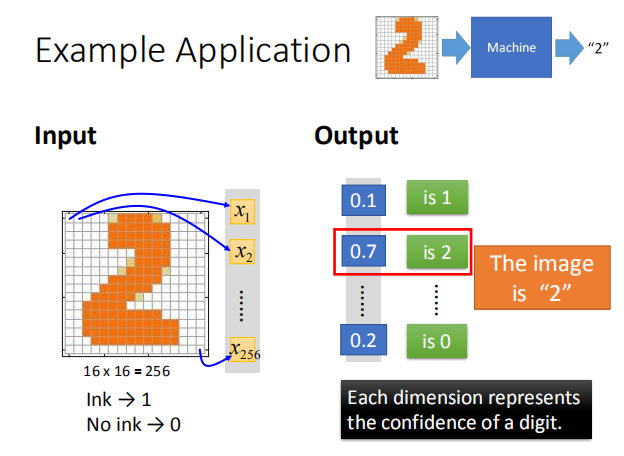
- 输入一张手写数字的图片,输出这张图片对应的数字:
- 假设输入图片的解析度为 16 * 16,那么它就有 256 个像素,对应一个 256 维的向量;
- 输出是一个 10 维的向量,每一个维度代表对应数字的几率。
- 要实现手写数字识别,我们所需要的就是一个函数,即神经网络。
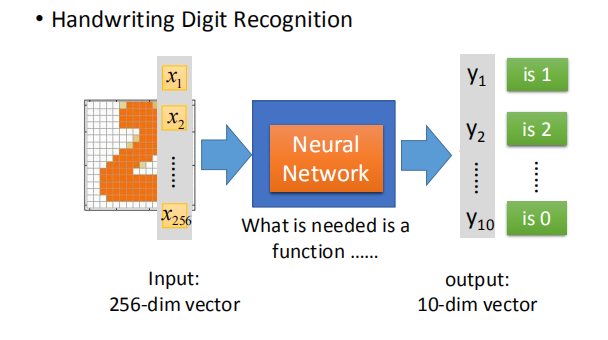
- 那么怎么确定这个网络呢?其实,这里对网络的限制只是输入是一个 256 维的向量,输出是一个 10 维的向量,对中间的网络结构并没有任何限制。
- 假设我们确定用全连接前馈网络,也就是确定了一个函数集,接下来还需要用梯度下降算法找到表现最好的那个函数。
- 但是一个不好的网络结构可能不包含一个表现好的函数,所以我们需要设计网络结构以保证表现最好的那个函数在我们的函数集里。
-
那么如何设计网络结构呢?
-
如何确定网络的层数和每一层有多少神经元?
答:试错法(经验) + 直觉
-
网络结构能否自动学习?
答:可以,比如进化人工神经网络。
-
我们能否自己设计网络结构?
答:可以,比如卷积神经网络(CNN)。
3.损失函数 – 深度学习的第二步和第三步
- 定义一个函数的好坏–损失函数
- 对于一个训练数据,我们可以计算函数结果和实际数据的交叉熵
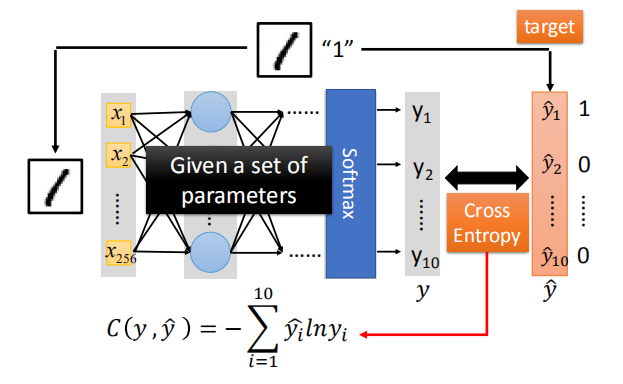
- 整个网络的损失函数:$L=\sum_{n=1}^N C^n$ ,即所有训练数据的交叉熵的和
- 接下来,我们需要在函数集中确定一个函数使总损失达到最小,即确定神经网络的参数 $θ^*$ 使损失函数最小
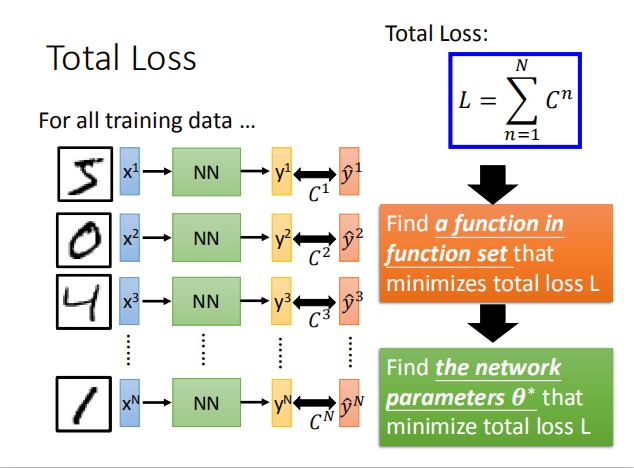
- 给定一组参数的初始值,计算梯度,根据学习率更新参数值,循环往复,直到找到一组好的参数。这就是机器在深度学习中的学习过程。
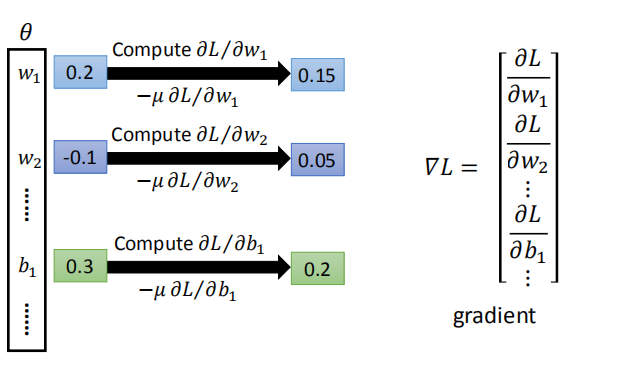

4.反向传播
- 反向传播:计算神经网络中偏微分的有效方式。

5.结束语
-
为什么要用深度学习?越深越好?
-
普遍性定理:只要有足够多的神经元,任何连续函数 $f: R^N \rightarrow R^M$ ,都能够被一个仅有一层隐藏层的网络实现。
