这一节我们主要学习
- 流形学习(Manifold Learning)
- 局部线性嵌入(Locally Linear Embedding (LLE))
- 拉普拉斯特征映射(Laplacian Eigenmaps)
- T-distributed Stochastic Neighbor Embedding (t-SNE)
1. 流形学习
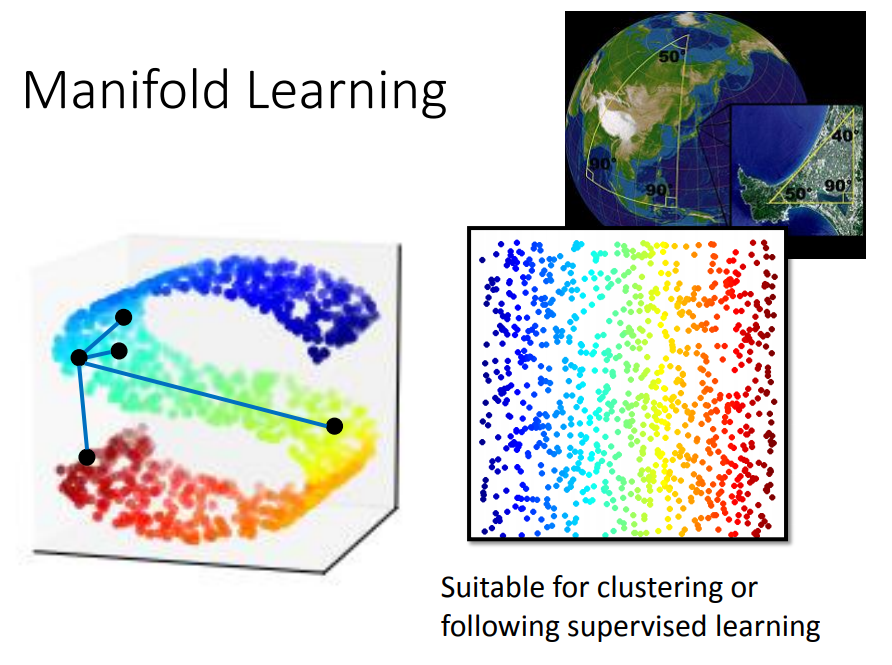
我们要做的是非线性的降维,数据是分布在低维空间里面,只是被扭曲到了高维空间。
比如地球的表面是一个二维平面,但是被塞到一个三维空间中。
流行学习就是把 S 型摊平,将高维空间内的低维数据展开,这样才能计算点对点的距离。
2. 局部线性嵌入
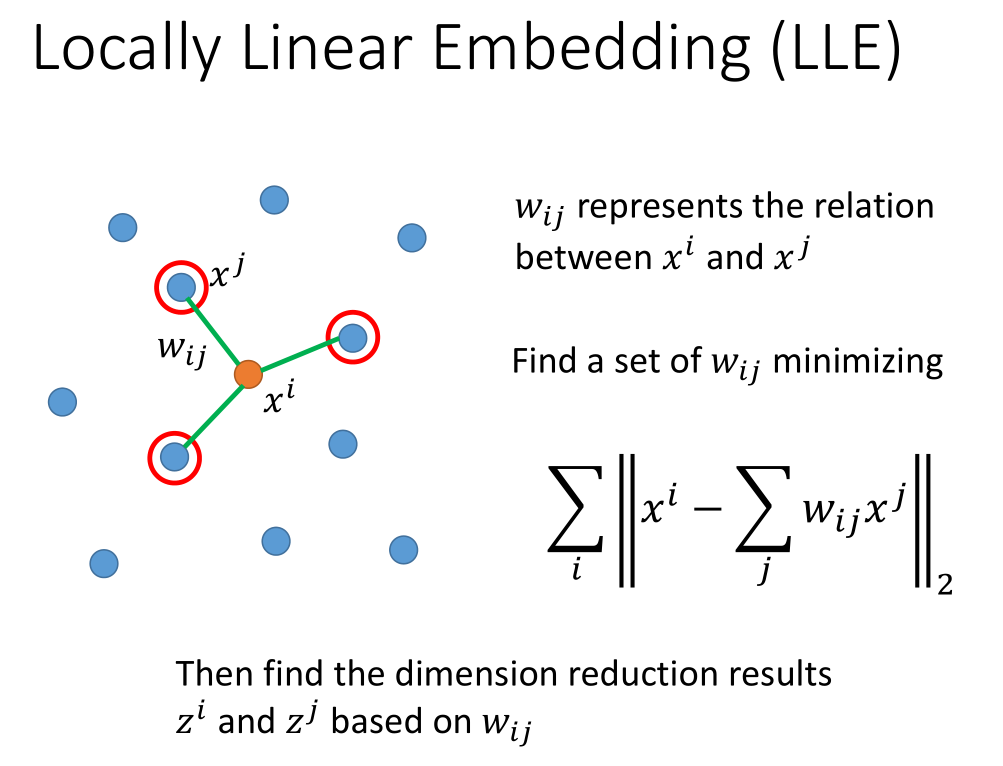
从原来的分布中找一点$x^i$,然后找它的 neighbour $x^j$,计算它们之间的关系$w_{ij}$。
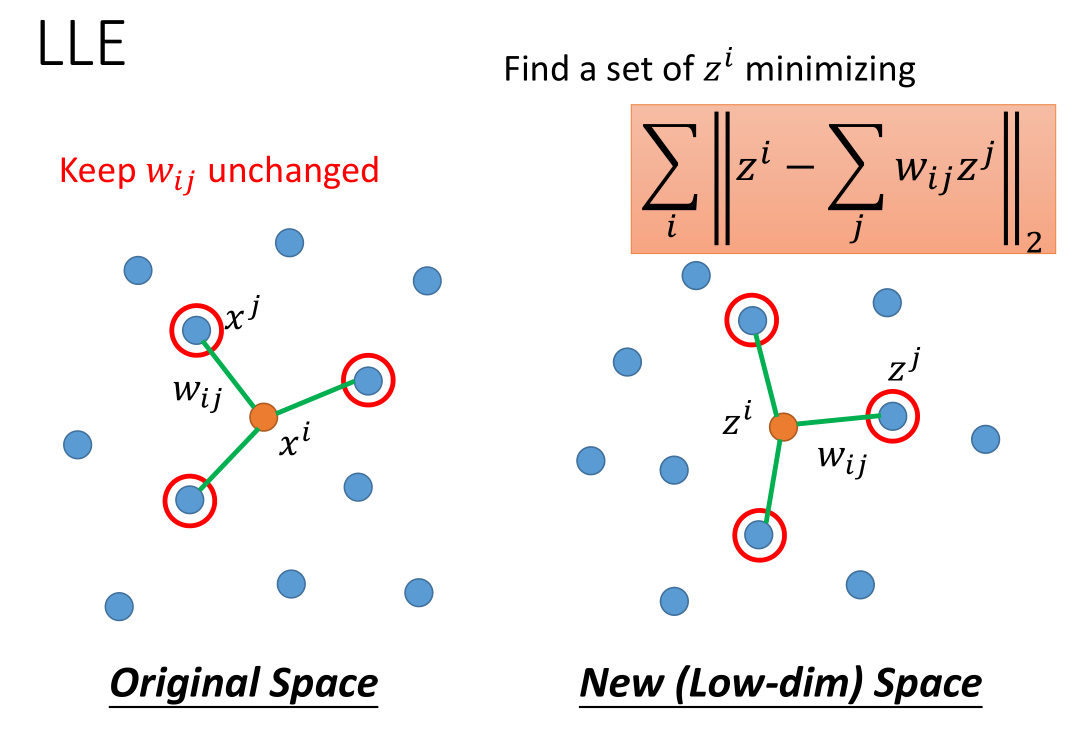
把$x^i$,$x^j$ 降维成$z^i$,$z^j$ 之后要保证它们之间的$w_{ij}$ 不变。
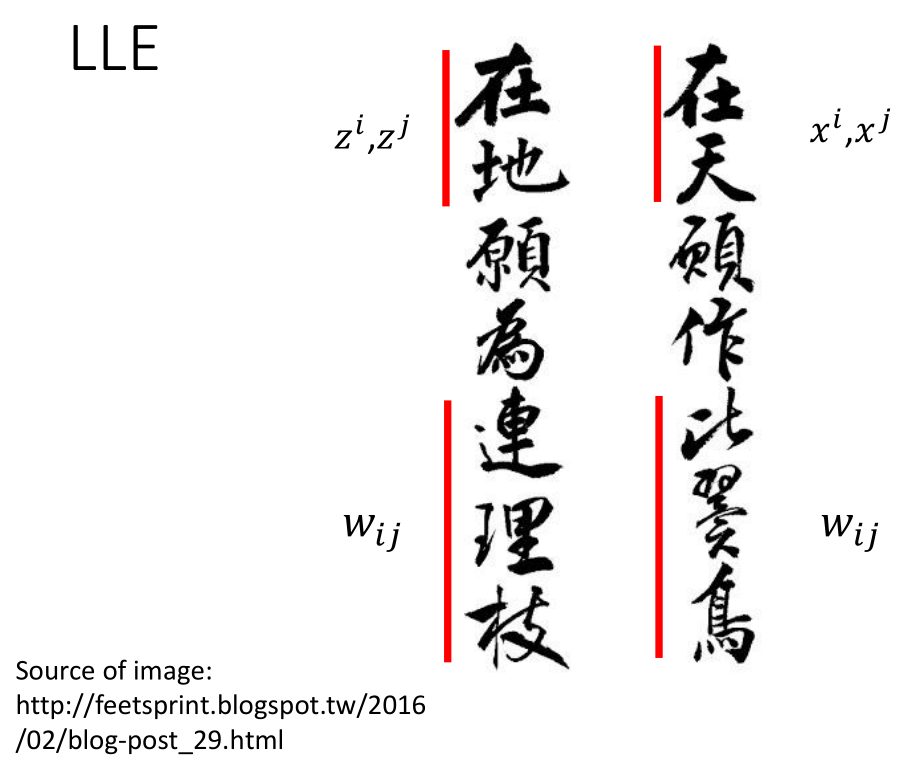
“在天”等价于在原来的数据集$x^i,x^j$,他们之间的关系:”比翼鸟”等价于$w_{ij}$
transform 后:
“在地”等价于在原来的数据集$z^i,z^j$,他们之间的关系依然是:”连理枝”等价于$w_{ij}$
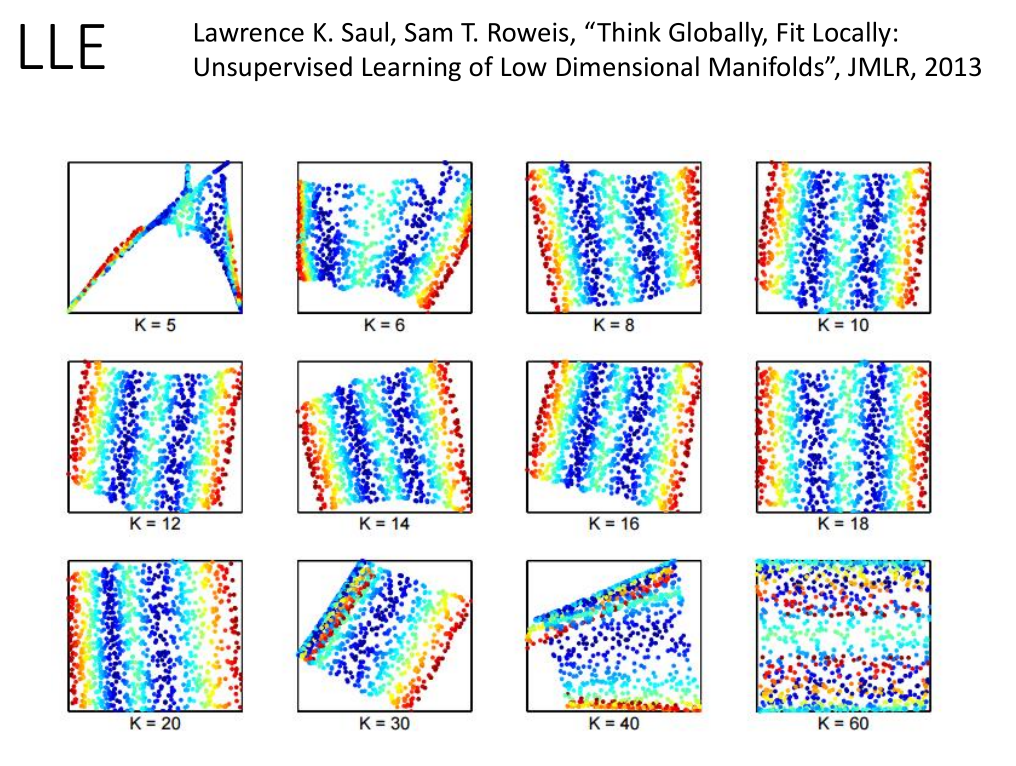
LLE没有明确的 function 做降维。
LLE的好处是,就算不知道xi,xj 只知道wijwij ,也可以用 LLE 。
要好好调 neighbour 的个数,刚刚好才会得到好的结果。
点之间的距离关系保持不变需要点之间够近,所以 k 不能太大。
3. 拉普拉斯特征映射
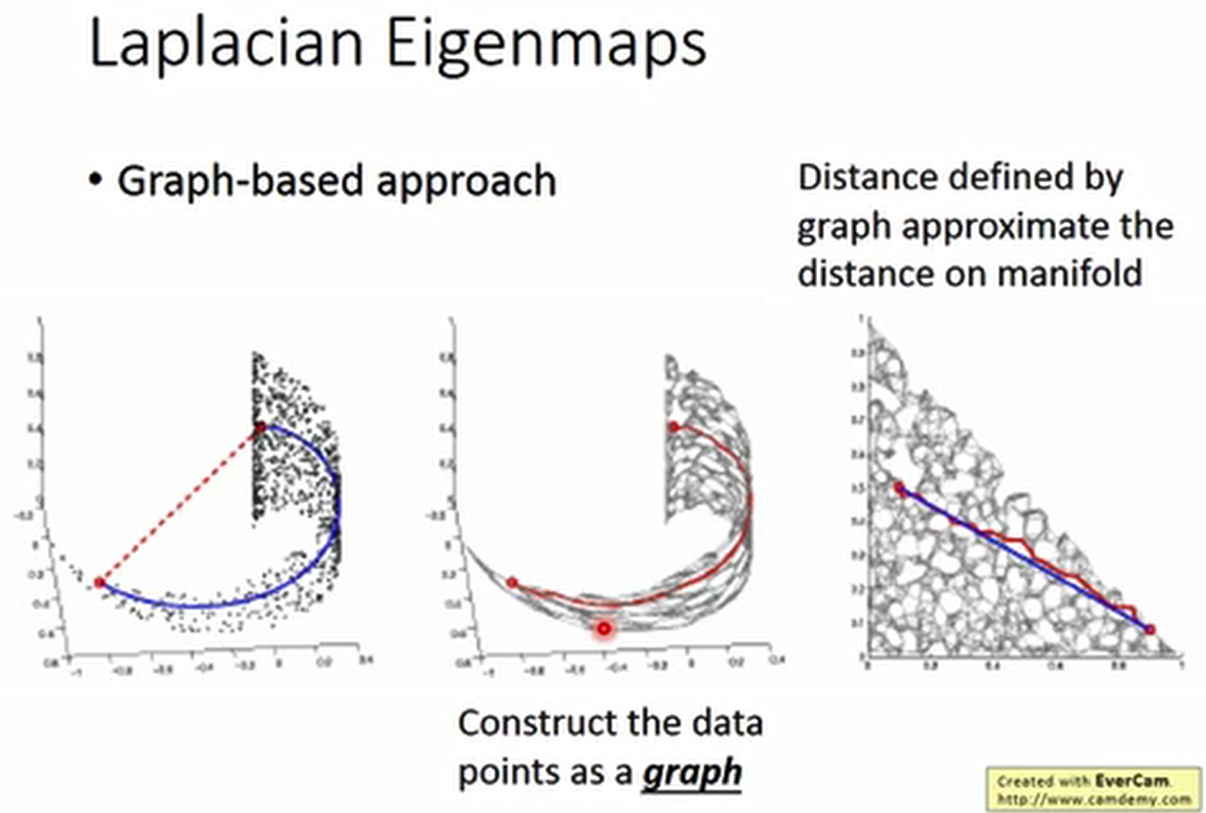
两个红点之间的距离不能用欧氏距离还衡量,
要看两点之间有没有高密度区域的链接,可以建立一个图,用图中的距离来表示。
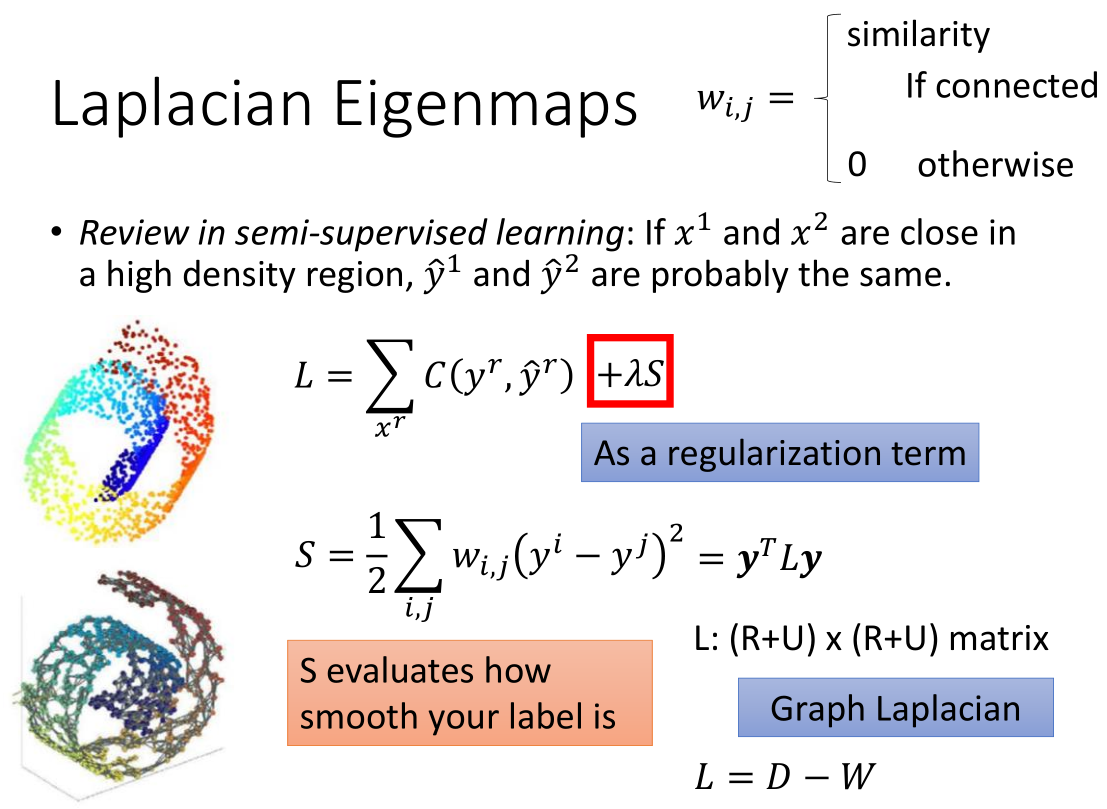
回顾半监督学习:红框里那项与 labelled data 无关,
它利用 unlabelled data 考虑得到的 label 是否 smooth,作用类似于正则项。

计算 S 时对 z 要加一个约束:
设 z 是 M 维的,则 $z^1,z^2,…,z^N$ 张成 $R^M$ 空间。
这样解出 z 。z 就是 graph laplacion L 的特征向量,对应比较小的特征值。
4. T-distributed Stochastic Neighbor Embedding (t-SNE)
T 分布随机近邻嵌入算法(t-SNE)
前面方法只假设相近的点接近,但未假设不相近的点要分开。

把相同的数字放在一起,但是没办法把不同的数字分开。
故有可能把不相似的物体也放在一起。故挤成一团,如上图所示。
- t-SNE 计算过程

t-SNE 先分别计算原空间、新空间中所有点对的相似度再归一化。
归一化是必要的,为了防止两个空间中距离的 scale 不同。
然后最小化二者之间的 K-L 距离,代入公式用 GD 即可。
t-SNE 计算量大,可先用 PCA 降维,再用 t-SNE 降维。
t-SNE 需要一堆 data point ,然后找到z。
如果之后再给一个数据,t-SNE 是没法做的,只能再跑一遍。
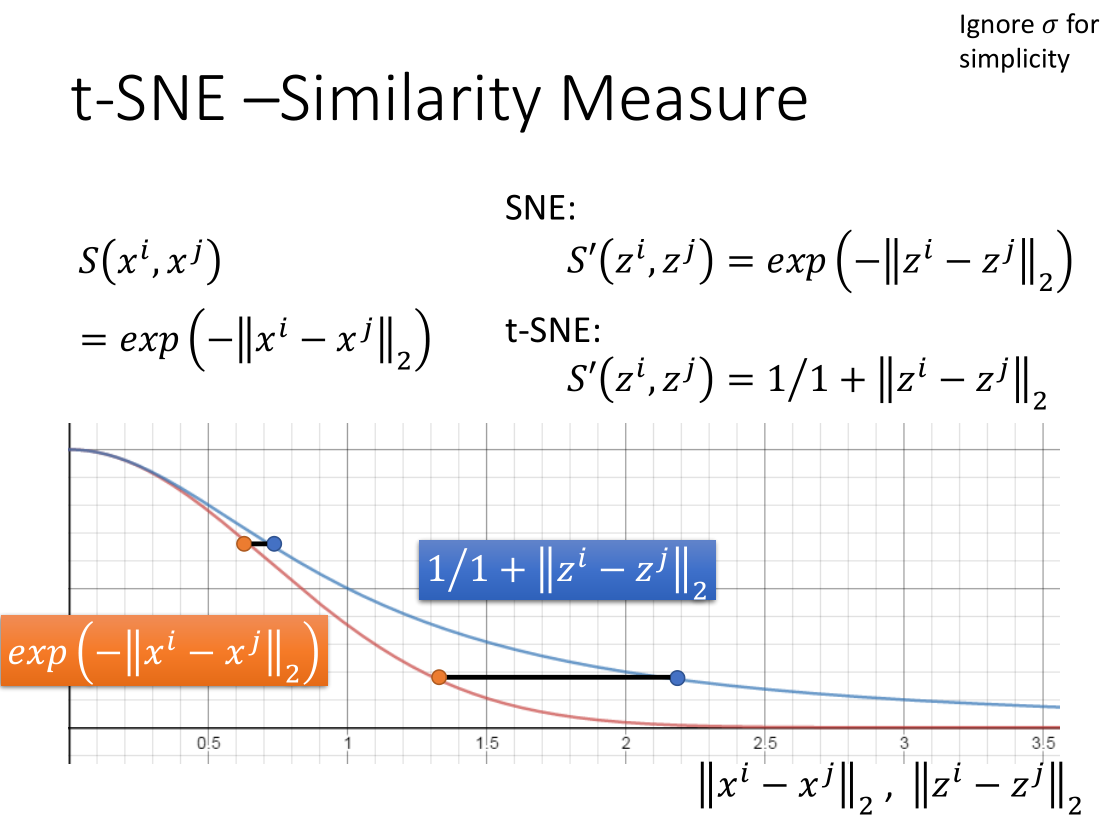
t-SNE 的神妙之处在于原空间与新空间中相似度计算公式不同。
原空间的计算公式,使得两个点的相似度随距离增加快速下降。
而新空间的计算公式,是长尾的,为了维持相同的相似度,两个点之间要分得更开。
对原来距离很近的点,影响很小。而原来离得远的点,会被拉开。
效果如图:
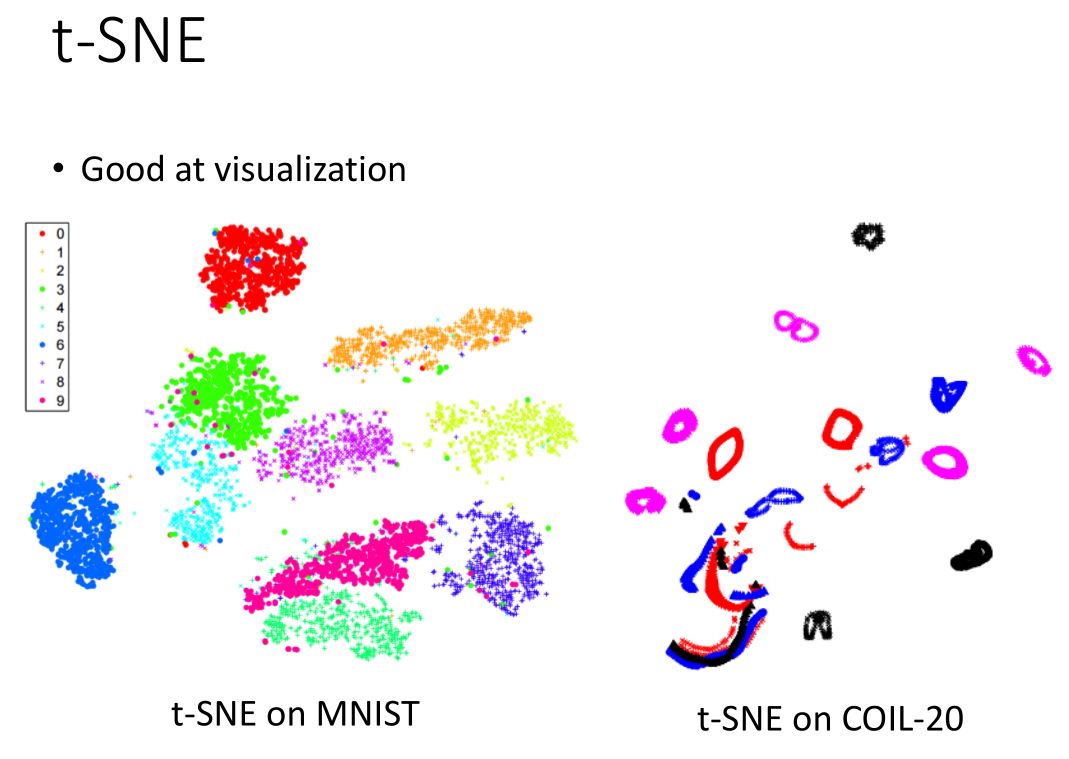
t-SNE参考资料:
- https://github.com/oreillymedia/t-SNE-tutorial
- Laurens van der Maaten, Geoffrey Hinton,“Visualizing Data using t-SNE”, JMLR, 2008
5. 总结
- 流形学习
- 局部线性嵌入
- 拉普拉斯特征映射
- T-distributed Stochastic Neighbor Embedding (t-SNE)