这一节我们主要学习
- 梯度下降法
- 梯度下降法小技巧,比如 Adagrad、随机梯度下降法、特征放缩等。
1. 梯度下降法 (Gradient Descent)

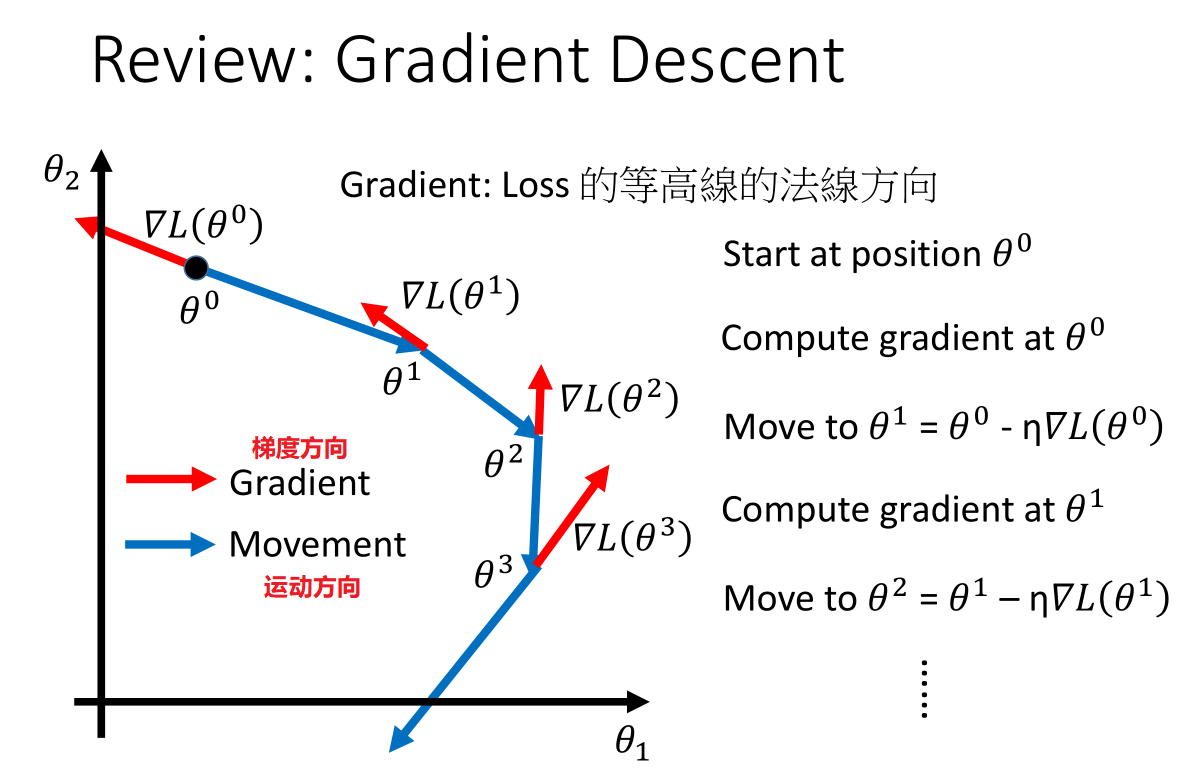
上图中:红色是梯度方向,蓝色是梯度下降方向,横纵坐标都是参数,故可以看作是损失函数的等高线。
而梯度方向是损失函数等高线的法线方向。
2. 调整学习率 (Learning Rate)
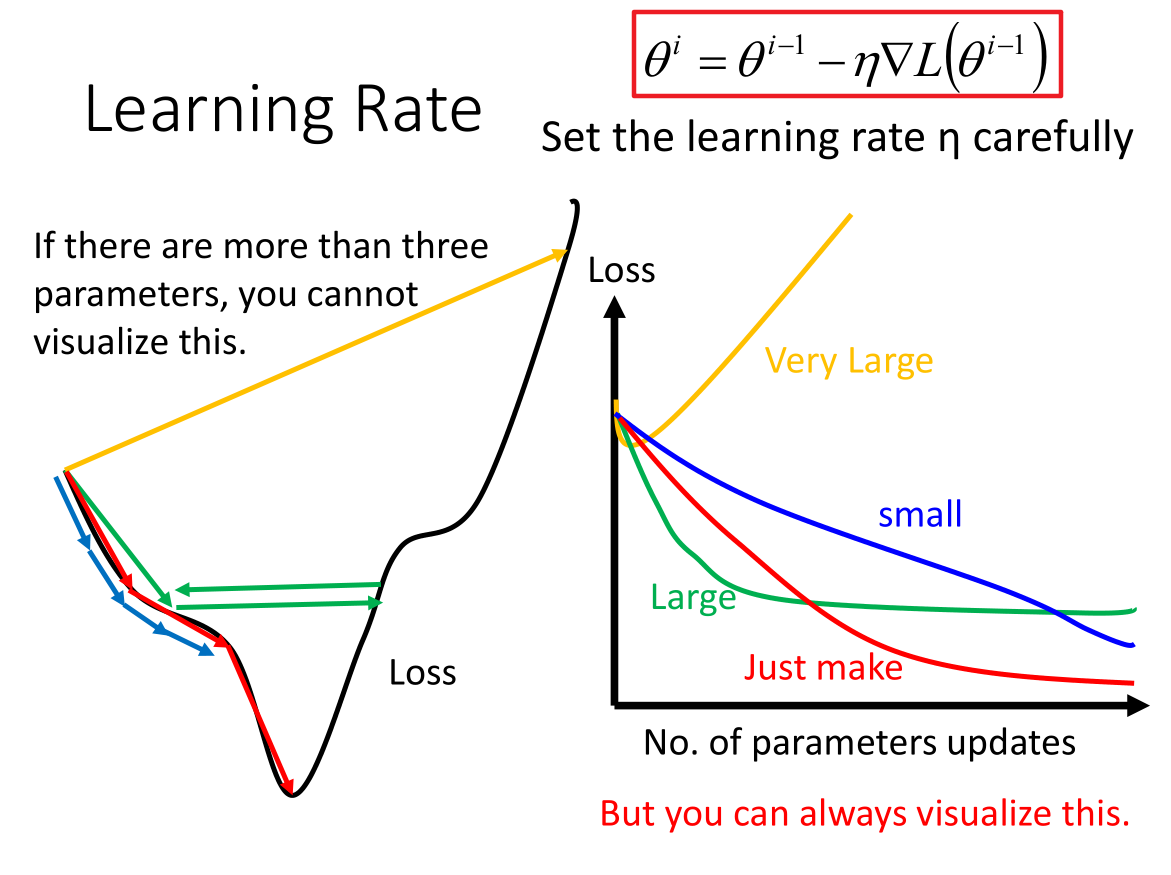
上图主要理解学习率对损失函数的影响。
左边的横坐标是学习率、右边的横坐标是参数的迭代次数。
- 各种颜色代表含义:
- 蓝色:学习率过小的情况
- 红色:学习率刚刚好
- 绿色:学习率偏大情况
- 黄色:学习率过大情况 </br>
-
蓝色:学习率过小,找到最优解需要迭代的次数比较多,损失函数变化比较缓慢。
-
红色:学习率刚刚好,找到最优解迭代的步数刚刚好,损失函数变化也刚刚好。
-
绿色:学习率过大,在找最优解时可能跳过或者如上图所示,在那附近循环,损失函数下降很快并不再变化。
- 黄色:学习率太大,损失函数可能不降反真。
只有把学习率调整的刚刚好,才能得到最适合曲线。
3. 使用Adagrad来自动调整学习率 (Adaptive Learning Rate)
学习率简单常见的基本原则:学习率通常随着参数的更新会越来越小。
-
在起始点,距离目标比较远,需要大一点的学习率;
-
迭代多次以后,比较靠近目标,此时需要小一点的学习率,使其收敛于最低点
-
假设第t次学习率设置为:$\eta^t = \eta/\sqrt{t+1}$
-
每个不同的参数有自己不同的学习率
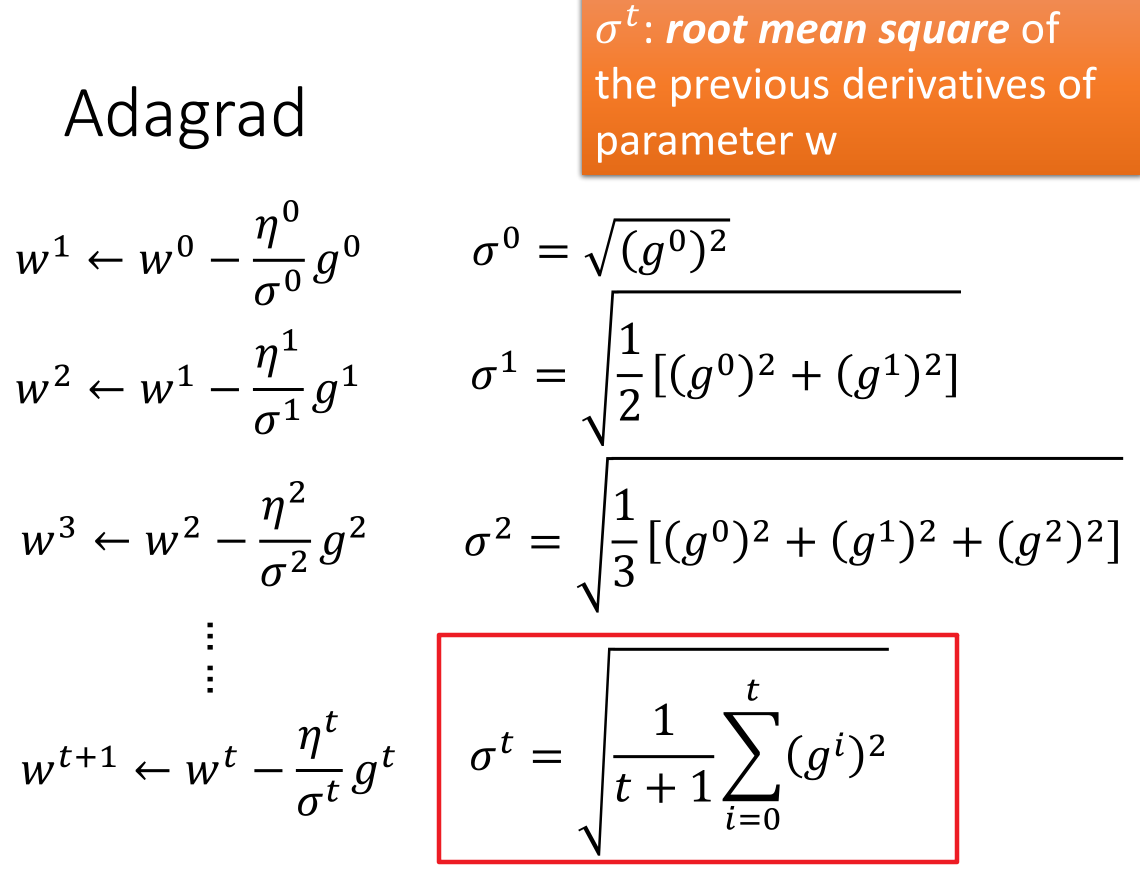
3.1 Adagrad 定义和表达式
Adagrad 自适应地为各个参数分配不同学习率的算法

注意:上式中 $g^t = \frac{\partial L(\theta^t)}{\partial{\theta}}$
- 理解 $\sigma^t$ 和推导公式过程
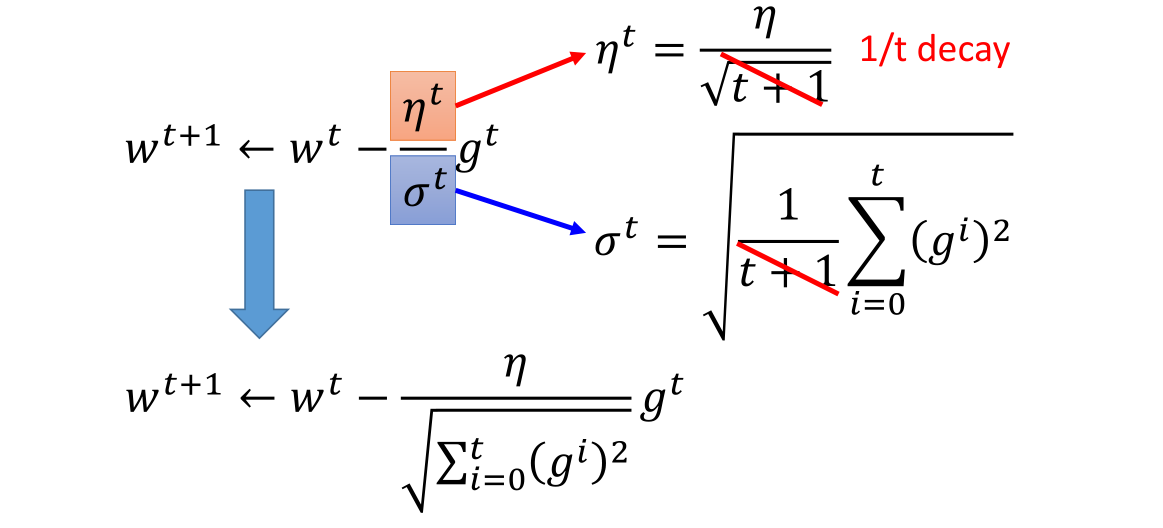
3.2 理解 Adagrad 反差问题
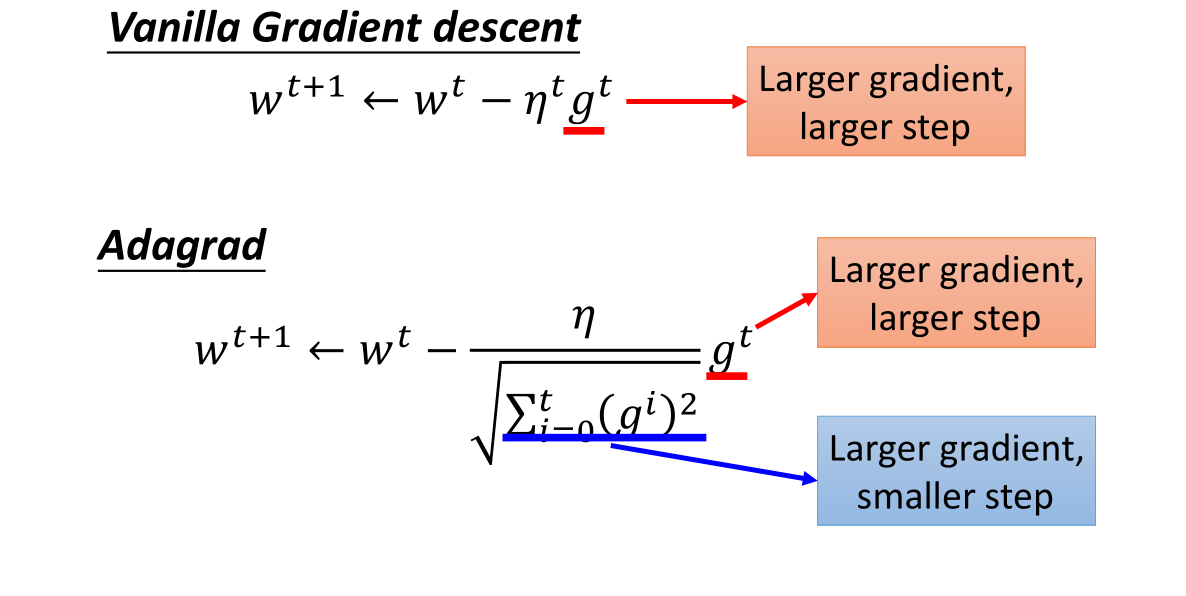
$g^t$ 越大,每次迭代的步幅就越大;
$\sqrt{\sum_{i=0}^t (g^i)^2}$ 越大,每次迭代的步伐就越小;
即:分子部分参数偏微分越大,更新步伐就越大;而分母越大,则每次更新的步伐就越小。
那么如何理解这一部分呢?
- 直观解释

- 具体解释
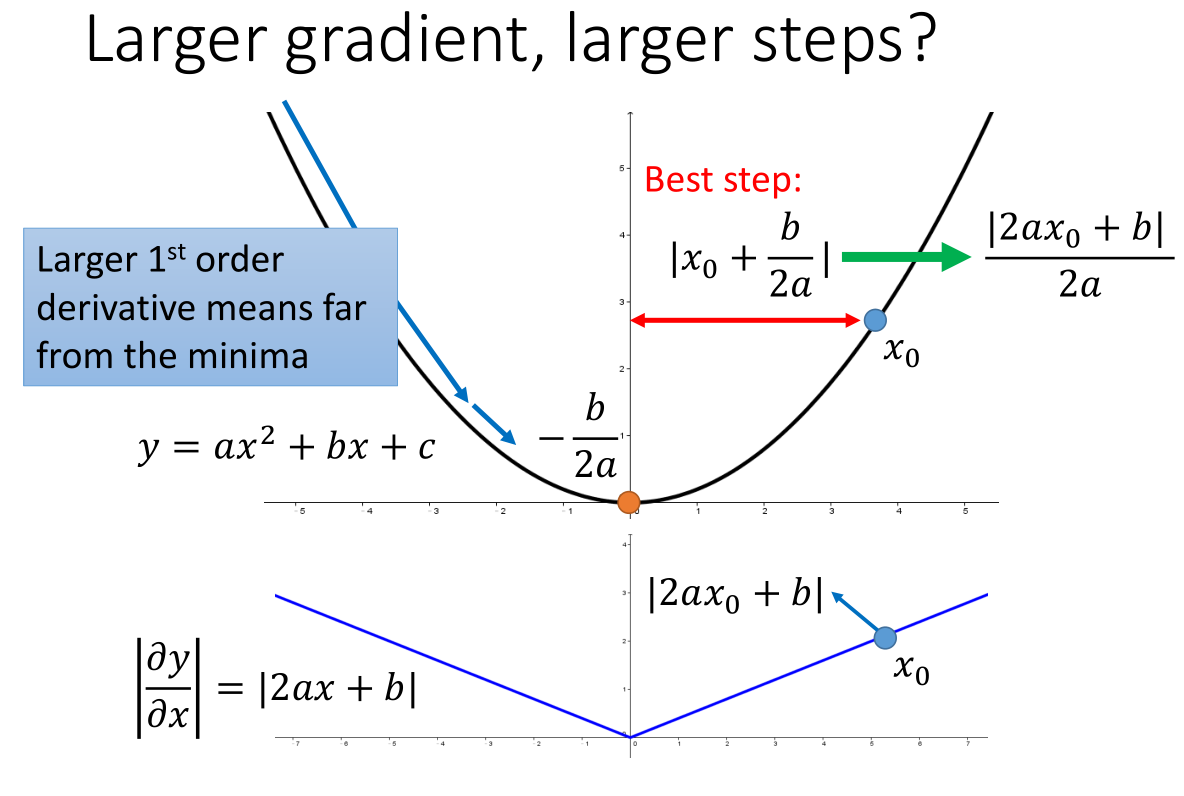
假设上图中 $x_0$ 是初始点,求二次函数的最低点:
最好的步伐就是该点到对称轴的距离 $|x_0-(-\frac{b}{2a})|=\frac{|2ax_0+b|}{2a}$
而二次函数的倒数绝对值就是 $|2ax_0+b|$
因此:最好的步伐是与微分的大小成正比(针对一个参数时成立)
- 考虑多个参数微分与步伐的关系
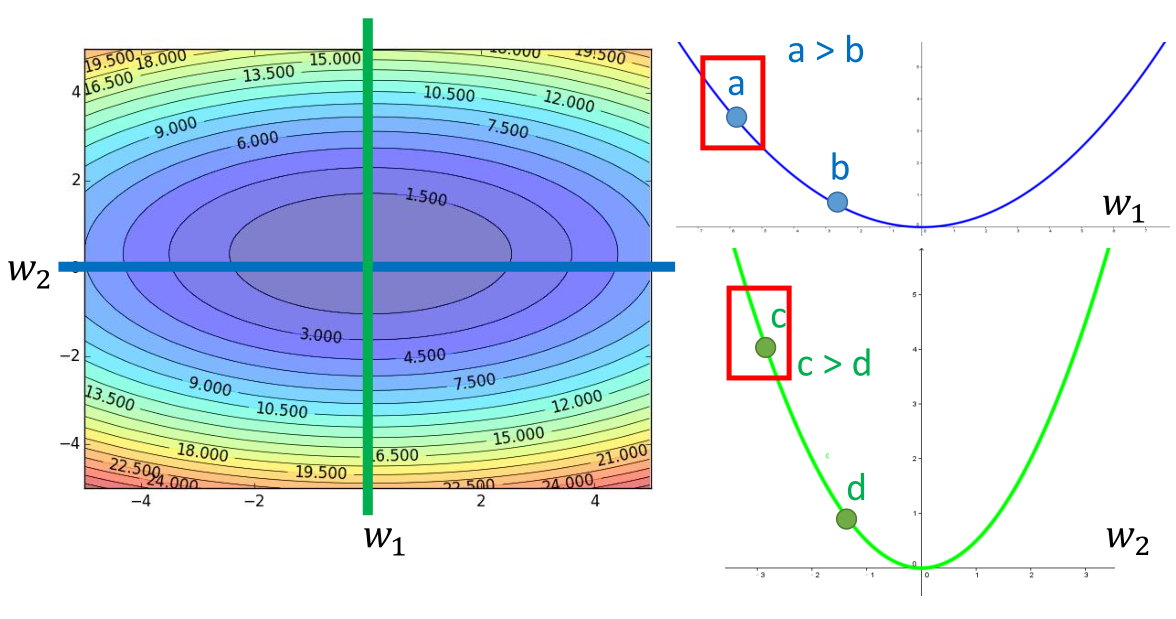
此时考虑 2 个参数微分与步伐之间的关系:
如果仅考虑 a 与 b 或者 c 与 d 之间微分与步伐的关系,答案是很明显的。
距离最低点越远的微分值比较大。
考虑 a 对 w1 的微分和 c 对 w2 的微分,上面的答案就不正确。
此时我们发现:
二次函数初始值 $x_0$ 到最低点的距离表达式 $\frac{| 2ax_0 +b | }{2a}$ 的分母项 2a
正好是二次函数对 x 的二次微分。
故最好的步伐是:$|First derivative| \/ Second derivative$
即 $\frac{|f’(x)|}{f’‘(x)}$
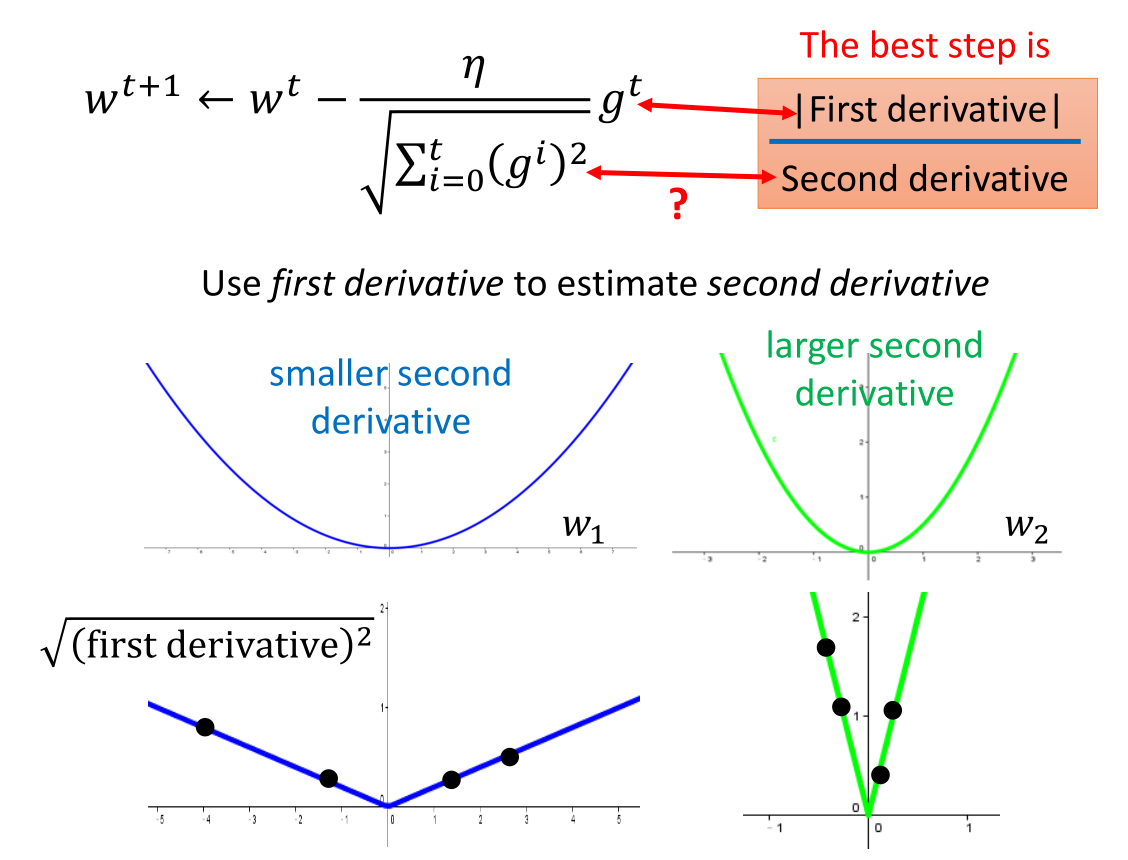
$\sqrt{\sum_{i=0}^{t}(g^i)^2}$ 反应了二次微分的大小
4. 随机梯度下降法 (Stochastic Gradient Descent)

梯度下降法的一般流程是:
-
计算全部训练集的损失函数 L
-
计算相关参数梯度并更新参数权重
随机梯度下降法的流程是:
-
选择训练集中的一个样本 $x^n$ ,可以随机取也可以按照顺序取
-
损失函数也只是一个样本的损失函数 $L^n$
-
计算参数梯度也只是计算一个样本对应的参数梯度并以此更新参数权重
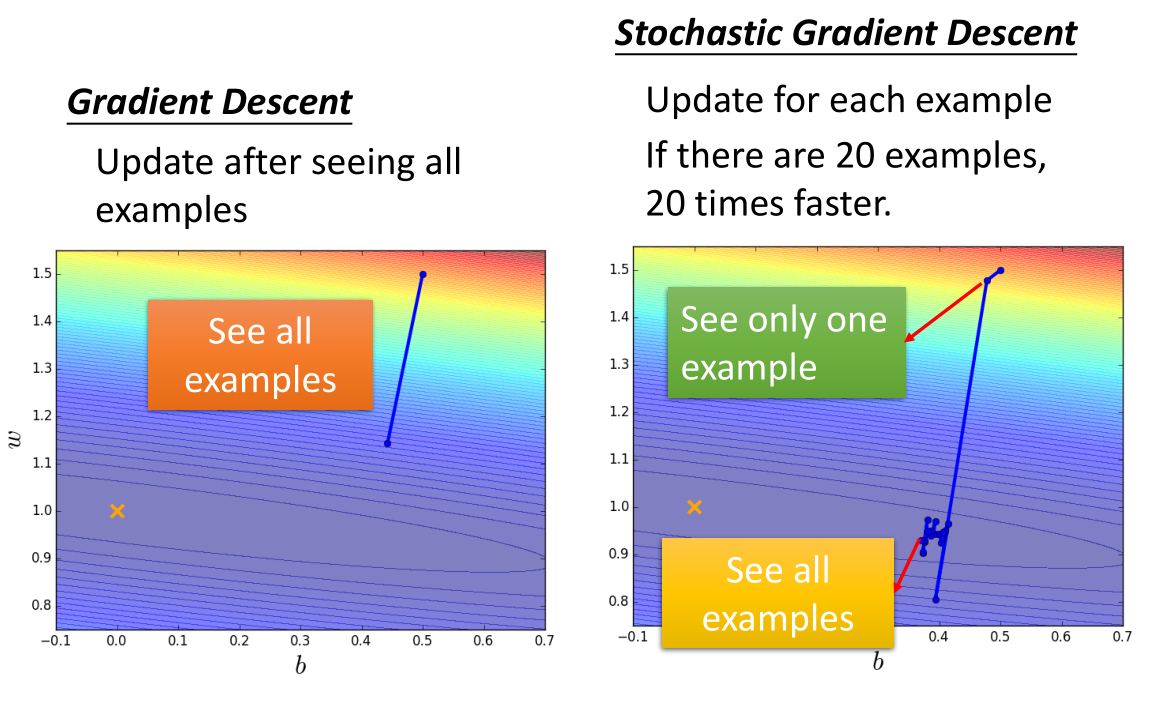
梯度下降法参数更新过程如上图左边,参数更新方向就是极值点方向。
随机梯度下降法参数更新过程如上图右边,每个样本参数更新一次,如果有 20 个样本就更新 20 次。
5. 特征缩放(Feature Scaling)
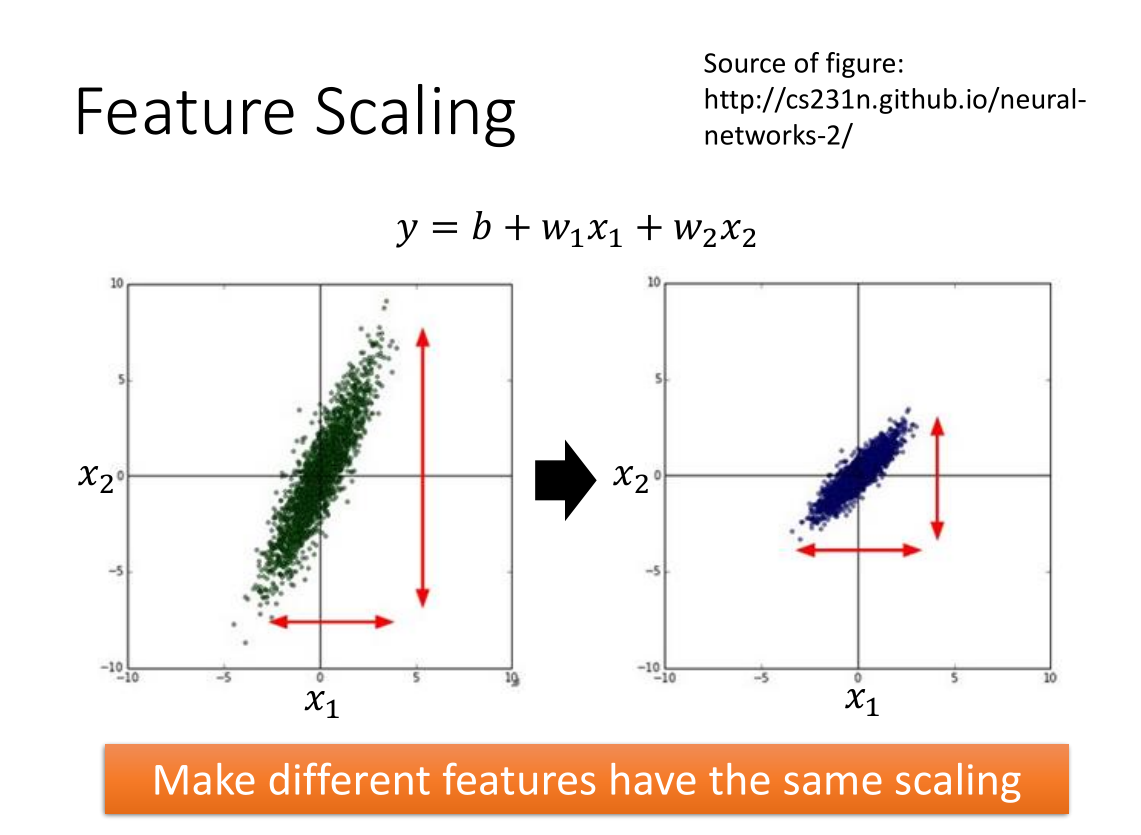
上图中 x1 与 x2 分布不一致且 x2 分布远比 x1 大,把 x2 特征缩放后如图右边所示,二者特征分布一致。
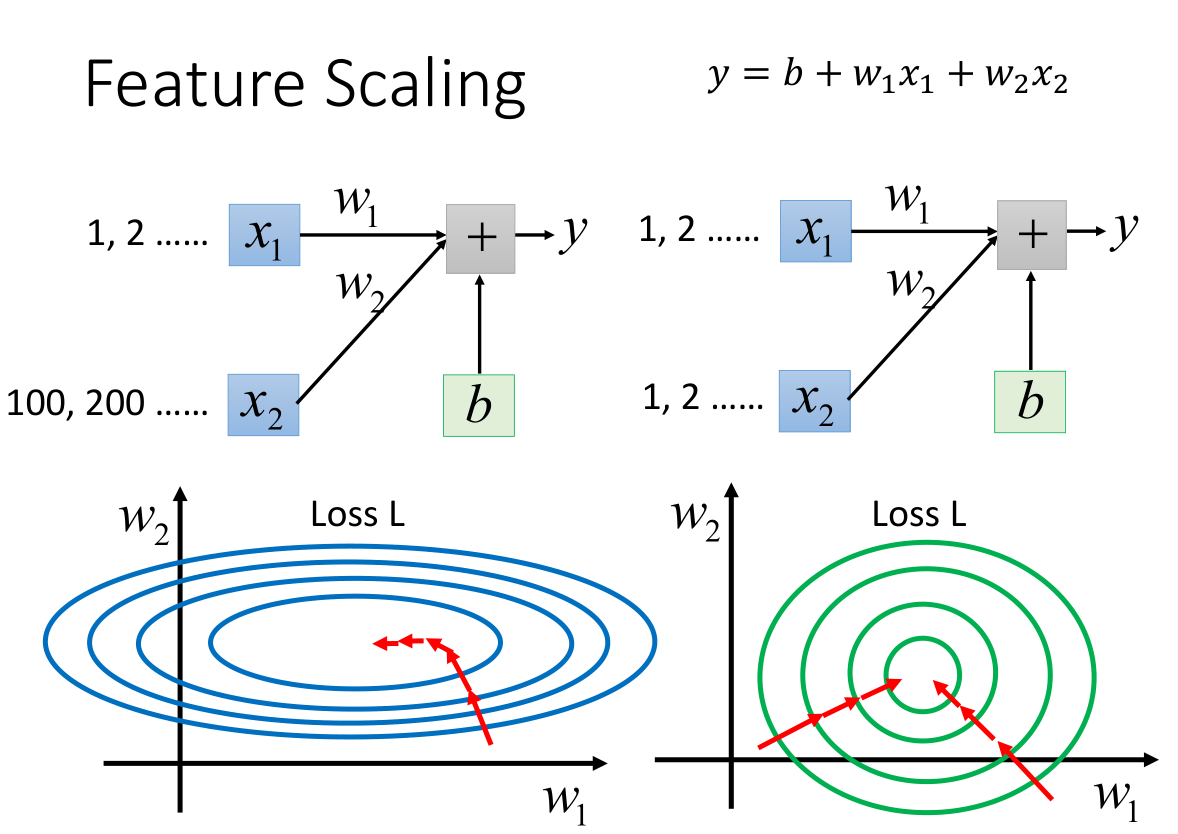
- 特征缩放的作用:
上图表示特征缩放前后参数对损失函数的影响;
没有特征缩放的参数很难找到损失函数极值点(椭圆中心和圆中心)。
特征缩放后分布一致,更新参数也很容易,找到损失函数的极值点也容易。
可以理解是每次参数更新的方向是损失函数等高线的法线方向,很明显椭圆等高线的法线方向实时变化,而圆的法线方向一直指向圆心。
- 特征缩放常见的方法:
特征标准化(特征均值是0,方差是1)
$x_i = \frac{x_i-\mu}{\sigma}$
6. 梯度下降法理论 (Theory)
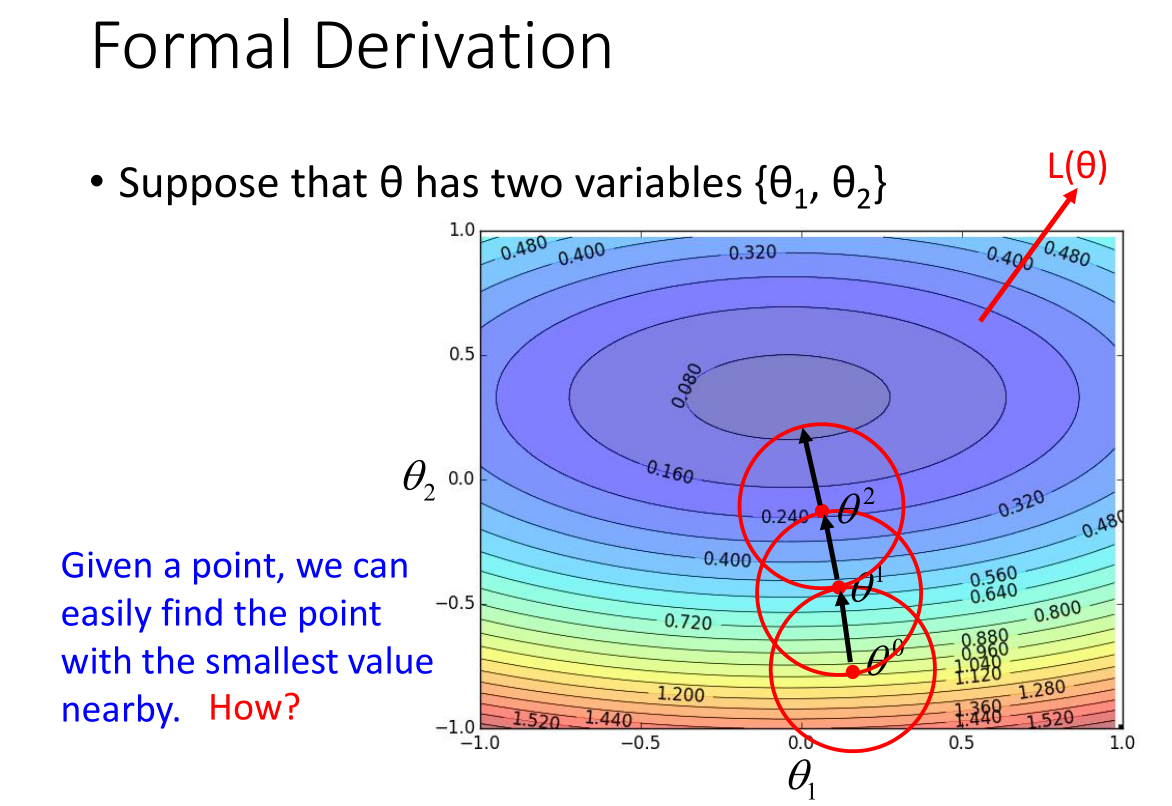
假设参数 $\theta$ 有两个变量 {$\theta_1,\theta_2$},参数与损失函数关系如上图。
然后在起始点 $\theta^0$ 为圆心,绘制一个圆,找到圆上最小值点 $\theta^1$;
之后在起始点 $\theta^1$ 为圆心,绘制一个圆,找到圆上最小值点 $\theta^2$;
依次内推,一直找到最小值点附近。
问题:怎么很快的在红色圆圈里面找到让损失函数最小的参数?
- 泰勒公式

- 多元泰勒展开

按照泰勒公式对函数进行展开。
- 梯度下降与泰勒公式相结合
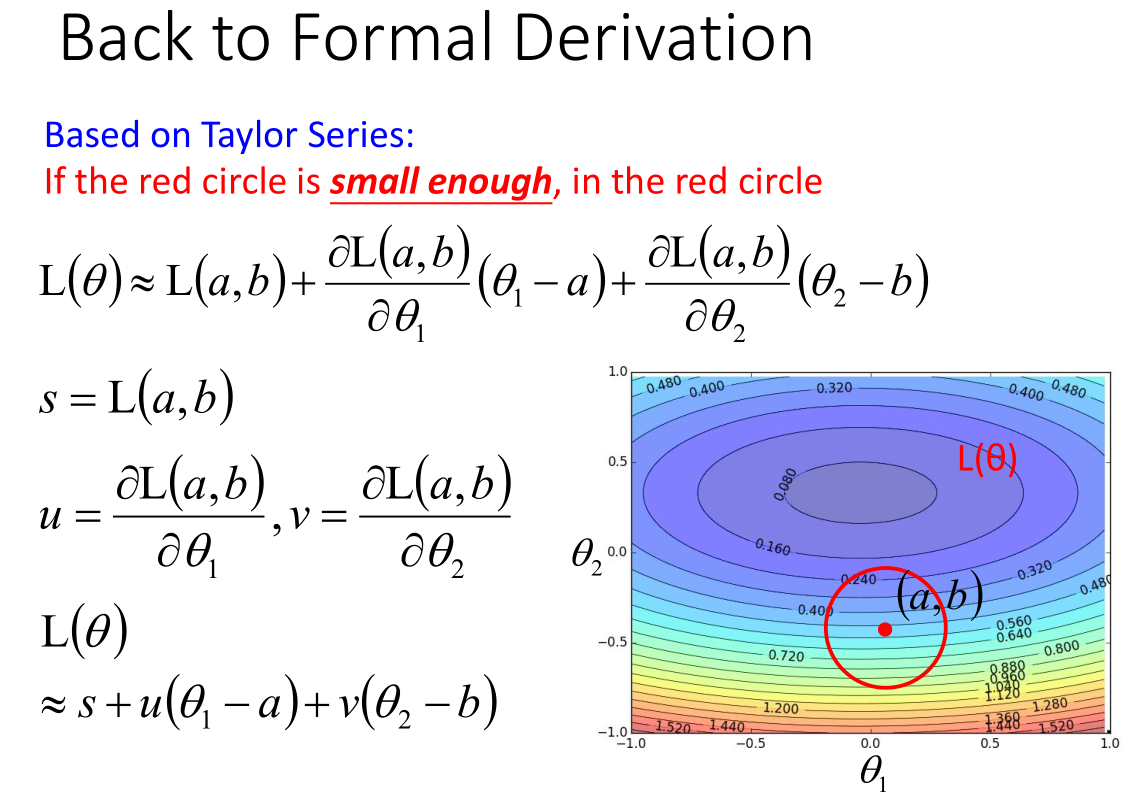
假设红色圆圈足够小,红色圆圈圆心 (a,b),在红色圆圈内,用泰勒公式对损失函数进行简化:
$L(\theta)\approx L(a,b)+\frac{\partial L(a,b)}{\partial \theta_1}(\theta_1-a)+\frac{\partial L(a,b)}{\partial \theta_2}(\theta_2-b)$
将常数项简化:
$s = L(a,b)$
$u = \frac{\partial L(a,b)}{\partial \theta_1}$
$v = \frac{\partial L(a,b)}{\partial \theta_1}$
即关键表达式:
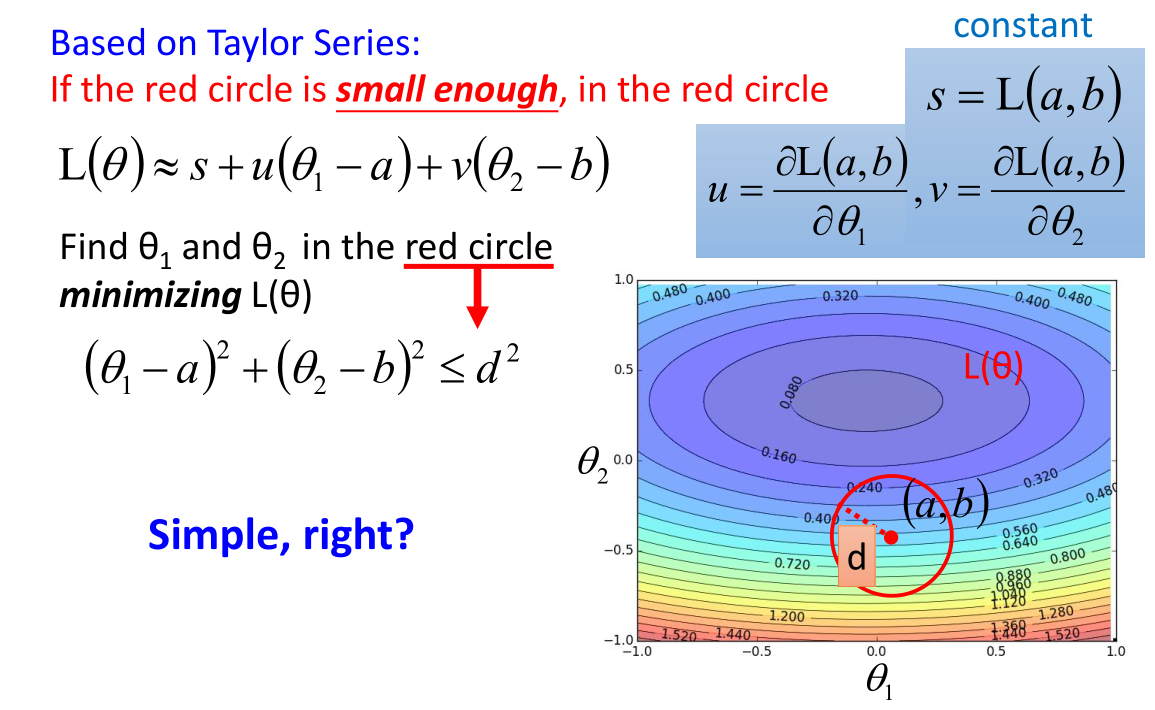
$L(\theta) \approx s + u(\theta_1-a)+v(\theta_2-b)$
红色圆圈范围内表达式:
$(\theta_1-a)^2+(\theta_2-b)^2 \leq d^2$
上述问题转化为:
满足红色圆圈范围内的 {$\theta_1,\theta_2$},使得损失函数 $L(\theta) \approx s + u(\theta_1-a)+v(\theta_2-b)$ 最小。
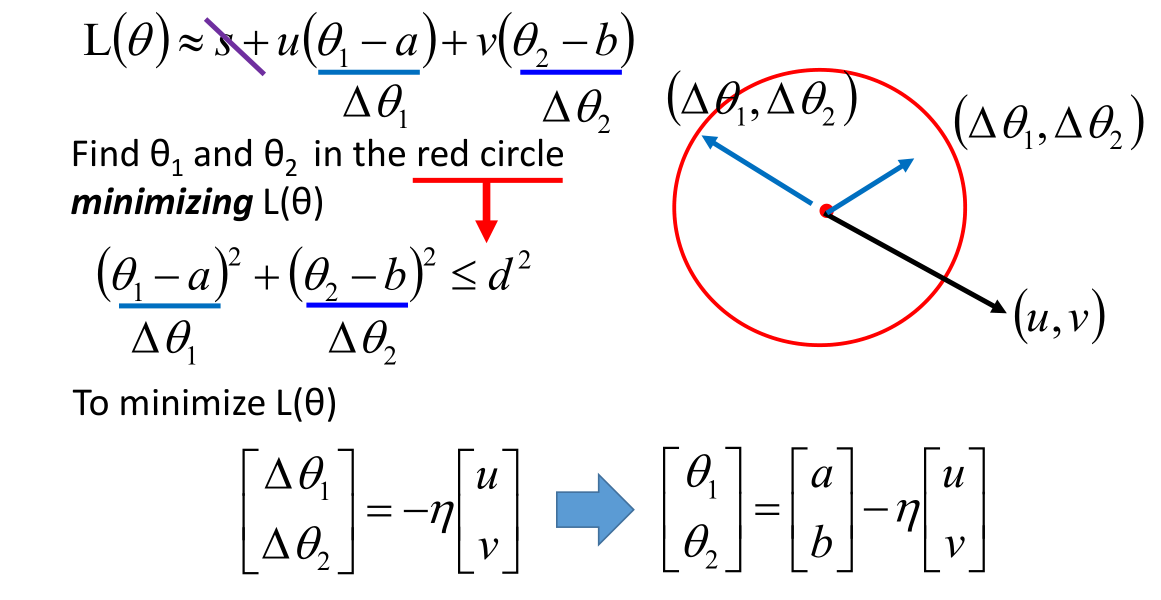
按照梯度下降法进行求解,得到参数 $\theta_1,\theta_2$ 近似解的表达式。
7. 梯度下降法的限制 (More Limitation of Gradient Descent)
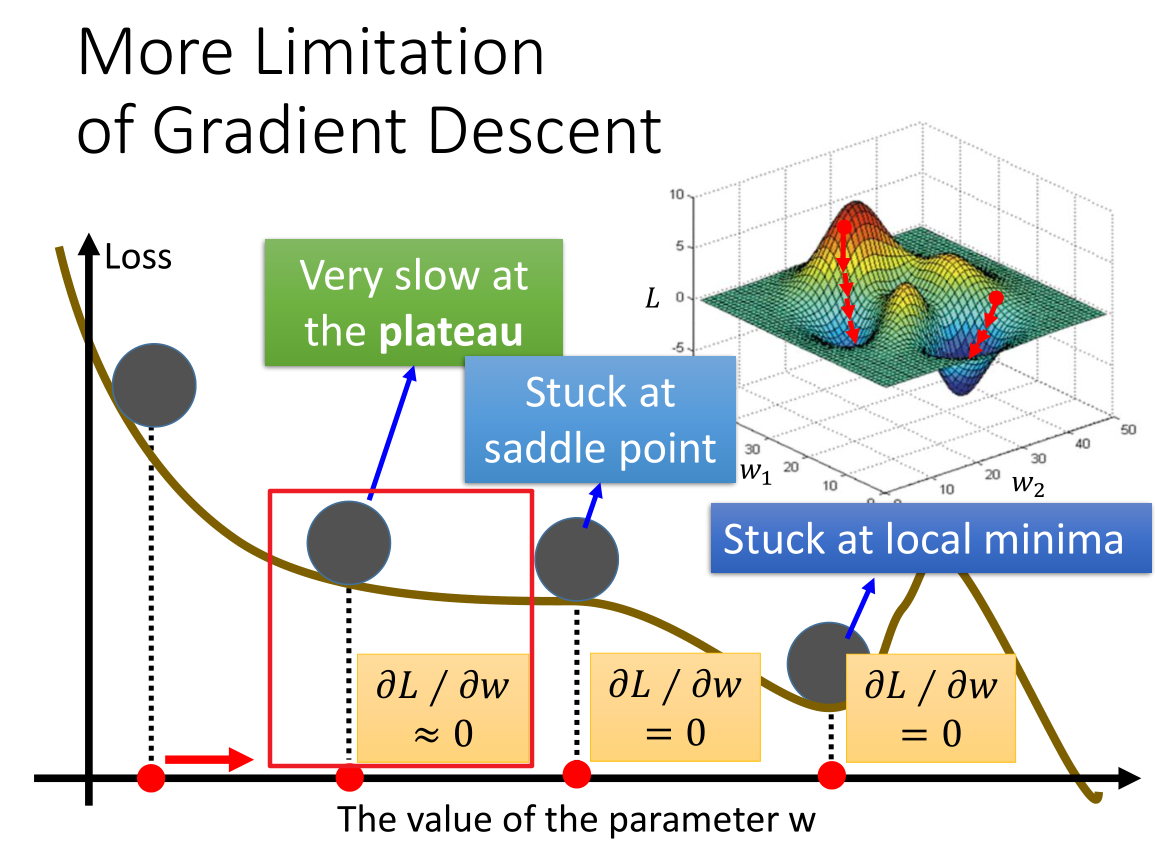
梯度下降过程中,局部最优解和鞍点不是最主要的。
最严重的是图中红色方框的位置,我们计算其微分值小于一个非常小的数($10^{-6}$)是时就认为其微分值为 0,而实际上此时不一定比较接近最优解。