这一节我们主要学习
- 无监督学习的分类
- 聚类
- 分布式表征(Distributed Representation)
- 降维(Dimension Reduction)
- PCA 主成分分析
- 矩阵分解
1. 无监督学习的分类
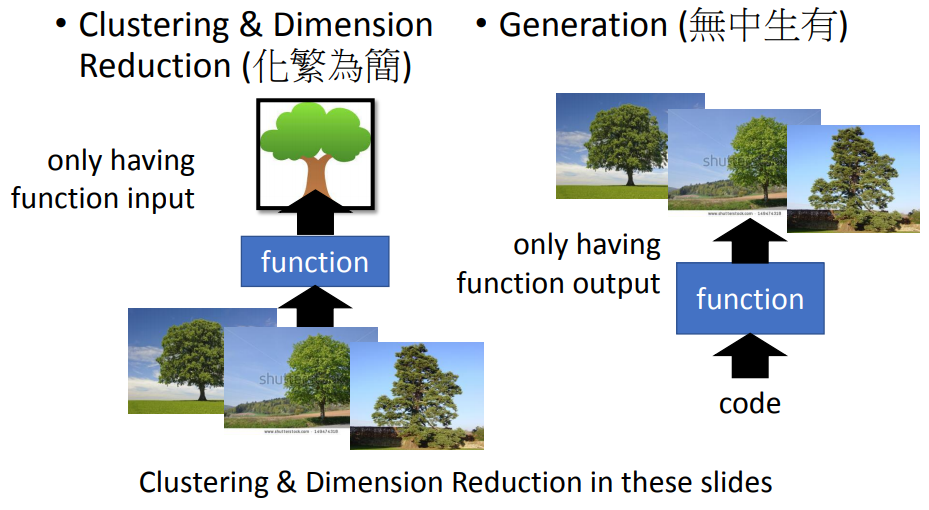
- 聚类和降维(化繁为简)
复杂的input —> 简单的output,训练时只有一堆输入,不知道输出 - Generation(生成器,无中生有)
随机输入(比如输入不同的数字)得到不同的输出(image)
知道输出(image),但是不知道输入
2. 聚类

关键问题:聚类的个数
2.1 k-均值聚类(K-means)
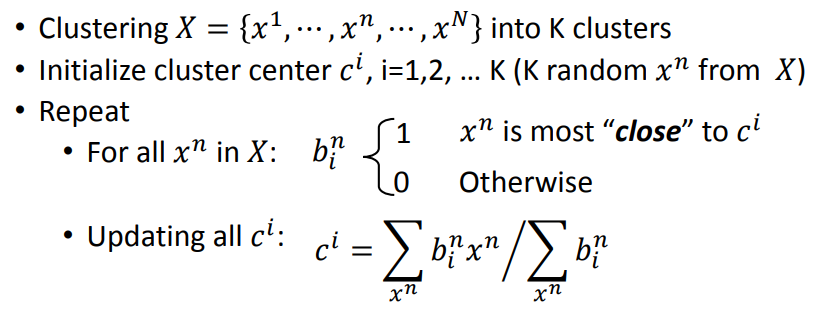 + 将样本 X={x1,x2…xN} 聚合成 K 个类
+ 将样本 X={x1,x2…xN} 聚合成 K 个类
- 初始化类中心 ci,i=1,2,…K
- 重复
- 利用 ci 将样本分为 K 各类
- 利用分好的 K 个类中的样本重新算出每一个类的 ci
2.2 分级聚类(Hierarchical Agglomerative Clustering(HAC))
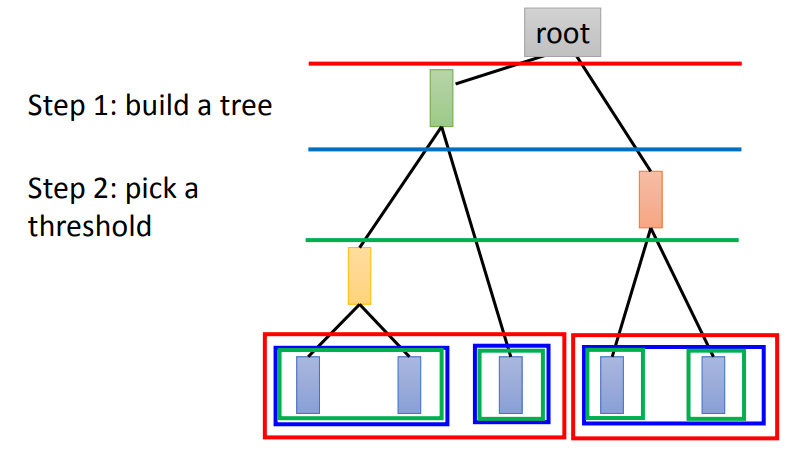 假设有5个样本,计算两两之间的相似度,将最相似的两个样本聚合在一起(比如第一个和第二个)
假设有5个样本,计算两两之间的相似度,将最相似的两个样本聚合在一起(比如第一个和第二个)
再将剩下的4个聚合在一起,以此类推。
3. 分布式表征(Distributed Representation)
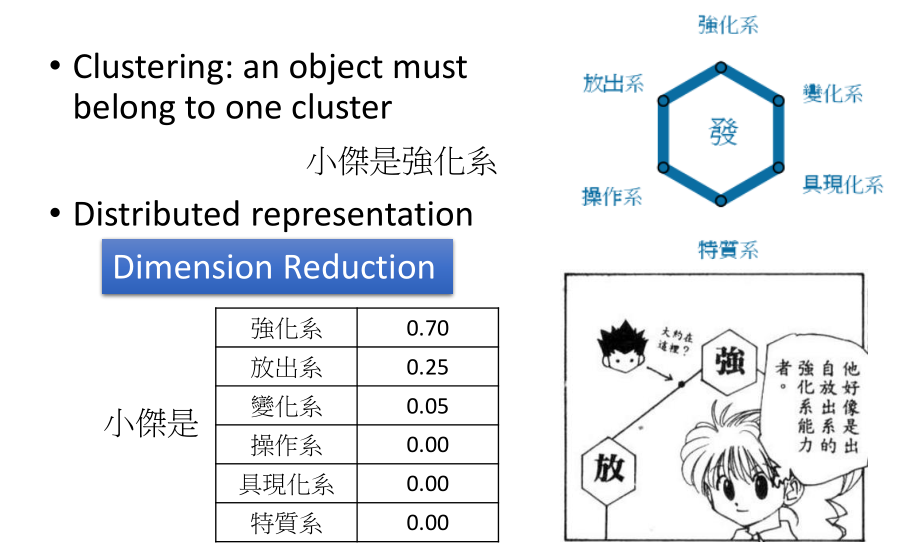 仅仅做聚类是不准确的,有的个体并不只属于一个大类,所以需要一个向量来表示在各个类中的概率。
仅仅做聚类是不准确的,有的个体并不只属于一个大类,所以需要一个向量来表示在各个类中的概率。
这样,从一个(高维)图片到一个各属性概率(低维)就是一个降维。
- 聚类:一个对象必须属于一个类别;
- 降维:直接按照特征的分布来选取有分布的特征。
4. 降维(Dimension Reduction)
为什么说降维是很有用的呢?
有时候在3D种很复杂的图像到2D种就被简化了

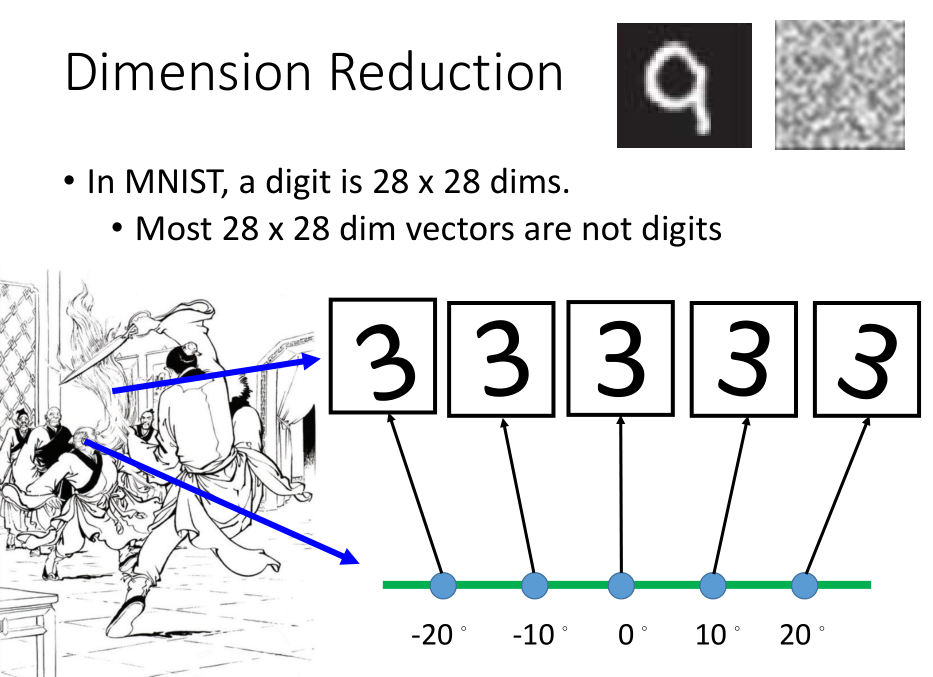
在 MNIST 训练集中,很多28X28维的向量转成图像看起来根本不像数字,
直觉上可以理解向量中与数字有关的向量维数较少(背景的像素点均为无效向量),所以我们可以用少于28X28维的向量来描述它。
比如上图一堆3,每一个都是28X28维的向量,但是我们发现,它们仅仅是角度的不同,
所以我们可以加上角度值进行降维,来简化表示。
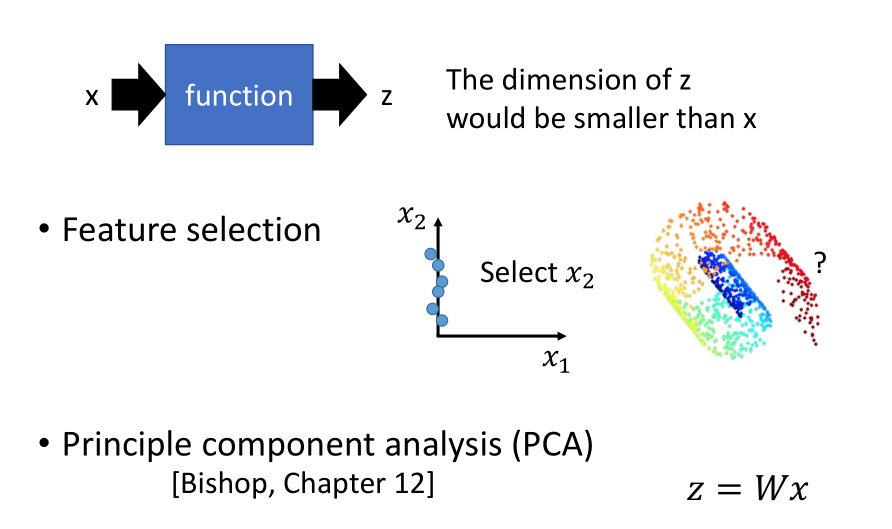
降维一般有两个方法:
- 特征选择(Feature selection ):
比如在左图二维坐标系中,我们发现X1轴对样本点影响不大,那么就可以把它拿掉。
- 主成分分析(PCA ):
输出 z=Wx 输入,找到这个向量 W 。
5. 主成分分析(PCA)
5.1 PCA原理
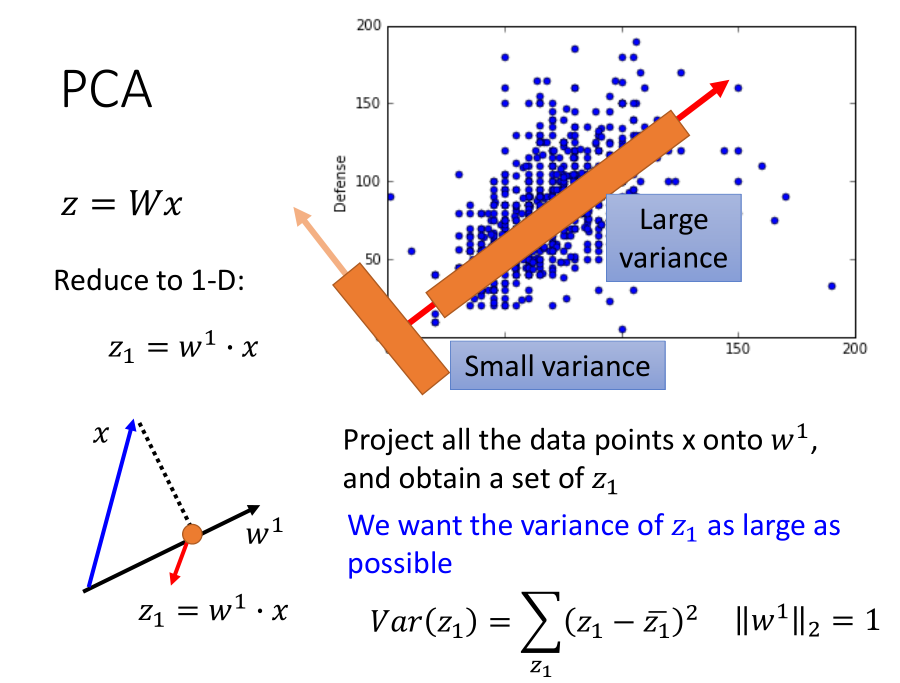
假设z是一维数据,假定 $||w^1||_2 = 1$,此时 $w^1x$ 表示 x 在 $w^1$ 上的投影;
目标:找到的 w 使得样本投影在这一向量上的点的分布方差最大,如图,我们选择 Large variance 这一向量。
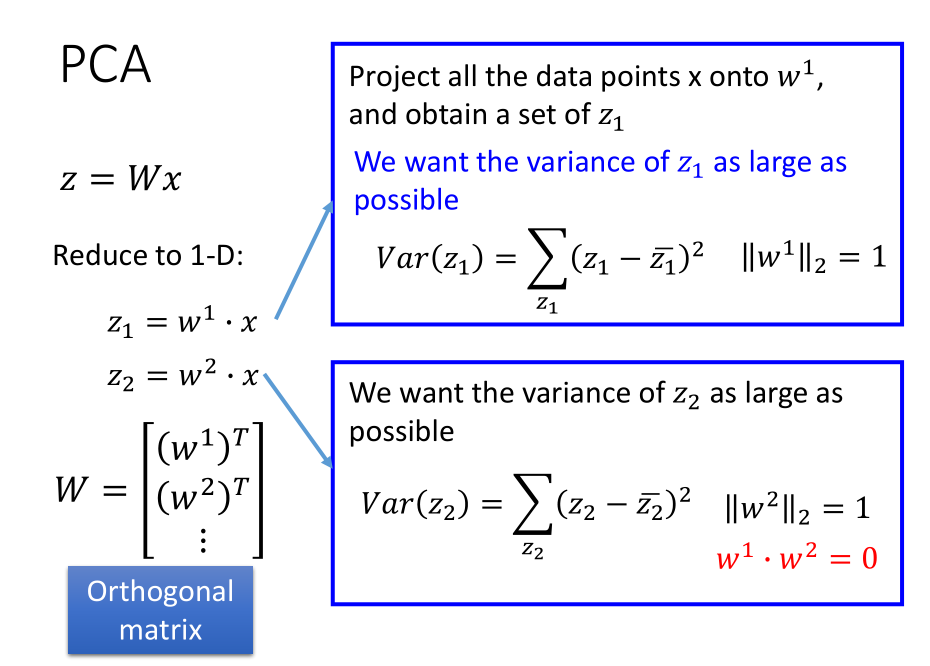
现在考虑高维情况,此时同样的思路也是找到相互垂直的 $w^1,w^2…w^K$ ,使得 $z^1,z^2…z^K$ 分布方差最大。
5.2 PCA数学推导部分

经过一系列的数学推导,最后目标函数转化为如下形式:
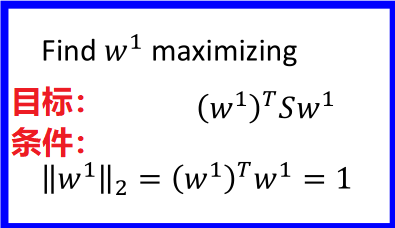

在求解的过程中:只需要知道上图中红色方框的结论即可:
$w^1$是协方差矩阵S的特征向量;并且与其相对应的最大特征值$\lambda_1$
同理计算 $w^2$

结论:
$w^2$ 是协方差矩阵 S 的特征向量;并与其第二大特征值 $\lambda_2$ 相对应
5.3 PCA
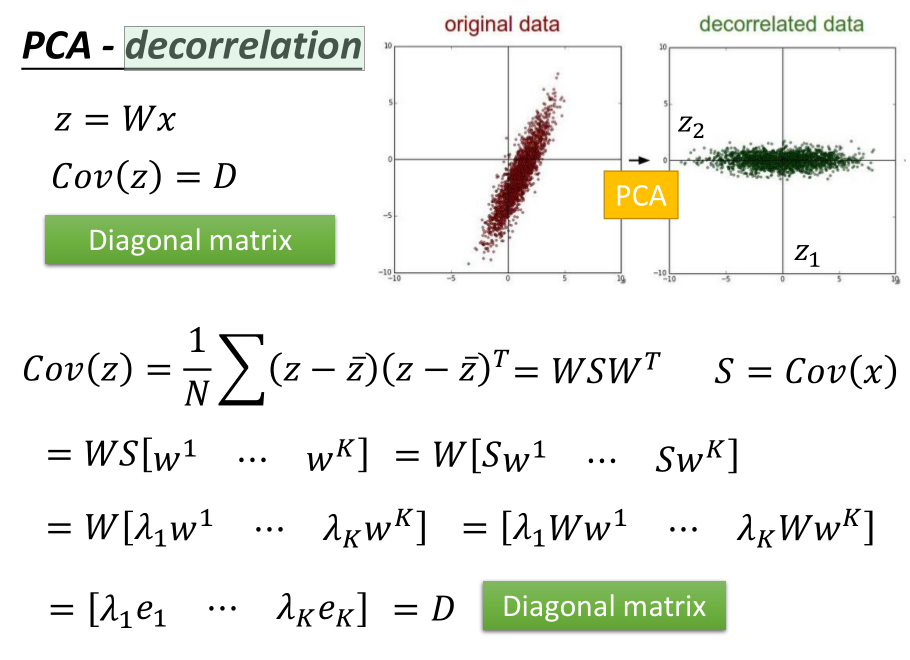
降维之后的 z 之间彼此是互相垂直的( cov(z) 是一个对角矩阵),
由此得出的结果再作为其他模型的输入,可以大大减少模型的参数。
5.4 SVD 对 PCA 进行求解
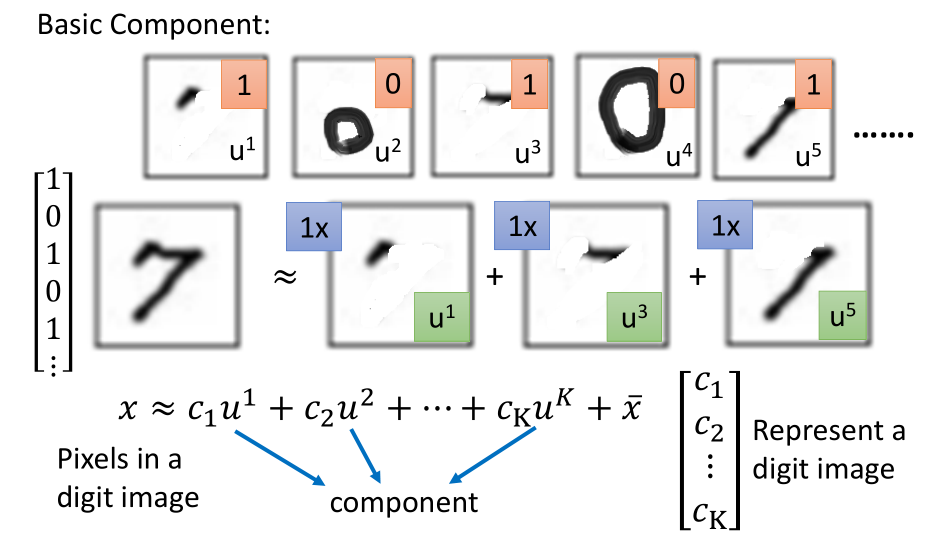

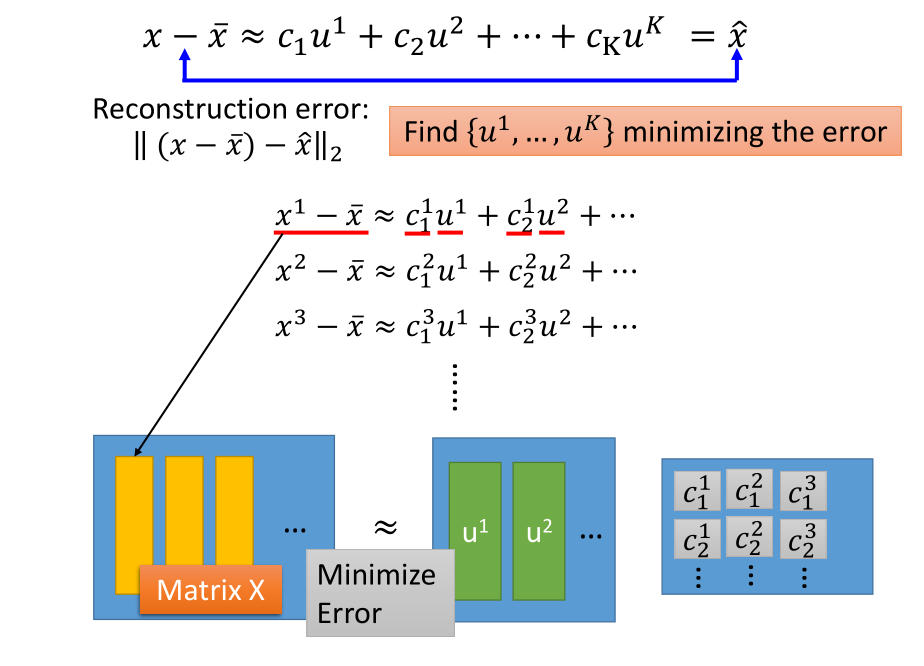
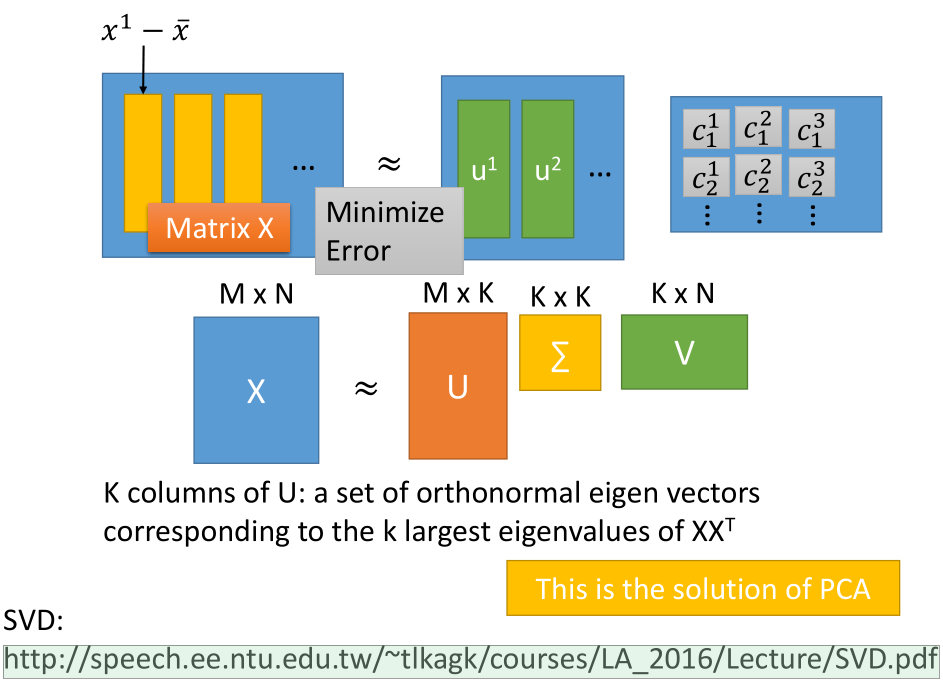
U 的 K 列:$XX^T$的 K 个最大特征值对应的一组标准正交特征向量
$\sum$:$XX^T$ 的非负特征值
SVD 矩阵分解知识:
http://speech.ee.ntu.edu.tw/~tlkagk/courses/LA_2016/Lecture/SVD.pdf
5.5 从 NN 角度理解 PCA
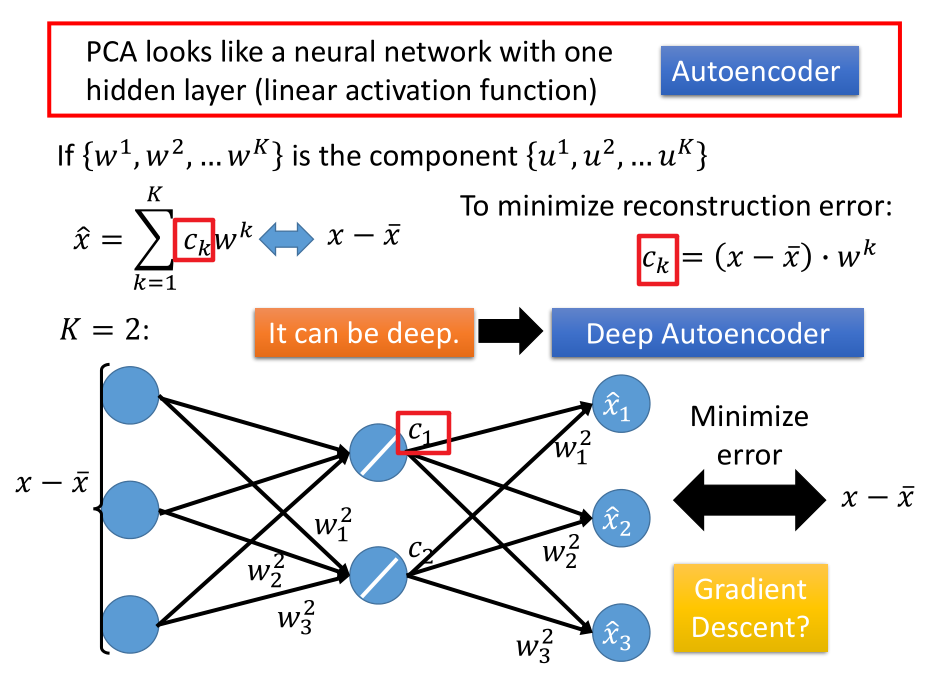
训练这个NN的参数,让输入和输出越接近越好。
不能用 gradient descent ,因为不能保证 $w^i,w^j$ 正交。
效果也不会比 SVD 方法更好。
5.6 PCA的缺点

- PCA 是无监督的,不知道数据的标签,这样在降维映射之后可能会把两类数据混到一起。
考虑数据标签的方法 LDA(Linear Discriminant Analysis)可以避免这一问题。 - PCA 是线性的。把一个三维空间中的S形分布的数据做 PCA 之后的效果,就是把 S 形拍扁,而非展开。
5.7 PCA 实例化
- 对宝可梦做PCA

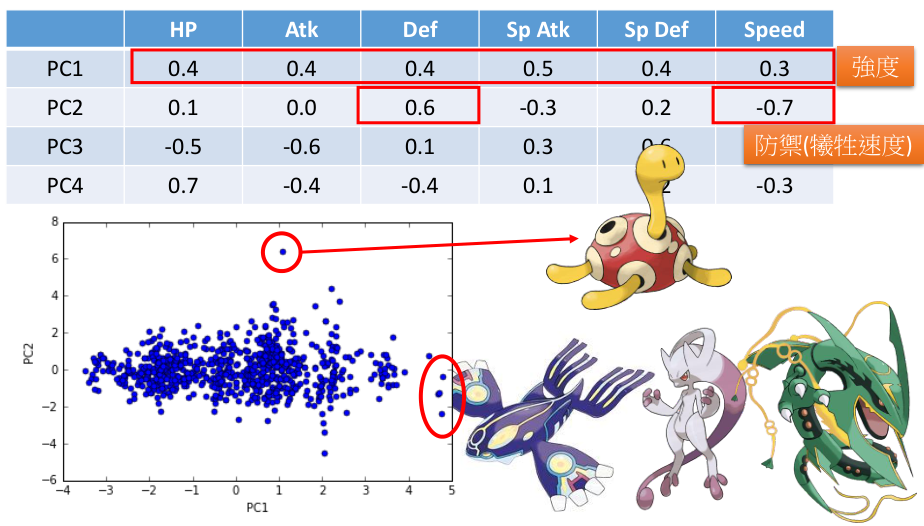
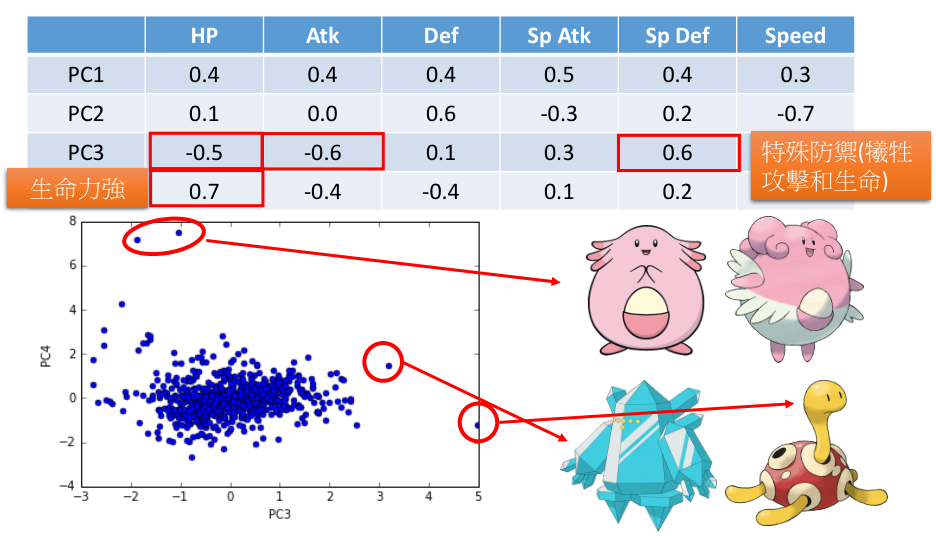
每个宝可梦是六维向量,计算出6个特征值,计算6个特征值的 ratio ,
舍去较小的(只取前四个特征值的特征向量作为新的特征)
特征值的意义是, PCA 降维时,在相应维度的 variance 有多大。
每个 PC 都是一个六维向量,分析它们在哪个维度是大的正值/负值,
可以分析出这个 PC 所代表的意义。
- PCA-MNIST

对手写数字识别,取前30个 PC ,如上图:
白色部分代表有笔画,前面看起来比较清晰,后面就比较复杂。
- PCA-Face
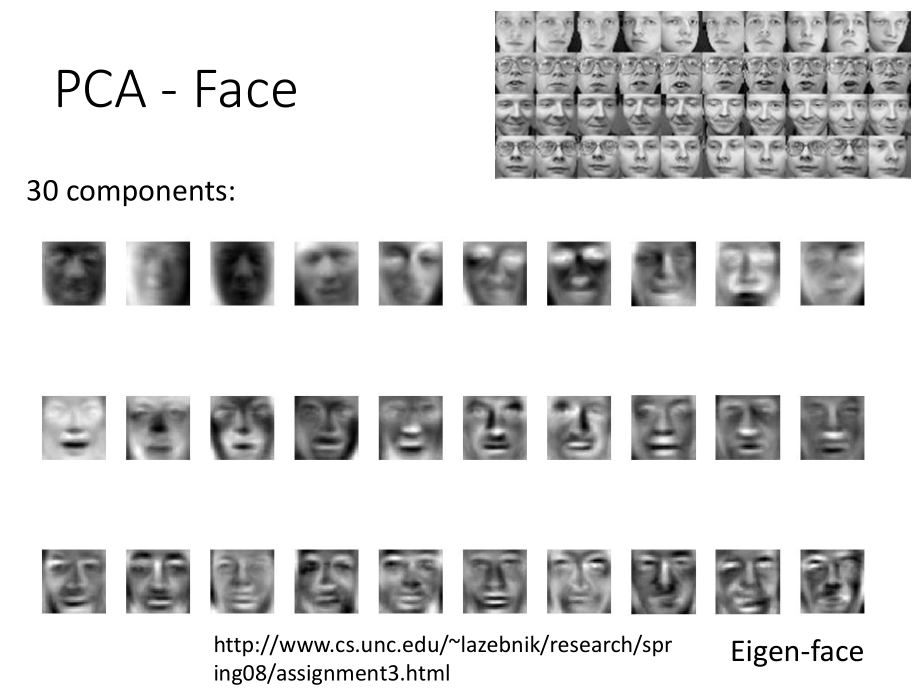
对人脸,取前30个 PC ,每个 PC 拼成图片,发现都是脸,而不是脸的一部分。
5.8 What happens to PCA?

- 对数字和人脸做NMF
此时得到的都是“部分”:


6. 矩阵分解
人买公仔,人和公仔背后都有共同的隐藏属性影响人买多少公仔,例如:
人的属性:萌傲娇/萌天然呆;公仔的属性:傲娇/天然呆。
我们要从购买记录(矩阵)中推断出 latent factor ,latent factor 的数目需要事先定好。
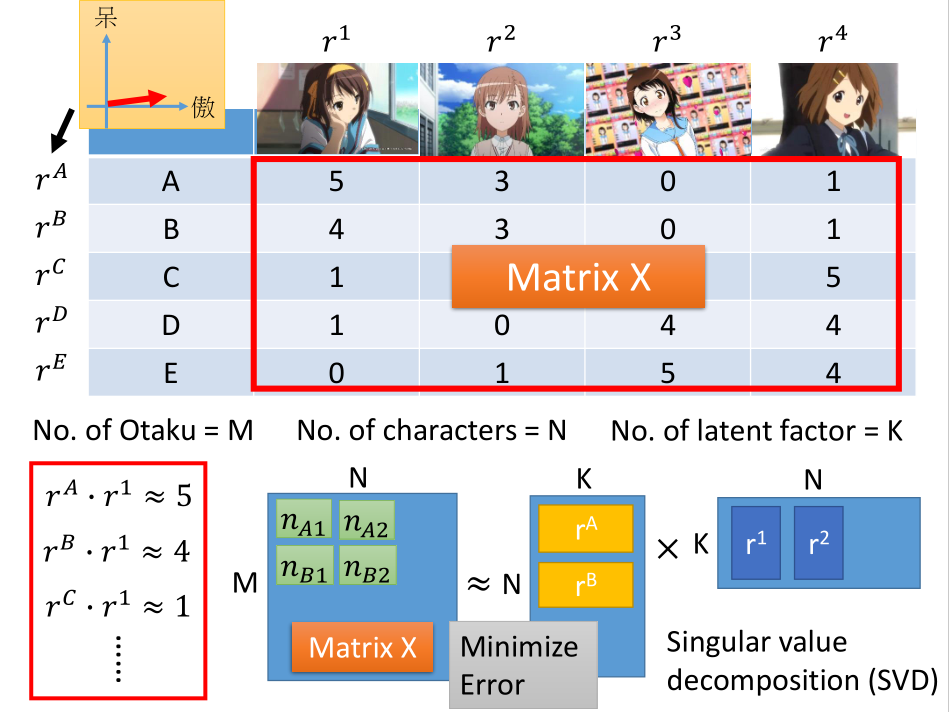
[注意]:矩阵分解的第一个矩阵应该为 M X K
对矩阵进行 SVD 分解, SVD 分解后的矩阵 $\sum$ 并入左边或者右边都可以。
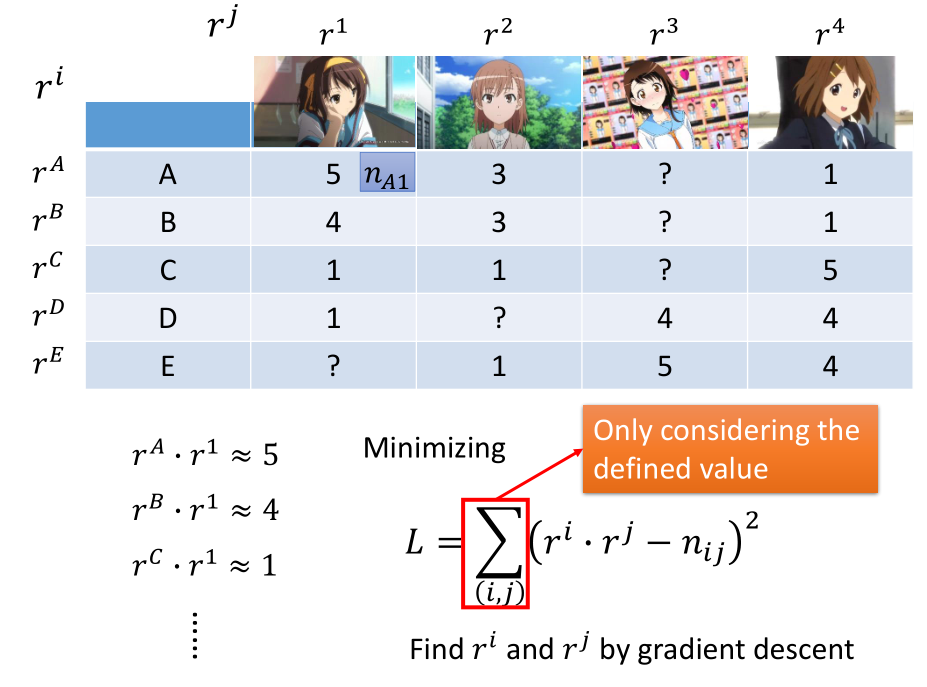
对缺失值的处理(missing data):
先定义 loss function L(只考虑有定义的数据),用 gradient descent 实现。
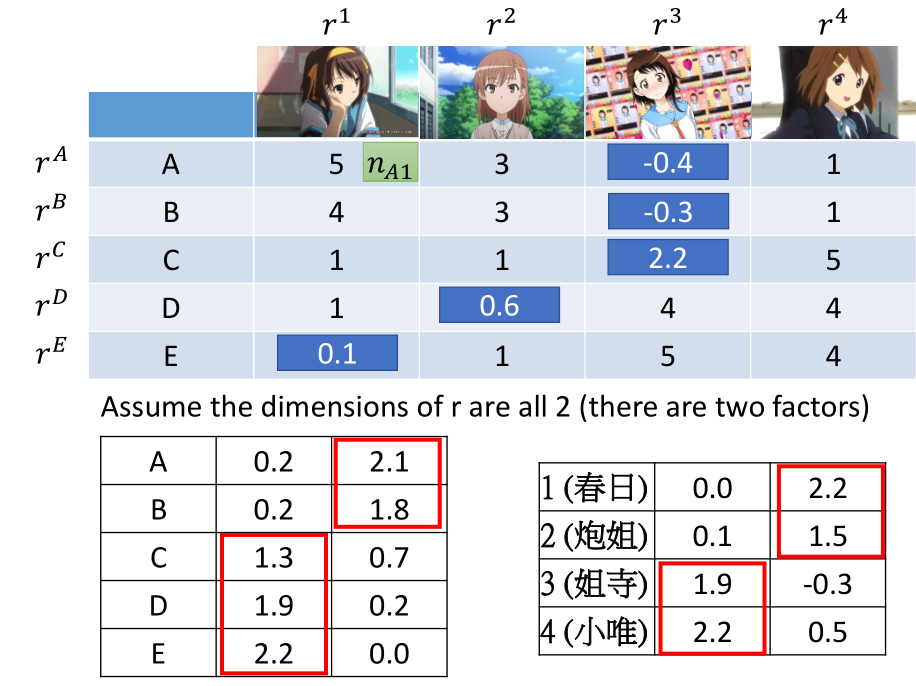
得到$rA,rB,rC,rD,rE,r1,r2,r3,r4rA,rB,rC,rD,rE,r1,r2,r3,r4$ 之后,并不知道每个维度代表什么属性,需要事后分析。
已知姐寺与小唯属于天然呆类型、春日与炮姐属于傲娇类型,所以第一个维度代表天然呆,第二个维度代表傲娇。

$b_A$:表示 A 购买公仔的喜欢程度;与属性无关
$b_1$:表示公仔1被购买的程度;与属性无关
参考资料:http://www.quuxlabs.com/blog/2010/09/matrix-factorization-a-simple-tutorial-and-implementation-in-python/
7. 作业:对主题分析进行矩阵分解

