这节我们主要学习

• 结构化线性模型的三个问题

1.结构化线性模型

1.1 问题1

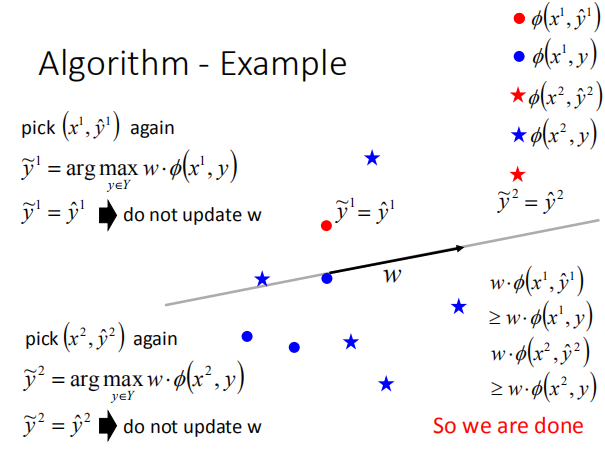
$F(x,y)$ 长什么样子：

将$ F(x,y) $表示成上图的形式，$ \phi_1 (x,y) $,$ \phi_2 (x,y) $,$ \phi_3 (x,y) $表示$ x,y $特征1,2,3的强度值；

$ F(x,y) $依旧是$ x,y $的函数，$ w_1,w_2,w_3 $通过学习数据得到

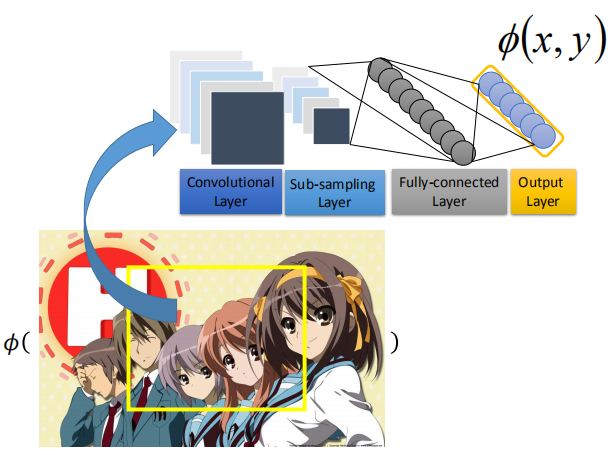
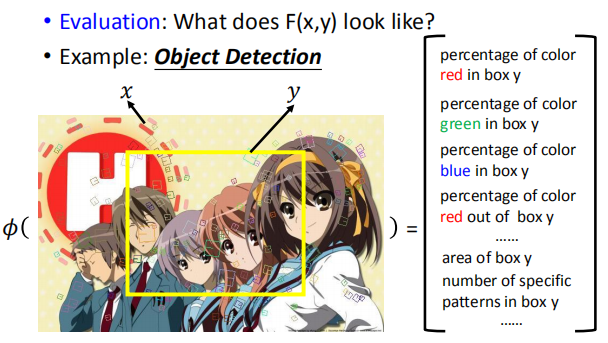我们使用深度学习来抽取特征；在目标检测中，我们使用卷积神经网络来得到$\phi (x,y)$

1.2 问题2

如何解决$arg$ $max$问题：

我们先假设问题2已经被解决

1.3 问题3

给出训练数据，如何学习$ F(x,y) $

• $F(x,y)=w*\phi(x,y)$,我们需要做的就是学习$w$

我们希望训练数据集中的$ w\phi(x^r,\hat y^r) $ 大于不正确的标签得到的值 $w\phi(x^r, y^r)$

红色点表示训练数据得到的特征值，在图中由红色边界框表示。

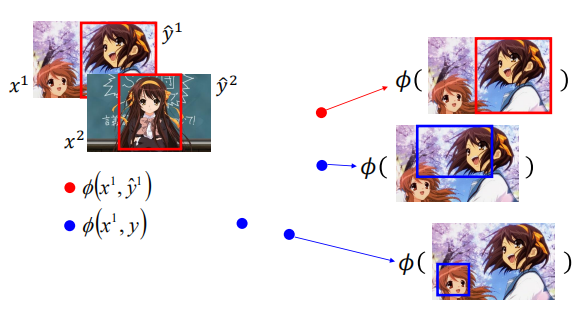
如图，点符号和星星符号分别表示不同的数据点；

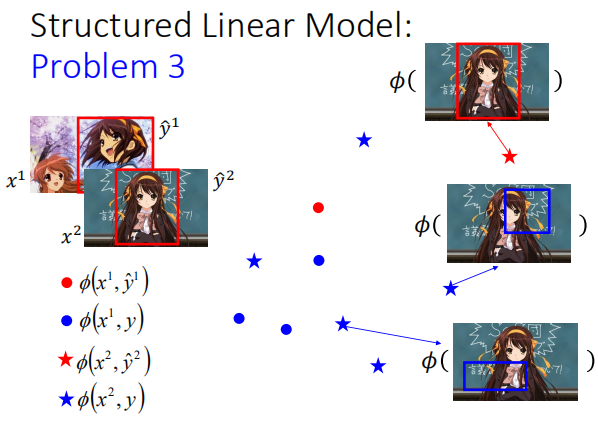
我们需要找一个$w$,使红色标记点的特征值与$w$点积的结果比对应的蓝色标记点的都大

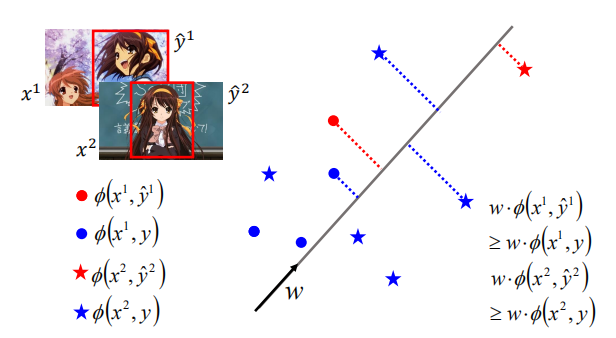
• do
  • 循环每一个训练数据
    • 我们都要找到使$ w*\phi(x^r,y) $最大的标签$ \tilde y^r $
  • if(求得的标签值与训练集数据给定的标签值不同)
    • $w \rightarrow w+\phi(x^r,\hat y^r)-\phi(x^r,\tilde y^r)$
• while($w$不再变化)

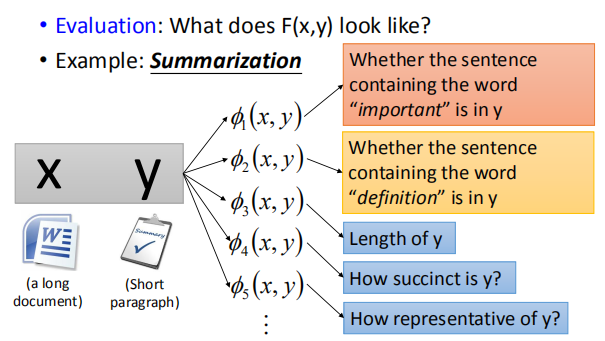
对于第一个训练数据点，因为初始化$w=0$,

所以我们随意选择一个$y$作为$\tilde y^1$,然后更新$w$

接下来针对第二个训练数据进行更新$w$

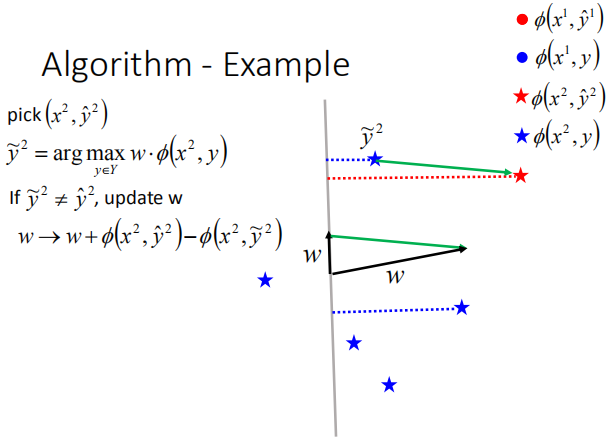
经过一次循环之后，我们发现$\hat y^1=\tilde y^1$, $\hat y^2=\tilde y^2$

此时任务完成，不需要再进行更新。