这节我们主要学习

• 集成学习介绍
• Bagging
• Boosting
• Stacking
• AdaBoost

1. 集成学习介绍

集成学习能够让你只对模型稍加修改就可以得到更好的结一个结果

集成学习的架构

• 获取一系列的分类器
  • $f_1(x),f_2(x),f_3(x),…$
• 将这些分类以某种合适的方式聚在一起

相当于打组团打 boss 一样需要合理的人员配置，例如坦克，辅助和输出。三者形成互补状态，达到整体强度最高。

2. Bagging 方法

2.1 方差与偏差

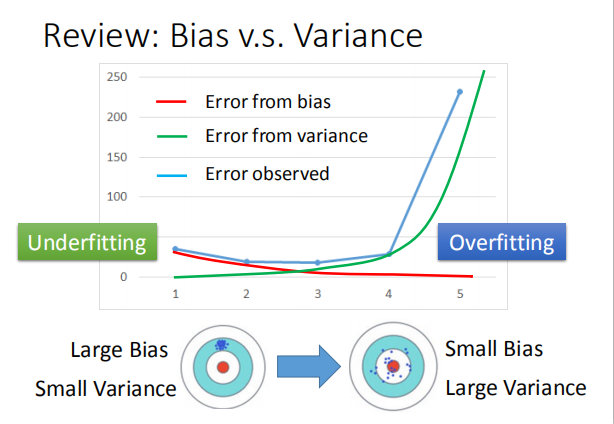
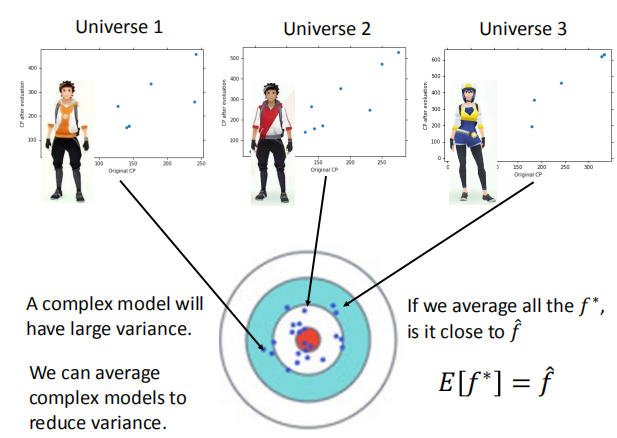
复杂的模型将有较大的方差;我们将所有的模型平均，

得到新模型 $f^*$ ,新的模型可能和正确答案很接近。

2.2 Bagging 的优点

对原始数据集进行采样，得到新的不同的数据子集，

再对这些新的数据集进行训练，得到不同的模型。

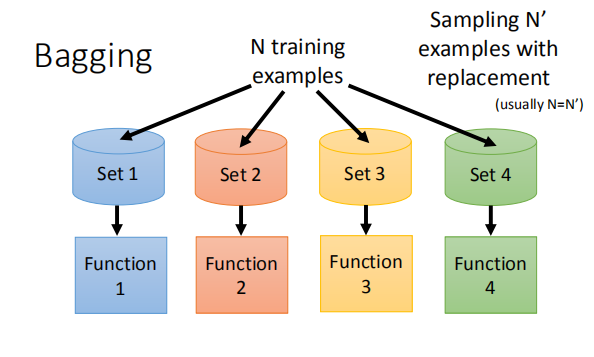
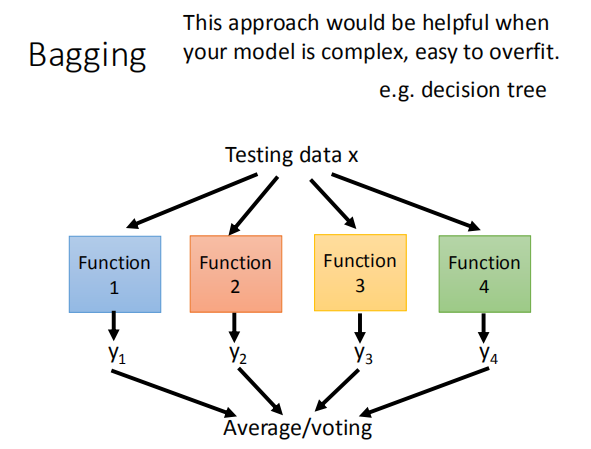上图表示了用自己采样的数据进行Bagging的过程。
在原来的N笔训练数据中进行采样，过程就是每次从N笔训练数据中取N‘（通常N=N’）
建立很多个dataset，这个过程抽取到的可能会有重复的数据，
但是每次抽取的是随机形成的dataset。每个dataset都有N’笔data，
但是每个dataset的数据都是不一样的，
接下来就是用一个复杂的模型对四个dataset都进行学习得到四个function，
接下来在testing的时候，就把这testing data放到这四个function里面，
再把得出来的结果做平均（回归）或者投票（分类），
通常来说表现（variance比较小）都比之前的好，这样就不容易产生过拟合。
做Bagging的情况：模型比较复杂，容易产生过拟合。
（容易产生过拟合的模型：决策树）目的：降低方差

3 决策树

用决策树来解决分类问题：

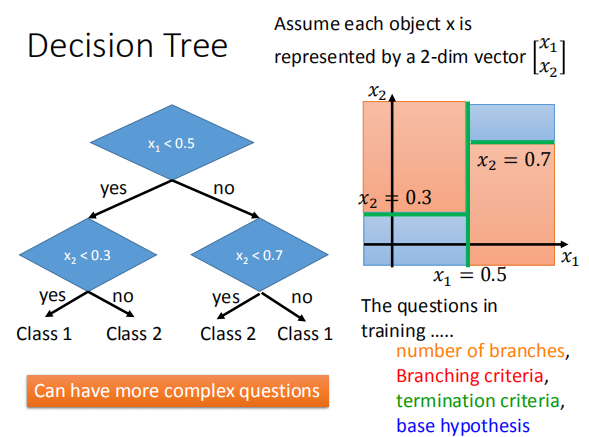
实验：二元分类问题

实验条件：单一决策树

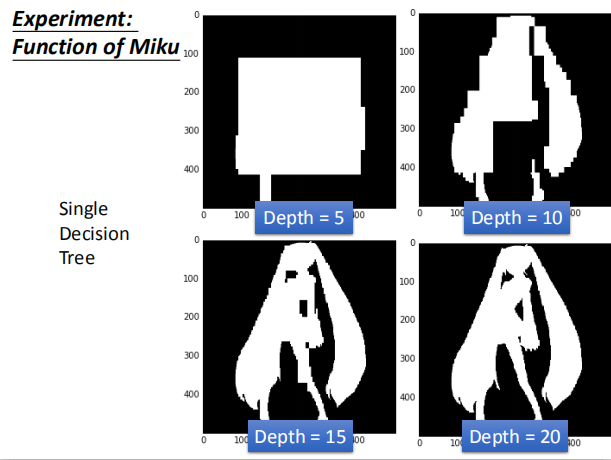随着决策树深度的增加，分类的标准越来越多，边界值也越来越明显，实验结果越来越好。

4 随机森林

• 决策树：
  • 易于实现训练数据错误率为 0%
  • 如果树的每一个分支对应一组训练数据的话，正确率将达 100%
• 随机森林：
  • 仅仅重新采样训练数据是不够的
  • 随机限制每个拆分中使用的特征/问题
• 袋装验证：
  • 使用不同的模型去测试数据集，袋装误差能够很好的预测测试集误差

实验结果：

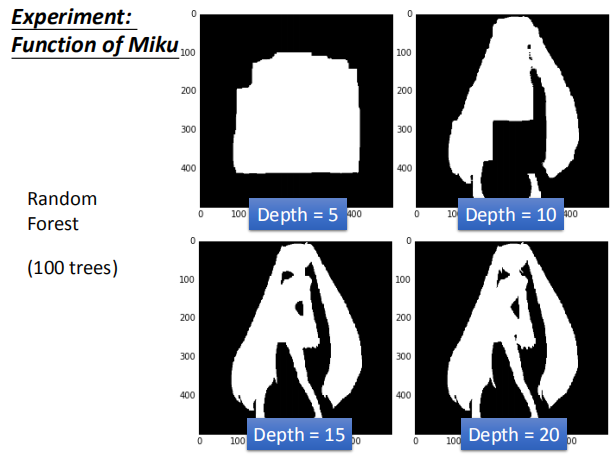
5 Boosting

• 条件和目标：
  • 如果机器学习算法可以在训练数据上生成错误率小于 50% 的分类器，
  • 增强后，错误率可以降低到 0%
• boosting 的框架：
  • 获取第一个分类器 $f_1(x)$
  • 找到另外一个函数 $f_2(x)$ 来改良 $f_1(x)$
    • 我们希望 $f_1(x)$ 和 $f_2(x)$ 互补
  • 得到第二个分类器 $f_2(x)$
  • $…$ 最后,合并所有分类器

• 分类器按顺序被学习

• 在不同的训练集上进行训练
• 怎样拥有不同的训练集
  • 重新采样训练数据以形成新的数据集
  • 重新加权训练数据以形成新的数据集
  • 在实现过程中,只需要更改变损失（目标）函数

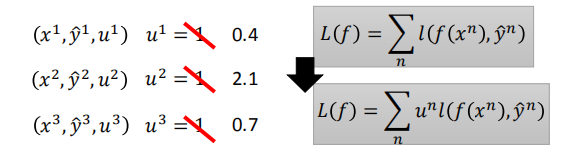例如，系数$u^2$越大，则更新参数时就会更加考虑拟合该数据（$x^2$，$y^2$）。

6 AdaBoost

6.1 介绍 AdaBoost

• 思想：在$f_1(x)$失效的数据集上训练$f_2(x)$
• 如何找到使$f_1(x)$失效的数据集呢？

原始数据集经过训练后，经过 $f_1(x)$ 时错误率很容易就可以达到小于 0.5，
为该数据集分配新的权重 $\mu^n_2$，使错误率达到 0.5。
错误率在 0.5 时，直观上可以感受到 $f_1(x)$ 与随机分类的效果没多大差别，
此时利用该权重训练得到的新的 $f_2(x)$，此时 $f_1(x),f_2(x)$ 就会形成互补。

为训练集数据重新分配权重：

如果该数据分类错误，将权重乘以 $d_1$；若分类正确，权重除以 $d_1$。（由于要增加错误所造成的权重，$d_1$ 取值会大于1）

求解 $d_1$ 的过程：

直观上的结果是预测与结果一致的新的权重之和与预测错误的权重相等各占 0.5，
当然可以可以令错误率等于 0.5，进行反解表达式得到更新公式。

6.2 AdaBoost 算法

对于给定的训练集，通过 T 次循环，计算出 T 个分类器。

如何将它们聚合起来？

当该模型的错误率越小时，我们给该模型分配的权重越大。（表示我们更偏向于相信该模型的结果）

6.3 Toy 实例

分类器的训练过程：

我们需要使用弱分类器。

由第一幅图可知，第一次分类有 7 个正确，左边两个蓝色的类别和右边五个红色的类别，
然后更新权重，使右边蓝色的错误分类放大为 1.53，可得 7*0.65 约等于 3*1.53，即错误率约等于 0.5，
此为第一次更新，然后重复更新权重和分类方法。

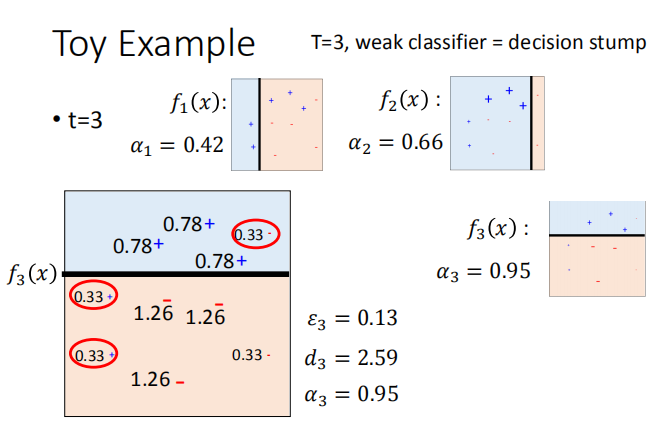
最终整个模型的准确率为 100%

6.4 AdaBoost证明推导

当T越大，迭代次数越多时，$H(x)$ 在训练集上的错误率越来越小

模型最终的错误率有一个上界，始终 $\leq$ $\sum_n exp(-\hat y^n g(x^n))$

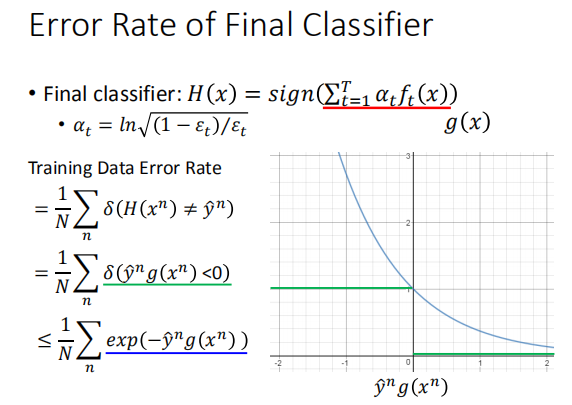
$Z_t$ 为训练集数据的权重的总和；经过一系列的数学推导，得到 $Z_{T+1}$ 的表达式；

联立训练集错误率的表达式，得到

Error Rate $\leq \sum_n exp(-\hat y^n g(x^n))$ = $\frac{1}{N}Z_{T+1}$

由上图可以得出，$Z_T$ 随着 $T$ 的增大不断减小，

所以，当 $T$ 增大时，错误率的上界不断减小，错误率大概率跟着不断减小。

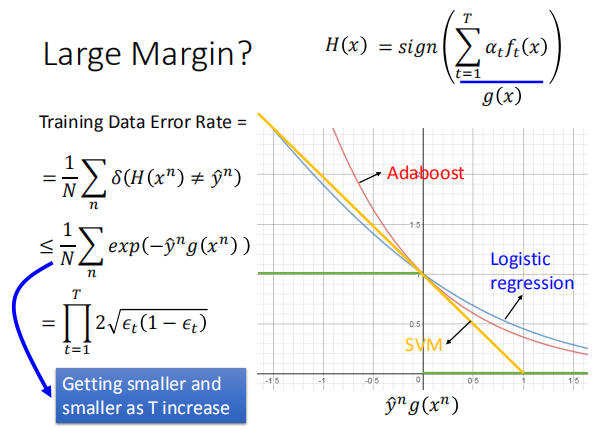
6.5 AdaBoost的神秘现象

当T增大到一定程度时，会发现训练集误差率已经降为 0 不发生改变，但是

测试集的误差率还是会一直减小。

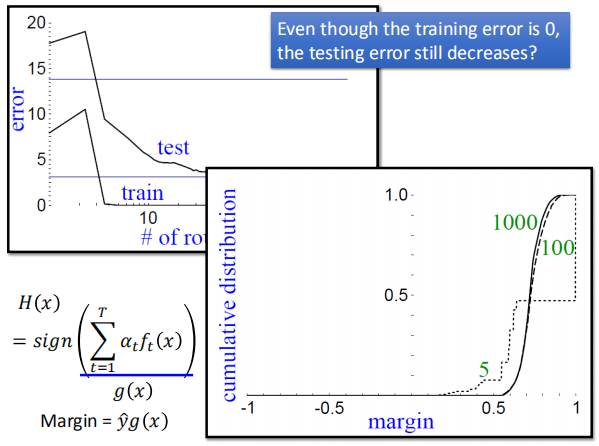定义间隔 Margin = $\hat y g(x)$;当迭代次数较多时，间隔会增大，使得模型在

测试集上的表现更好。（当训练集的错误率为0时，$\hat y g(x)$ 始终同号，即始终大于 0）

6.6 AdaBoost + 决策树 做初音的实例

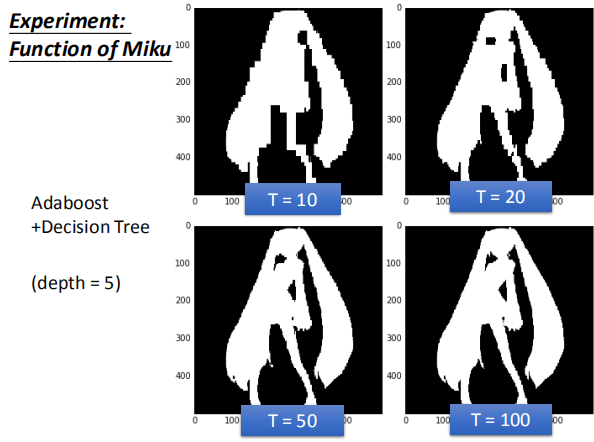当树的深度一定时，迭代的次数越多错误率越低，模型的效果越好。

7. Gradient Boosting

建立模型的一般步骤：

初始化一个模型，不断的迭代不断的优化，使目标函数最小化，得到最后的模型

Gradient Boosting是Boosting的更泛化的一个版本。 具体步骤：

• 初始化一个$g_{0}(x)=0$,
  
• 进行很多次的迭代，找到一组$f_t(x)$和$\alpha_t$来共同改进$g_{t-1}(x)$
  
• $g_{t-1}(x)$就是之前得到所有的f(x)和$\alpha$乘积的和
  
• 把找到的一组$f_t(x)$和$\alpha_t$（与$g_{t-1}(x)$互补）加上原来的$g_{t-1}(x)$得到新的$g_{t}(x)$，这样$g_{t}(x)$就比原来的$g_{t-1}(x)$更好
  
• 最后再得到T个迭代的H(x) 这里的cost function是$L(g)=\sum\limits_{n}l(\hat{y}^n,g(x^n))$,
  其中ll是$\hat{y}^n$ 和$g(x^n)$的差异（loss function，这个函数可以直接选择，可以是交叉熵，也可以是均方误差）
  这里定义成了$exp(-\hat{y}^ng(x^n))$
  
• 接下来我们要最小化损失函数，我们就需要用梯度下降来更新每个g(x)
  

我们希望用梯度下降求得部分和用 AdaBoost 求得部分的方向越一致越好。

在最大化的过程中，我们求得的 $f_t(x^n)$ 和用 AdaBoost 求得 $f_t(x^n)$ 是一致的。

在求出 $f_t(x^n)$ 之后，我们希望求得一个 $\alpha_t$ 使得损失函数最小

这里找出来的$f_t(x)$，其实也就是AdaBoost找出来的$f_t(x)$,
所以在AdaBoost的时候，找一个弱的分类器$f_t(x)$，就相当于用梯度下降更新损失，值得损失会变小。
由于求$f_t(x)$是很不容易才找到的，所以我们这里就会给$f_t(x)$配一个最好的$\alpha_t$，把$f_t(x)$的价值发挥到最大。

对于$\alpha_t$就很像学习率，但是这里有点不一样，我们是固定$f_t(x)$，
穷举所有的$\alpha_t$找到一个$\alpha_t$使得$g_{t}(x)$的损失更小
实际中就是求解一个最优化问题，找出一个$\alpha_t$，让$L(g)$最小。

巧合的是找出来的$\alpha_t$就是$\alpha_t=ln\sqrt{(1-\epsilon_t)/\epsilon_t}$
AdaBoost其实可以想成在做梯度下降，只是这个梯度是一个函数，
然后有一个很好的方法来决定学习率的这样一个问题。
Gradient Boosting有一个好的就是我们可以任意更改目标函数。
这样就可以创造出很多新的方法。

8. Stacking

在集成多个模型之后，我们需要再添加一个最终的分类器，

为每一个模型分配一个合适的权重。

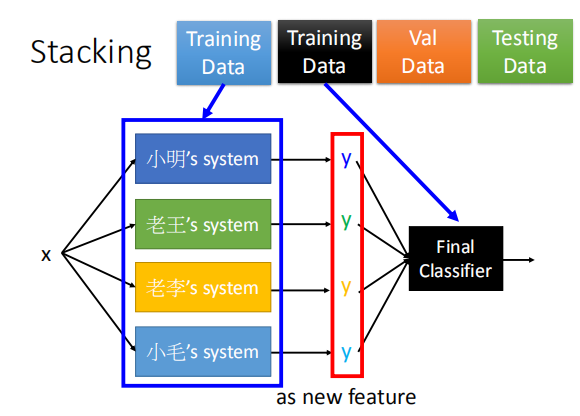
我们将训练集的数据分为两个部分，一部分用于训练各个模型，

另一部分用于训练最后的分类器，两部分数据没有重叠。

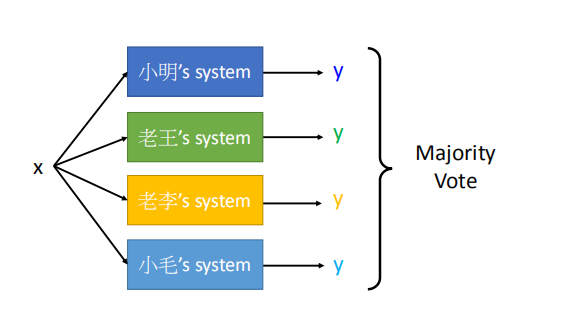
上图中，把一笔数据x输入到四个不同的模型中，然后每个模型输出一个y，然后用投票法决定出最好的（对于分类问题）
但是有个问题就是并不是所有系统都是好的，有些系统会比较差，
但是如果采用之前的设置低权重的方法又会伤害小毛的自尊心，
这样我们就提出一种新的方法：
把得到的y当做新的特征输入到一个最终的分类器中，然后再决定最终的结果。
对于这个最终的分类器，应当采用比较简单的函数（比如说逻辑回归），不需要再采用很复杂的函数，因为输入的y已经训练过了。
在做stacking的时候我们需要把训练数据集再分成两部分，一部分拿来学习最开始的那些模型，另外一部分的训练数据集拿来学习最终的分类器。
原因是有些前面的分类器只是单纯去拟合training data，
比如小明的代码可能是乱写的，他的分类器就是很差的，他做的只是单纯输出原来训练数据集的标签，
但是根本没有训练。如果还用一模一样的训练数据去训练最终分类器，这个分类器就会考虑小明系统的功能。
所以我们必须要用另外一部分的数据来训练最终的分类器，然后最终的分类器就会给之前的模型不同的权重。