这一节我们主要学习

• 梯度下降法
• 链式法则
• 前向传播
• 反向传播

1.基础知识

1.1 梯度下降算法

• 网络的参数$θ=$ {$w_1,w_2,…,b_1,b_2,..$}

• 起始参数： $θ^ 0 \longrightarrow θ^ 1 \longrightarrow θ^ 2 \longrightarrow …… $

• 在神经网络使用梯度下降算法求解最优化的损失函数，反向传播算法能够使梯度计算更高效。

1.2 链式法则

• 因为神经网络有着多个隐藏层，所以在计算偏导数的过程中要使用到链式求导法则。

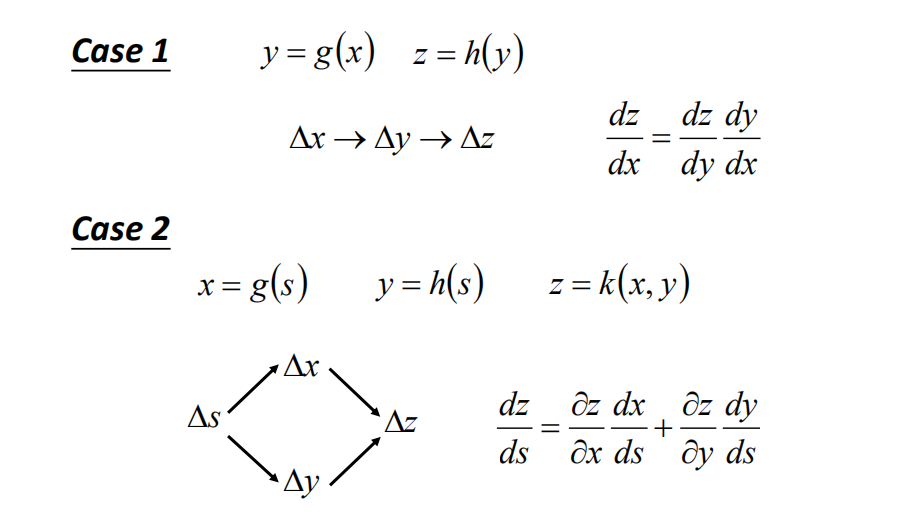
2.反向传播算法

2.1 梯度计算

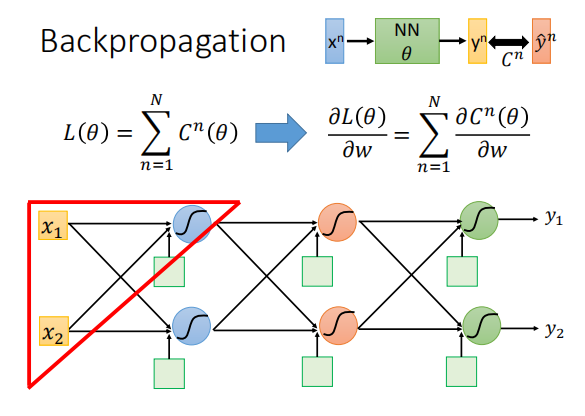
• 我们要最小化的损失函数 L(θ) 是每一组数据的损失 C(θ) 之和。（注：这里的 C(θ) 对应视频中的 l(θ)）
• 因此计算 L(θ) 的偏微分等价于计算每一个 C(θ) 的偏微分，再将之加总。所以接下来算 C(θ) 的偏微分。

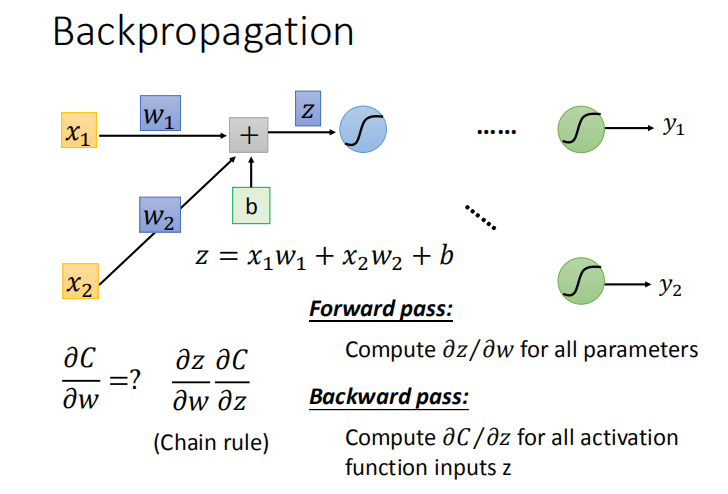
• 对第一层的某一个神经元进行分析发现：$\frac{\partial C}{\partial w} = \frac{\partial z}{\partial w} \frac{\partial C}{\partial z}$
• 前向传播阶段：计算所有参数的 $\frac{\partial z}{\partial w}$
• 反向传播阶段：计算所有参数的 $\frac{\partial C}{\partial z}$

2.2 前向传播

• 为所有的参数计算 $\frac{\partial z}{\partial w}$

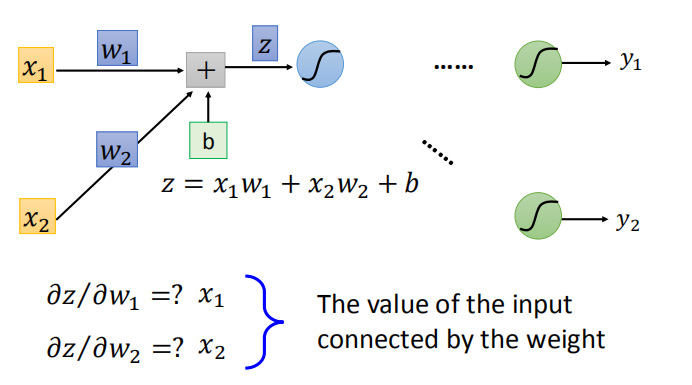
• 实例：

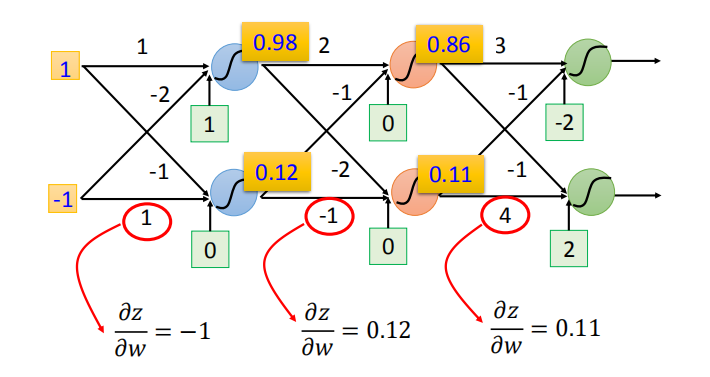
2.3 后向传播

• 计算 $\frac{\partial C}{\partial z} : \frac{\partial C}{\partial z} = \frac{\partial a}{\partial z} \frac{\partial C}{\partial a}$

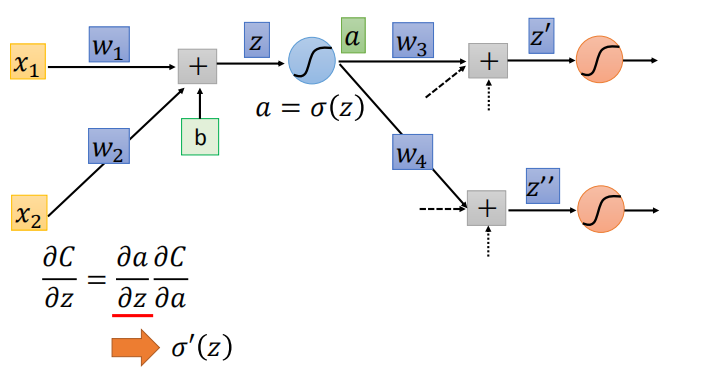
• 第一步，计算 $\frac{\partial a}{\partial z}= σ’(z)$ :

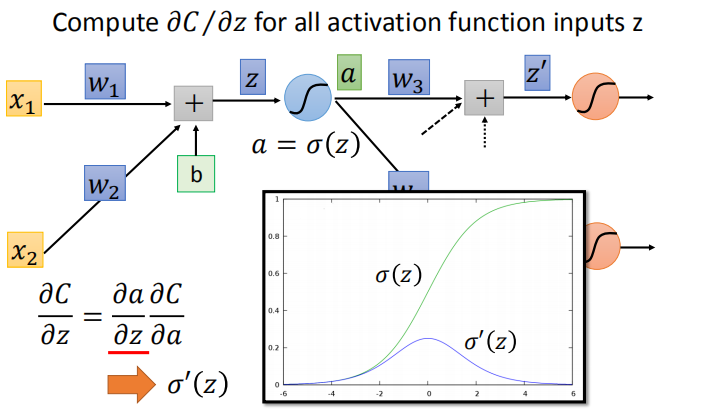
• 第二步，计算 $\frac{\partial C}{\partial a}$ :

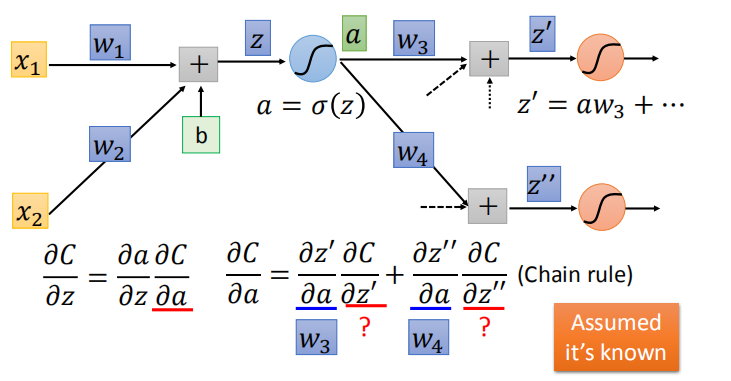
• 假设 $\frac{\partial C}{\partial z’}$ 和$\frac{\partial C}{\partial z’’}$ 已知,后向传播阶段的结果：

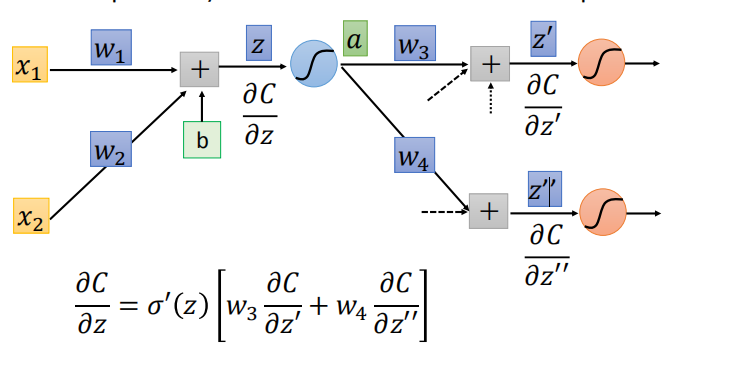
• 但实际$\frac{\partial C}{\partial z’}$ 和 $\frac{\partial C}{\partial z’’}$是未知的，接下来分两种情况进行讨论：

• 情况1：该层是输出层，$\frac{\partial C}{\partial z’}$ 和 $\frac{\partial C}{\partial z’’}$为输出层的输入

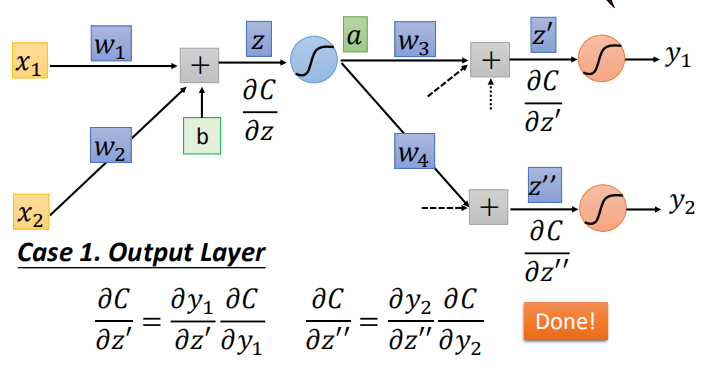
• 情况2：该层不是输出层，我们可以递归地计算，直到我们到达输出层。然后，从输出层不断向前计算，得到 $\frac{\partial C}{\partial z}$

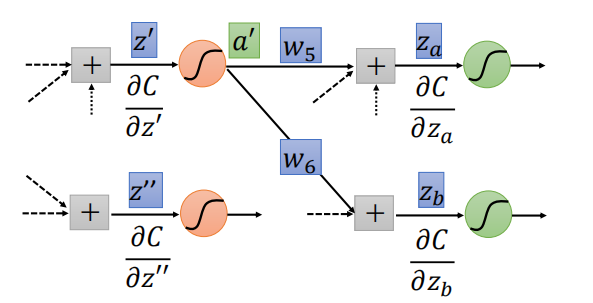
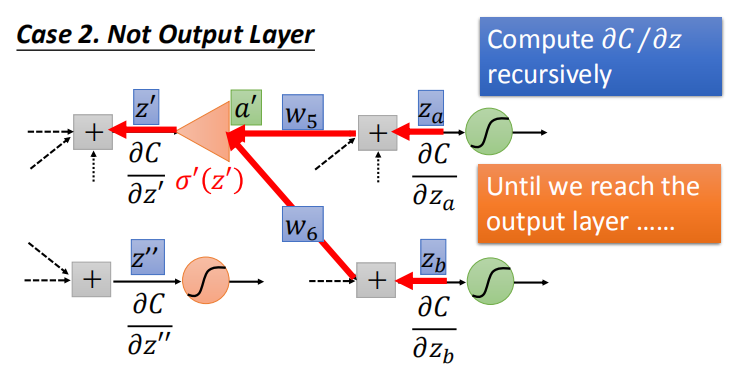
• 情况2： 从输入开始算感觉很麻烦，从输出开始算会发现和前馈网络运算量一样：

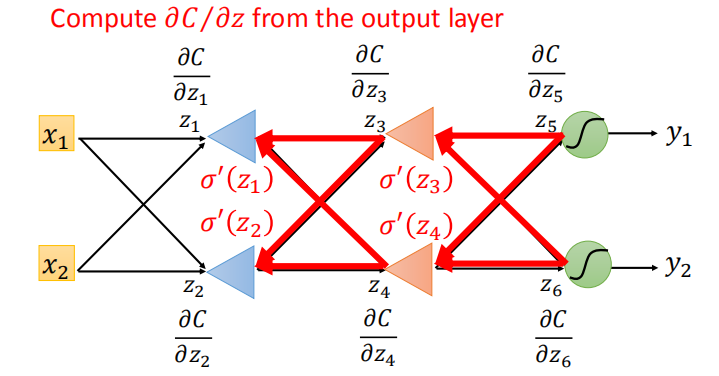
2.4 反向传播算法总结

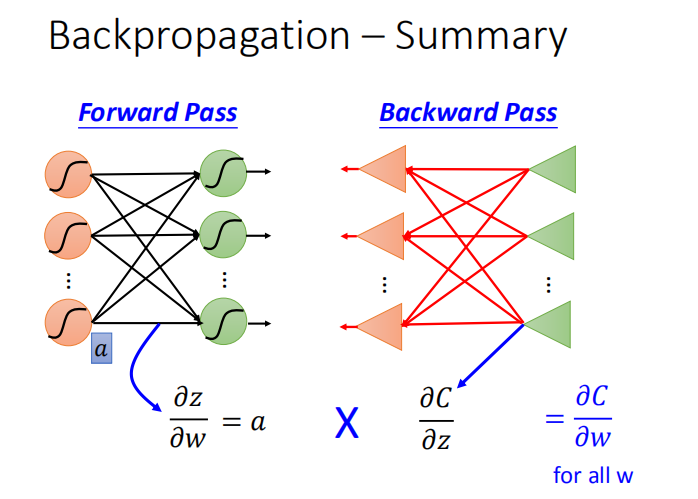
先做前向传播，计算出激活函数的输出$\frac{\partial z}{\partial w} = a$,
再从反向传播中求出$\frac{\partial C}{\partial z}$，将上述结果相乘即得到$\frac{\partial C}{\partial w}$