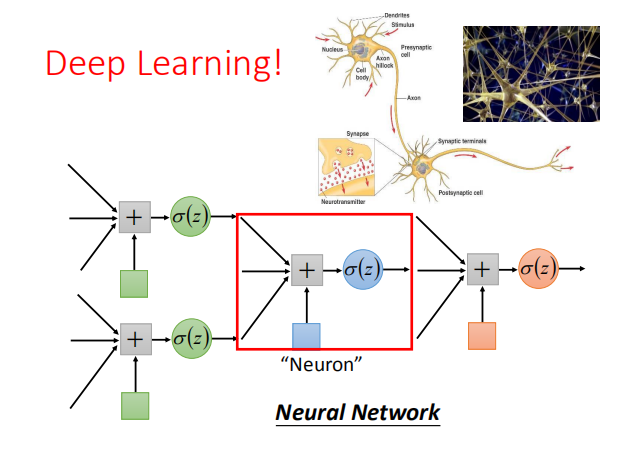
这一节我们主要学习

• 逻辑回归模型
• 逻辑回归与平方误差
• 判别模型 vs. 生成模型
• 多元分类
• 逻辑回归的局限性
• 延伸：深度学习

1. 建立逻辑回归模型

1.1 步骤1：确定函数集

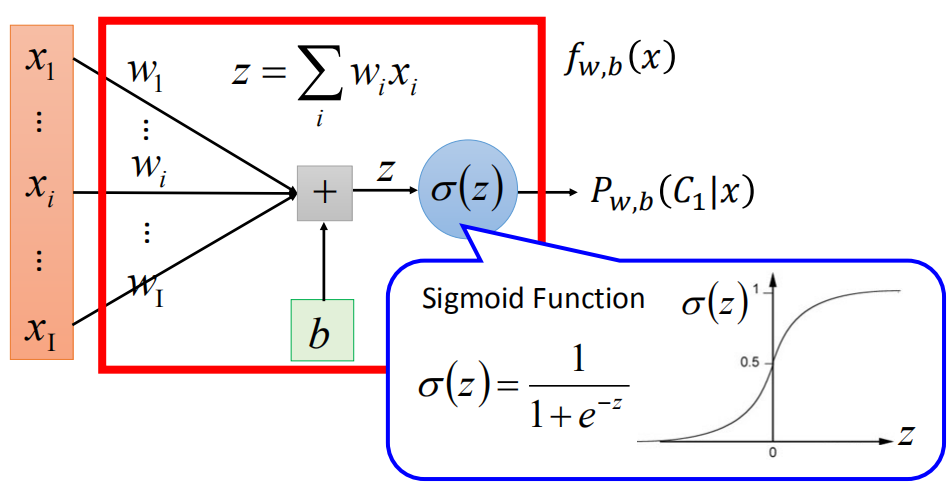
我们需要找到一个概率函数 $P_{w,b}(C_1|x)$ ，该函数有如下特征：

当 $P_{w,b}(C_1|x) \geq 0.5$  时，输出 $C_1$ ； 否则输出 $C_2$。

函数 $P_{w,b}(C_1|x) = σ(z)$ ， 满足上述条件。

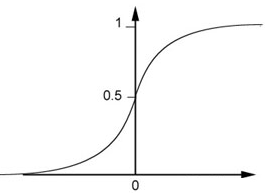
其中$z = wx + b，σ(z) = \frac{1}{1+exp(-z)}$ ，如图。

函数集 $f_{w,b}(x) = P_{w,b}(C_1|x)$ ，如图：

• 比较逻辑回归和线性回归：

  • 逻辑回归：$f_{w,b}(x) = σ(\sum_{i}w_ix_i+b)$ ； 输出范围(0 , 1)

  • 线性回归：$f_{w,b}(x) = \sum_{i}w_ix_i+b$ ；输出范围($-\infty$,$+\infty$)
    

1.2 步骤 2：模型评价

如图所示，假设训练数据集是依据 $f_{w,b}(x) = P_{w,b}(C_1|x)$ 产生的，给出一系列的 $w$ 和 $b$，产生该数据集的概率为多少？

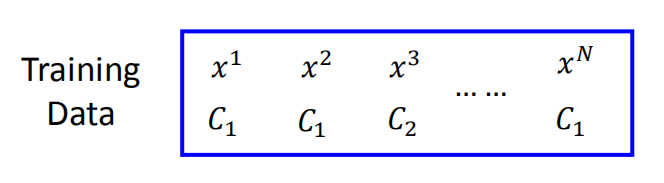
产生该数据集的概率为 $L(w,b) = f_{w,b}(x^1)f_{w,b}(x^2)(1-f_{w,b}(x^3)) \cdots f_{w,b}(x^N)$ （注意$x^3$属于$C_2$类别）

其中 $w^{*},b^{*} = arg maxL(a,b)$，当 $w$ 和 $b$ 分别取 $w^*,b^* $ 时，函数 $L(w,b)$ 取最大值。

$L(w,b)$的优化：

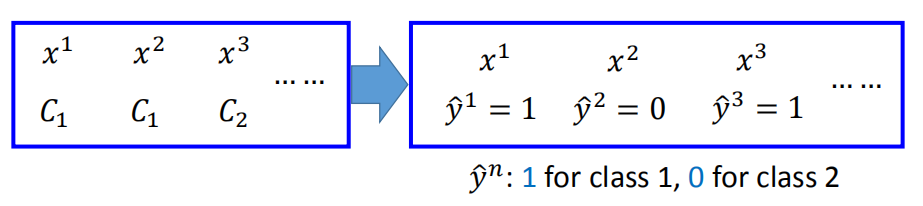
$L(w,b) = f_{w,b}(x^1)f_{w,b}(x^2)(1-f_{w,b}(x^3)) \cdots $

为简化计算，我们将求解 $L(w,b)$ 的最大值，转化为求解 $-lnL(w,b)$ 的最小值。

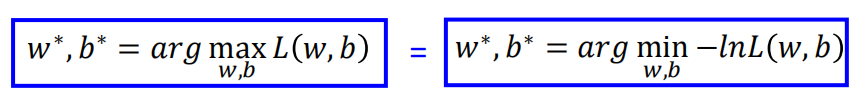
$-lnL(w,b)= \ln{f_{w,b}(x^1)}\ln{f_{w,b}(x^2)}\ln{(1-f_{w,b}(x^3))} \cdots$ = $\sum_{n=1}^{n=N} -[\hat y^{n}\ln{f_{w,b}(x^n)}+(1-\hat y^{n})\ln({1-f_{w,b}(x^n)})]$,

该函数可以看做两个伯努利分布之间的交叉熵，如图。

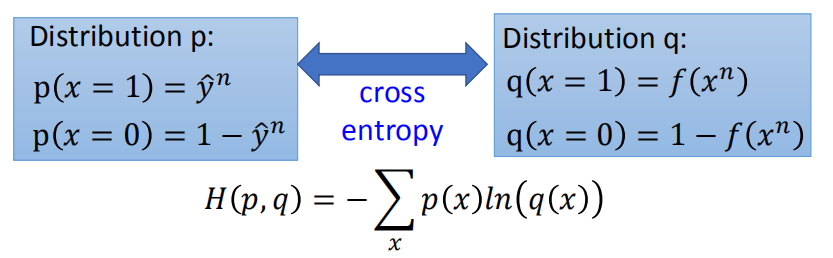
熵的概念本来是热力学的一个概念，描述物质的混乱程度。 在这里，我们用交叉熵的概念来描述两组不同概率数据分布的相似程度，越小越相似。

• 逻辑回归和线性回归训练集上的比较：

训练数据集($x^n,\hat y^{n}$)：

逻辑回归：$L(f) = \sum C(f(x^n),\hat y^{n})=\sum-[\hat{y}^nlnf(x^n)+(1-\hat{y}^n)ln(1-f(x^n))]$ 其中：$\hat y^{n}$ 取1表示分类1，取2表示分类2；

线性回归：$L(f) = \frac{1}{2}\sum (f(x^n)-\hat y^{n})^2$ ；其中$\hat y^{n}$ 表示一个真实有实际意义的值。

1.3 步骤3：模型优化

偏导数： $\frac{\partial (-lnL(w,b))}{\partial w_i}$ = $\sum_n-(\hat y^{n}-f_{w,b}(x^n))x_i^n$

梯度下降：$w_i \leftarrow w_i - 𝜂\sum_n -(\hat y^n - f_{w,b}(x^n))x_i^n$，由上式可以看出，偏差越大，更新的步长越大。

逻辑回归与线性回归在参数更新上的比较：

梯度下降表达式均为 $w_i \leftarrow w_i - 𝜂\sum_n -(\hat y^n - f_{w,b}(x^n))x_i^n$。

1.4 逻辑回归与回归模型总结对比

2. 逻辑回归与平方误差

• 步骤1：

$f_{w,b}(x) = σ(\sum_i w_ix_i+b)$

对线性回归中的加速函数 $h$ 作 sigmod 函数得到逻辑回归假设函数。

• 步骤2：

训练数据集($x^n,\hat y^n$)：当 $\hat y^n$ 为类别1时，取1；为类别2时，取0 。

$L(f)=\frac{1}{2}\sum_n(f_{w,b}(x^n)-\hat y^n)^2$

• 步骤3：

$\frac{\partial (f_{w,b}(x^n)-\hat y)^2}{\partial w_i}$ = $2(f_{w,b}(x^n)-\hat y^n)f_{w,b}(x^n)(1-f_{w,b}(x^n))x_i$

$\hat y^n$ = 0时，

如果 $f_{w,b}(x^n)$ = 1(远离目标)，$\frac{\partial L}{\partial w_i }= 0$

如果 $f_{w,b}(x^n)$ = 0(靠近目标)，$\frac{\partial L}{\partial w_i }= 0$

### **3. 判别模型 v.s. 生成模型 **

3.1 介绍

我们把逻辑回归方法称为判别模型（ Discriminative ）方法，

上节课用高斯方法来描述后验概率的方法称为生成模型（ Generative ）方法。

概率函数 $P_{w,b}(C_1|x)$ ，通过两种不同的方式求解 $w,b$。

• 1 直接求解 $w,b$

• 2 计算 $μ^1$，$μ^2$ ，$\sum^{-1}$ ，再通过下式计算：

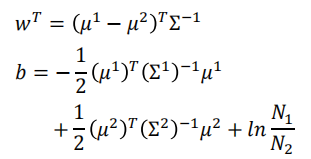
如果使用生成模型，可以使用方法2计算。

它们使用相同的训练数据和函数集进行训练，但是最终的得到的预测函数不相同，如图所示。

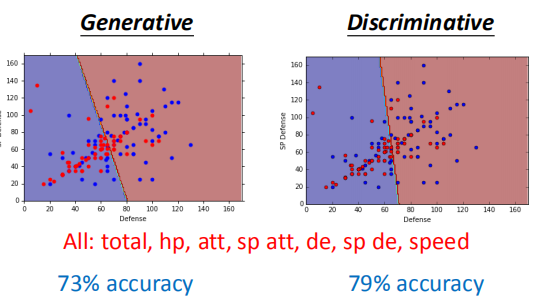上述两种模型采用了数据集的7种数据特征来对数据集进行分类，其中生成模型的准确率为73%，判别模型的准确率为79%。

3.2 生成模型实例

已知特征均为1时，是类别1，其余为类别2。

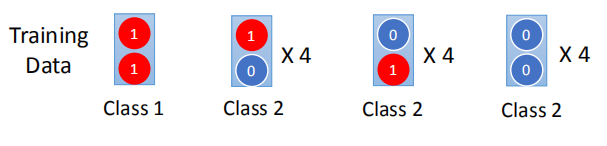我们来预测一下：

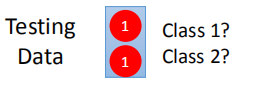如果使用贝叶斯模型（生成模型）会得到什么样的结果？

预测结果为类别2，应该是类别1的，为什么出错了呢？

生成模型经过计算判断测试数据是类别1的几率小于0.5，原因在于生成模型会适当脑补一些情形。

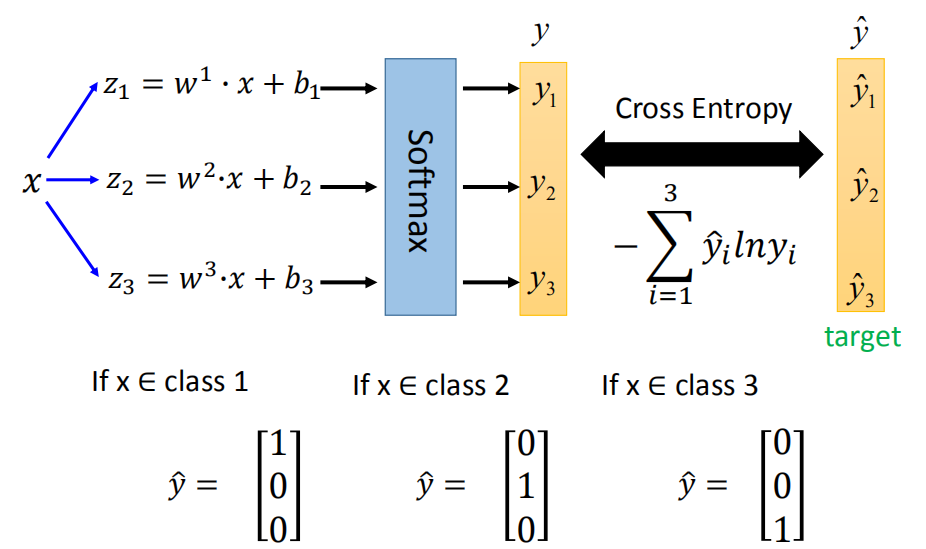
4. 多元分类

类比二元分类，多元分类即根据特征将数据分为多个类别。

$C_1:w^1,b^1$;$z_1 = w^1*x + b_1$

$C_2:w^2,b^2$;$z_2 = w^2*x + b_2$

$C_3:w^3,b^3$;$z_3 = w^3*x + b_3$

Probability：$y_i = P(C_i|x)$

• $1 > y_i >0$

• $\sum_i y_i=1$

使用 softmax 函数：

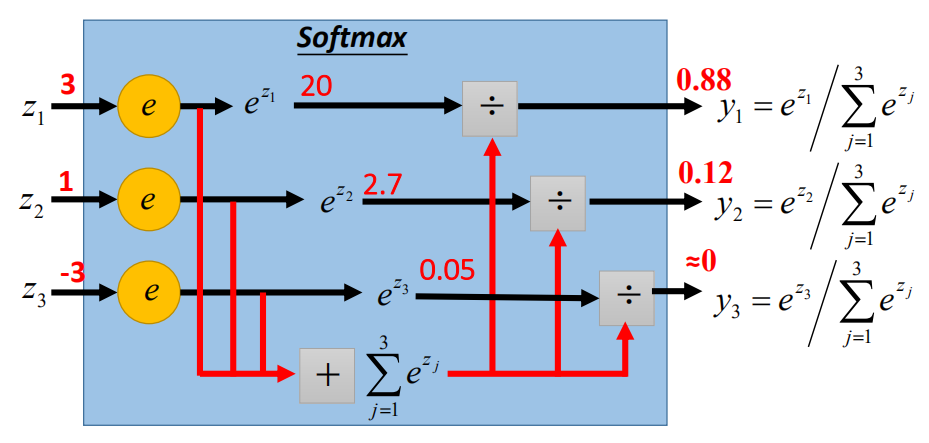
softmax 函数和 交叉熵（ cross entropy ）:

熵的概念本来是热力学的一个概念，描述物质的混乱程度。

在这里，我们用交叉熵的概念来描述两组不同概率数据分布的相似程度，越小越相似。

5. 逻辑回归的局限性

“异或”函数

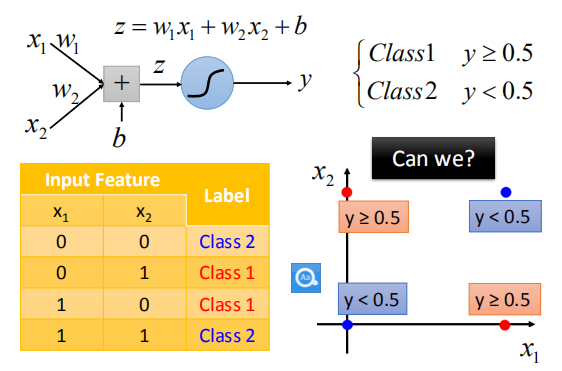
如图，我们不能够将数据集进行很好的分类。请问为什么呢？

解决办法

特征变化：

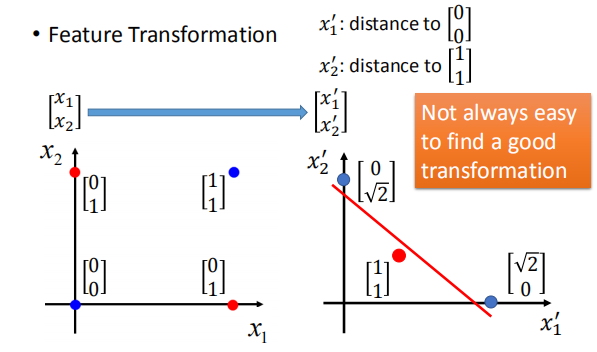如图，我们通过一些变换将数据在坐标轴上分开，但是我们并不能很容易找到一个较好的变换。

级联逻辑回归模型

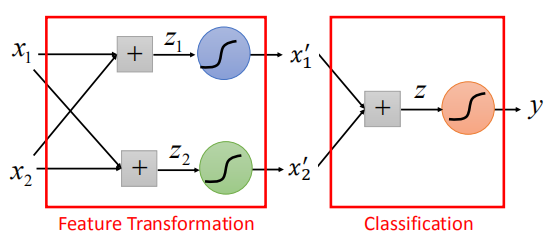
首先通过特征变换，改变每个点的特征值：

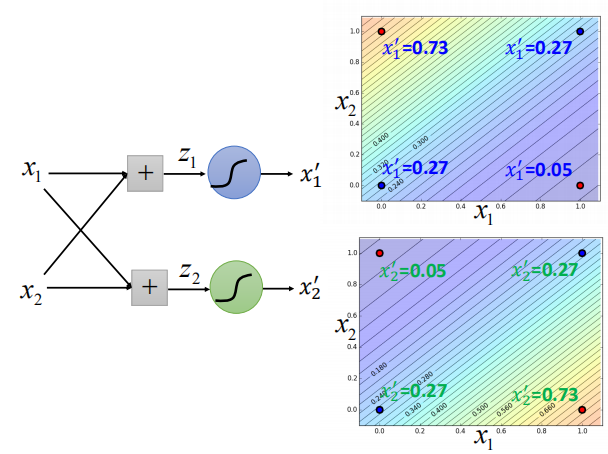
通过第二级模型进行分类：

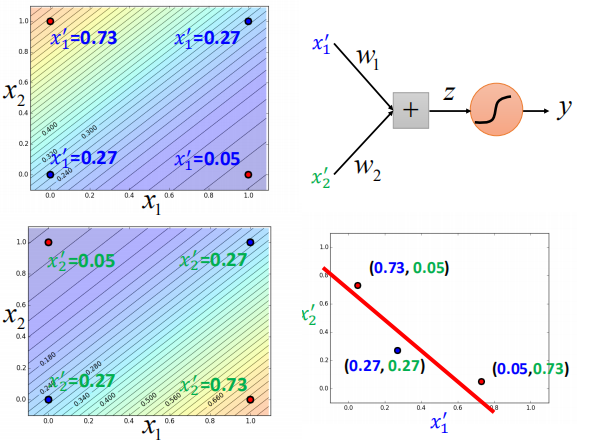
如图，我们成功地将数据进行分类。

6. 深度学习