这一节我们主要学习
- 介绍分类模型
- 利用生成模型求解分类问题
- 利用极大似然估计法求解训练集数据的概率分布
- 通过几率模型,求解生成模型中变量的概率分布
1.分类模型
分类模型:输入一个对象的特征,输出该对象所属的具体类别。
该模型在医疗诊断、人脸识别等问题中有着广泛的应用。
1.1 分类模型的应用
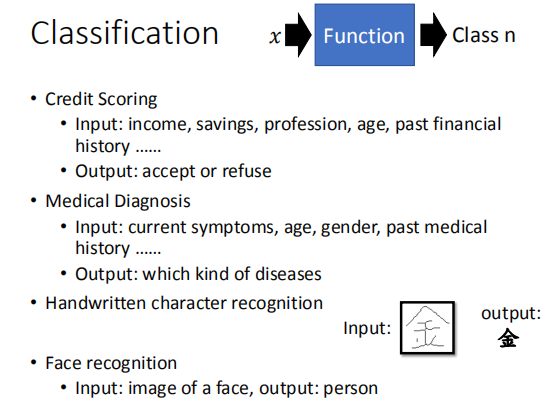
接下以宝可梦的例子作为具体实例来进行分析。
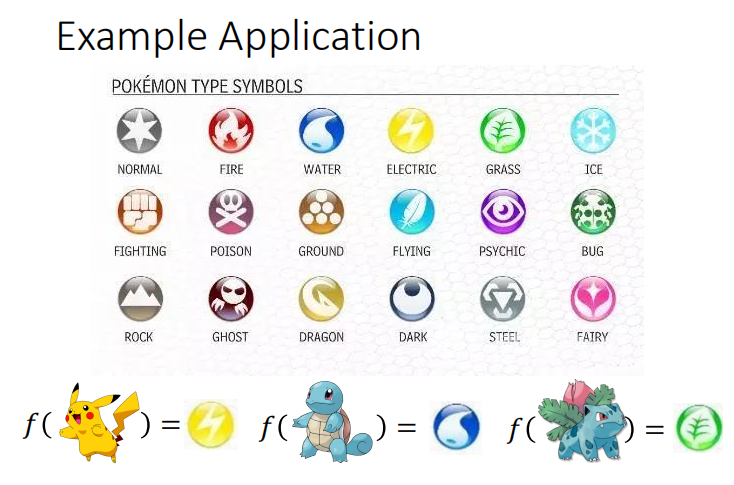
在该实例中,我们将总评分、HP值、攻击力、防御力等参数作为数据特征输入,来预测输出宝可梦的属性,从而进行分类。

1.2 分类流程步骤
- 收集数据进行训练
我们应该将分类问题归类至回归分析中吗?
举个例子,我们首先来看看二分类问题。
在训练集中,我们将类别 1 对应的标签值设为 1 ;类别 2 对应的标签值设为 -1 。
在测试集中,当预测值更接近 1 时,将其归为类别 1 ;更接近 -1 时,归为类别 2 。
这样做会遇到什么问题呢?
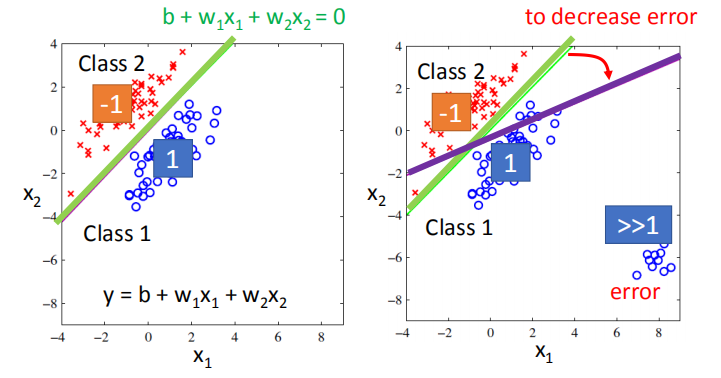
左图中,左上角代表小于 0 ,右下角代表大于 0 ,当特征数据方差较小时,分类良好。
右图中,当特征数据方差较大,比较分散,导致决策边界右下角偏移。
为照顾那些过于“正确”(预测值过大)的样本点,决策边界将会向右下角偏移,从而不能进行正确的分类。
对于多元分类问题,我们将类别 1、2、3…… 的标签值分别置为 1、2、3……
1.3 模型改进
针对上述问题,我们需要找到一个理想的替代函数,来代替线性回归模型。
- 函数(模型):

寻找一个函数 $f(x)$ ,当 $g(x)>0$ 时,输出类别 1 ;否则,输出类别 2。
- 损失函数:
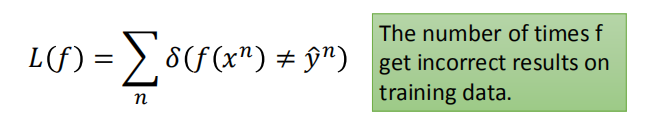
确定损失函数 $L(f)$ ,记录训练中预测错误的次数。
- 确定最佳函数
通过感知神经元、支持向量机等方法,确定最终的最佳函数模型。
2. 分类问题
2.1 盒子问题
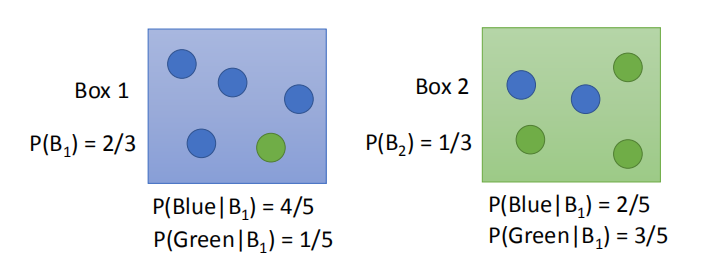
那么问题来了:取出一个球,确定该球的颜色为蓝色,判断该球来自哪个盒子?
(已知取出的球是蓝色的,求来自箱子 1 的概率。)
我们需要用下面公式完成计算:
$P(B_1|Blue)=\frac{P(Blue | B_1)P(B_1)}{P(Blue | B_1)P(B_1)+P(Blue | B_2)P(B_2)}$
上述,是贝叶斯公式。
2.2 二分类问题
推而广之:如果我们看成分类,两个类别如何区分呢?
思路:通过大量的训练集数据,来估测 $P(C_1),P(C_2),P(x | C_1),P(x | C_2)$ 的值 ,再进行正确的分类预测。
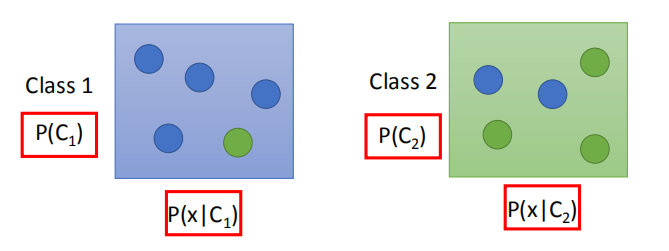
已知一个宝可梦对象的特征变量为 $x$ ,判断宝可梦的类别属性(来自哪个 Class 的概率最大)。
那么给一个 x ,它的分类的概率是:$P(C_1 | x)=\frac{P(x | C_1)P(C_1)}{P(x | C_1)P(C_1)+P(x | C_2)P(C_2)}$
整体 $P(x)$ 的概率是:
生成模型: $P(x)=P(x | C_1)P(C_1)+P(x | C_2)P(C_2)$
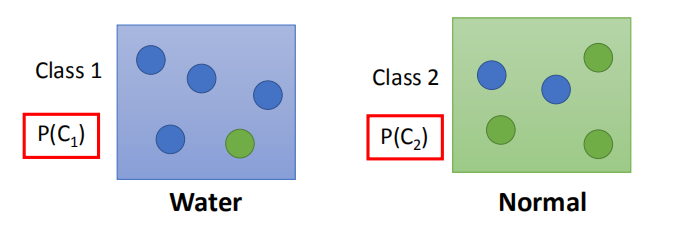
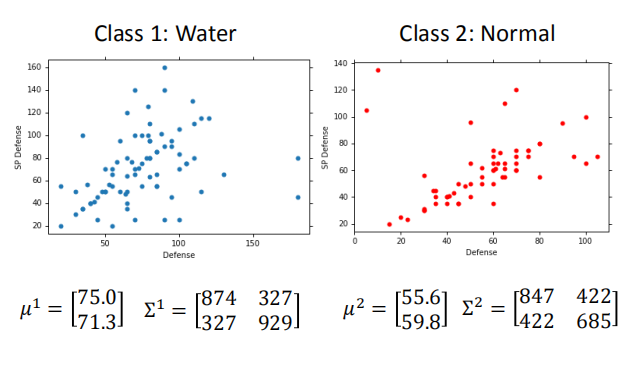
考虑两个类别,Class1 是水系宝可梦,Class2 是普通系宝可梦。
我们将 ID 小于 400 的宝可梦用作训练,剩余的宝可梦用于测试。
其中训练集:水系宝可梦 79 只;普通系宝可梦 61 只。
得到: $P(C_1)=\frac{79}{79+61}$
$P(C_2)=\frac{61}{79+61}$
$P(x | C_1)$ 表示从水系里面挑一只宝可梦,这只宝可梦是 $x$ 的概率值。
每只宝可梦都是用一个向量表示的,它的属性值就是向量里的值。
根据数据特征进行分类:
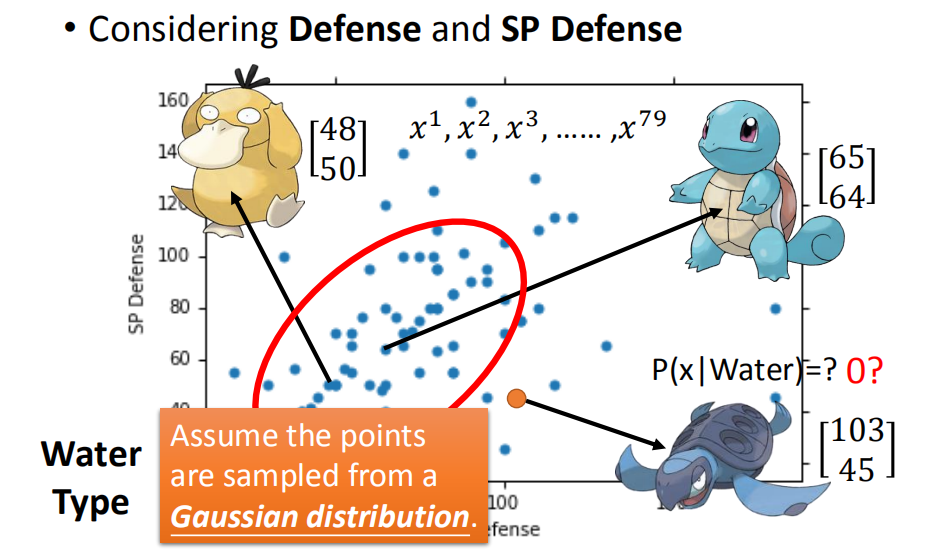
现在取宝可梦的两个属性防御和特殊攻击防御作为一个特征向量。
这样就得到了上图。这个二维平面上每一个点都代表一只宝可梦。
我们假设上面的数据点采样自高斯分布。
3. 最大似然估计
3.1 高斯分布
$f_{μ,\sum}(x)=\frac{1}{(2π)^{D/2}}$ $\frac{1}{|\sum | ^{1/2}}$$\cdot exp{-\frac{1}{2}(x-μ)^T\sum^{-1}(x-μ)}$
输入:样本值 $x$ ;
输出:样本的概率密度。
函数的形状取决于均值 $μ$ 和协方差矩阵 $\sum$
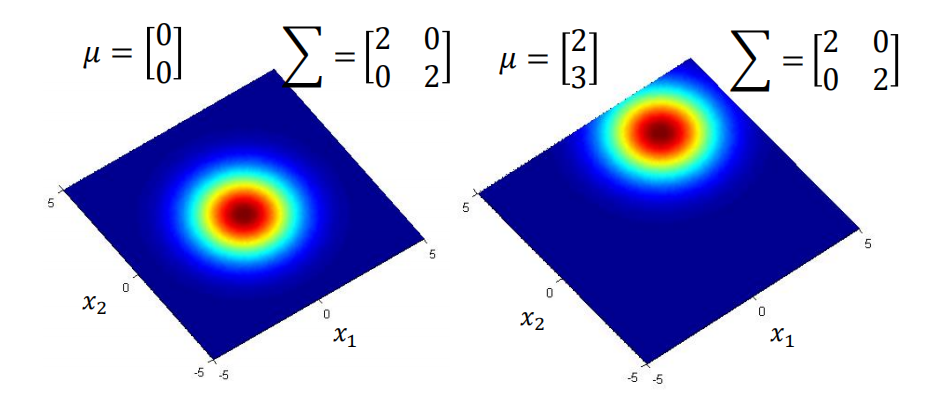
3.2 利用极大似然法求解高斯分布
- 假设这些点采样自高斯分布,我们要通过极大似然估计法找到这个分布,且能够预测新的样本点的概率。
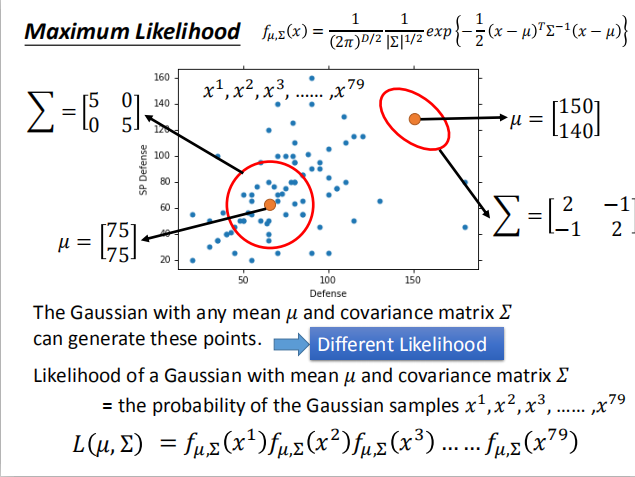
我们拥有水系的宝可梦:$x^1,x^2,x^3,…,x^{79}$,我们假设这些样本点均来自高斯分布 $(μ,\sum)$ ,使得最大似然函数 $L(\mu,\sum)$ 最大。
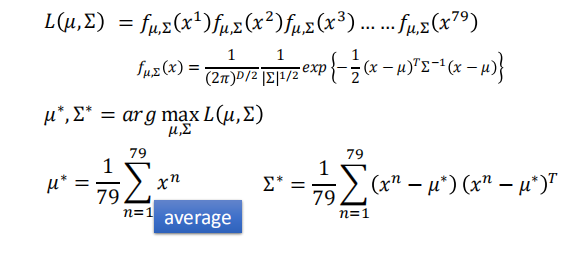
- 通过上述公式,我们可以求出水系和普通系宝可梦的高斯分布。
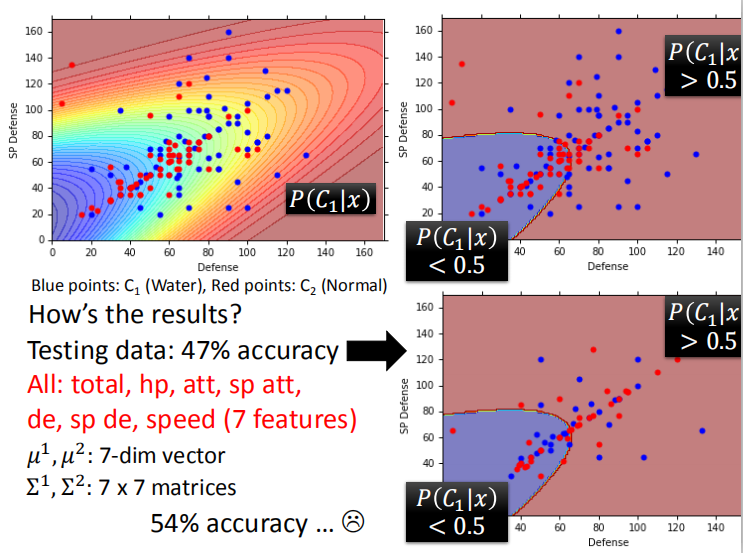
3.3 分类预测
- 通过生成模型,我们可以对新的样本点进行预测分类。

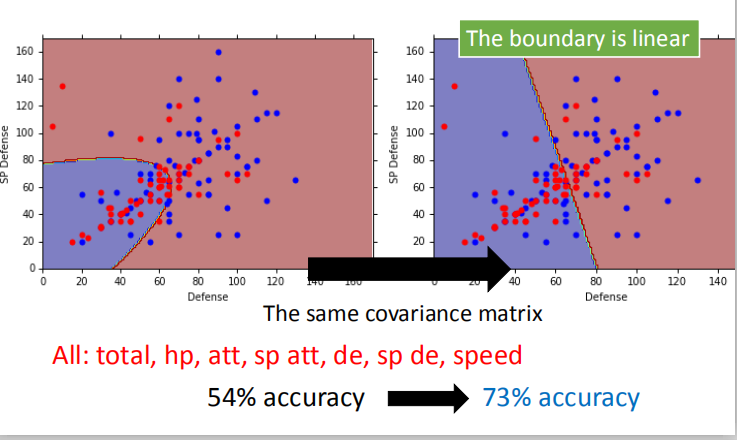
- 模型的预测结果:该模型的准确率仅仅为 54% ,效果不是特别理想。
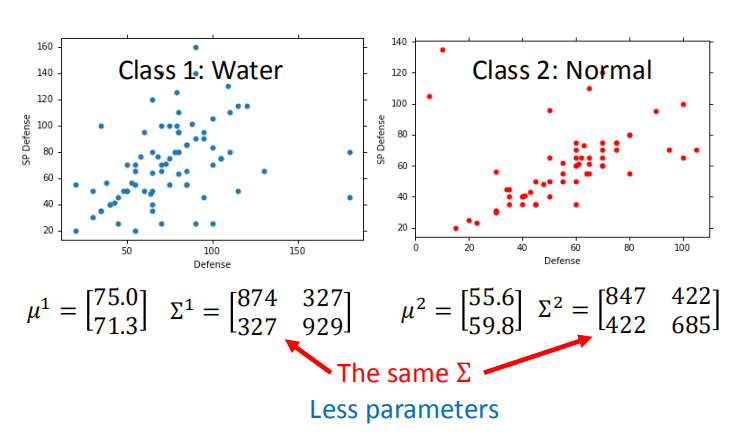
3.4 模型改进
- 针对两个属性的不同高斯分布,将两个分布的协方差矩阵设为相同的值,减少参数的数量,避免过拟合。
- 使用最大似然估计法求解:

- 改良后的模型:准确率由之前的 54% 提升至 73%
4.几率模型
4.1 几率模型的三个步骤
- 寻找函数集(模型)
- 评价模型的好坏
- 确定最终的模型

4.2 概率分布
- 按照自己的意愿选择数据的概率分布

如果你假设 $x$ 各个维度是相互独立的,那么你正在使用朴素贝叶斯分类器。
但是这样的模型有时可能过于简单,效果不是特别好;需要在各个特征之间添加一些联系,使模型更加复杂。
并不是所有的模型都是高斯分布。对于一些二分类问题,你可以假设它们来自伯努利分布来生成概率模型,然后进行分类预测。
#### 4.3 后验概率
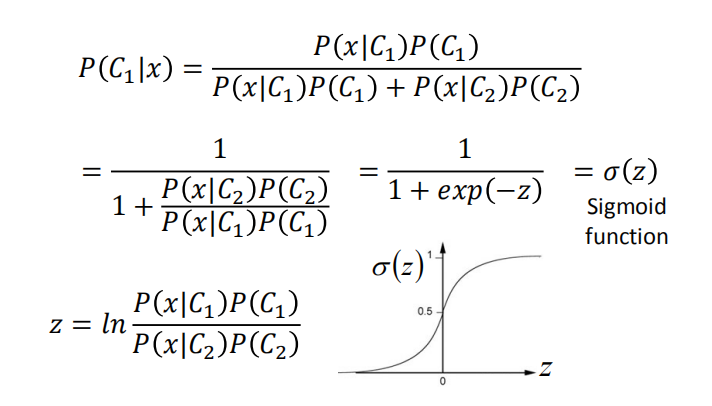
通过代数变换,我们将分类预测变成关于$z$ 的 $sigmoid$ 函数,其中 $P(x|C_1),P(x|C_2)$ 满足高斯分布。

- 我们将 $P(x|C_1),P(x|C_2)$和 $P(C_1),P(C_2)$的表达式带入化简得到 $z$ 的新的表达式:

- 当两个高斯分布的协方差相同时,即 $\sum^1 = \sum^2$,进一步简化 $z$ 的表达式:

在生成模型中,我们通过训练集数据,估计$N_1,N_2,μ^1,μ^2,\sum$ .