这节我们主要学习

• 误差的来源
• 偏差
• 方差
• 过拟合、欠拟合与误差的关系
• 交叉验证

1. 误差的来源

通过上一节课的学习，我们知道：

• 选择不同的函数集就是选择不同的模型，在训练集和测试集上得到不同的误差 (error)。
• 越复杂的模型不一定误差最小。

那么我们现在讨论误差的来源：

• bias 偏差
• variance 方差

如果知道误差的来源，就可以采用适当的方法来优化模型。

2. 误差来源的实例分析

上一节课中，我们需要估测宝可梦进化后CP值。

我们需要找到一个函数，能够准确预测每一个宝可梦进化后的 CP 值。

理论上，有一个最佳的函数，我们记作：$\widehat{y}=\widehat{f}(宝可梦)$

实际上我们是不知道最佳模型的。

我们根据训练集数据找到最好的模型，记作：$f^*$（$f^*$ 是 $\widehat{f}$ 的估测值）

它们俩之间的距离大小来自 2 个方面：可能来源于偏差，也可能来源于方差。

那么一个评价模型的偏差和方差指的是什么呢？

3. 理解方差和偏差

• 估计变量 $X$ 的期望

  • 假设 $x$ 的平均值是 $\mu$
  • 假设 $x$ 的方差是 $\sigma^2$

• 均值 $\mu$ 的估计量

  • 简单取样 $N$ 个样本点：{$x^1,x^2,…,x^N$}
  • 计算 $N$ 个点的平均值和方差 $s^2$：

  $m={\frac{1}{N}\sum_n{x^n}}$

  $s^2 = \frac{1}{N}\sum_{n}(x^n-m)^2$

  • 将以上试验多次，然后计算 $m$ 的平均值:

  $E[m] = E[\frac{1}{N}\sum_n{x^n}]=\frac{1}{N}\sum_{n}{E[x^n]}=\mu$

  $Var[m]=\frac{\sigma^2}{N}$

  偏差估计值：

  $E[s^2]=\frac{N-1}{N}\sigma^2 \neq \sigma^2$

  m 分散在 $\mu$ 周围，分散的情形取决于 m 的方差，而方差的大小取决于 $N$。

【注意】：视频中的 Larger N 和 Smaller N 放反了。

4. 方差和偏差的几种情况

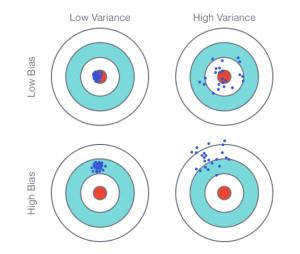
我们要估测的是靶的中心，这个是我们的目标。

通过许多次试验，我们发现你其中一个射中的位置，记作 $f^*$，

它与靶心中心 $\widehat{f}$ 之间的距离，其实是发生了两件事，即等价于他们之间的误差取决于两件事：

• 第一件事情就是：你瞄准的位置在哪里？

  换句话说就是你瞄准位置的期望与靶心之间的偏差，计算如下：

  $f^* $ 的平均值：$E[f^*]=\overline{f} $，

  即：你没有瞄准靶心，你以为你瞄准的靶心与实际的靶心是有偏差 (bias)

• 第二件事情就是：

  你瞄准的靶心 $E[f^*]=\overline{f}$ 与射中的位置 $f^*$ 是有偏移的。

  所以每次的 $f^*$ 是不一样的，

  而每一次的 $f^*$ 与 $E[f^*]=\overline{f}$ 之间的距离就是方差 (variance)

所以误差大小取决于偏置和方差的大小。

我们期待的是没有偏差（Low Bias），而且方差较小（Low Variance）。

但是有时我们得到的有时方差很小，但是偏离靶心比较远，此时是 High Bias 和 Low Variance，

又或者我们得到是目标是分散在靶心周围，这样也会得到一些误差。

多次试验宝可梦模型理解方差和偏差

在不同的平行宇宙抓到 10 只宝可梦来计算不同的 $f^*$，

在不同的宇宙中抓到的宝可梦是不一样的：

• 第一个宇宙中的我，抓到 10 只宝可梦；

• 第二个宇宙中的我(衣服颜色与第一个不同)，抓到另外 10 只宝可梦；

• 第三个宇宙中的我(性别已经换掉),抓到的是其他 10 只宝可梦；

每一次抓到的宝可梦是不一样的。

如果你拿不同的宝可梦来找到你最好的 function，就算你用同一个模型，得到的结果也会不同。

假设我们现在都用 $y=b+w \cdot x_{cp}$ 这个模型，

但是你给他输入的 data 不一样，最后得到的 $f^*$ 就不一样。

我们在 100 个平行宇宙中分别抓取 10 个宝可梦，每个平行宇宙中都用 $y=b+w \cdot x_{cp}$ 模型，

可以得到不同的 $f^*$ 的分布情况，然后将得到 100 个不同 $w$ 和 $b$，将每一条直线都绘制出来，最后得到的结果如图：

如果采用不同的 model 呢？

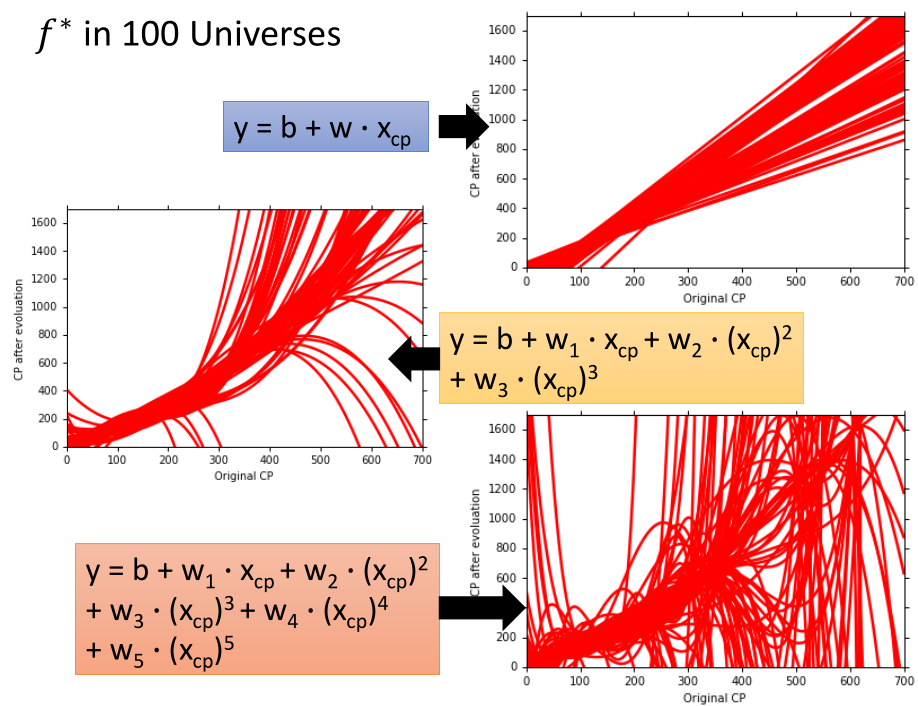
• 方差

如果全部采用直线模型，得到的方差就比较小。

如果用比较复杂的模型，误差点散的比较开，方差就比较大，而且各种曲线长得都不像。

• 偏差

偏差：我们有很多 $f^*$，找到它们的期望值 $E[f^*]=\overline{f}$，描述 $\overline{f}$ 与 $\widehat{f}$ 接近程度。

如果偏差比较大，说明 $\overline{f}$ 与靶心 $\widehat{f}$ 距离较大；

如果偏差比较小，说明 $\overline{f}$ 与靶心 $\widehat{f}$ 距离较小；

实际测量时，无法清晰的获取 $\widehat{f}$ 的位置，故假设一条曲线作为 $\widehat{f}$，

宝可梦依次 $\widehat{f}$ 曲线上取样 10 个点，然后求取 $\overline{f}$。

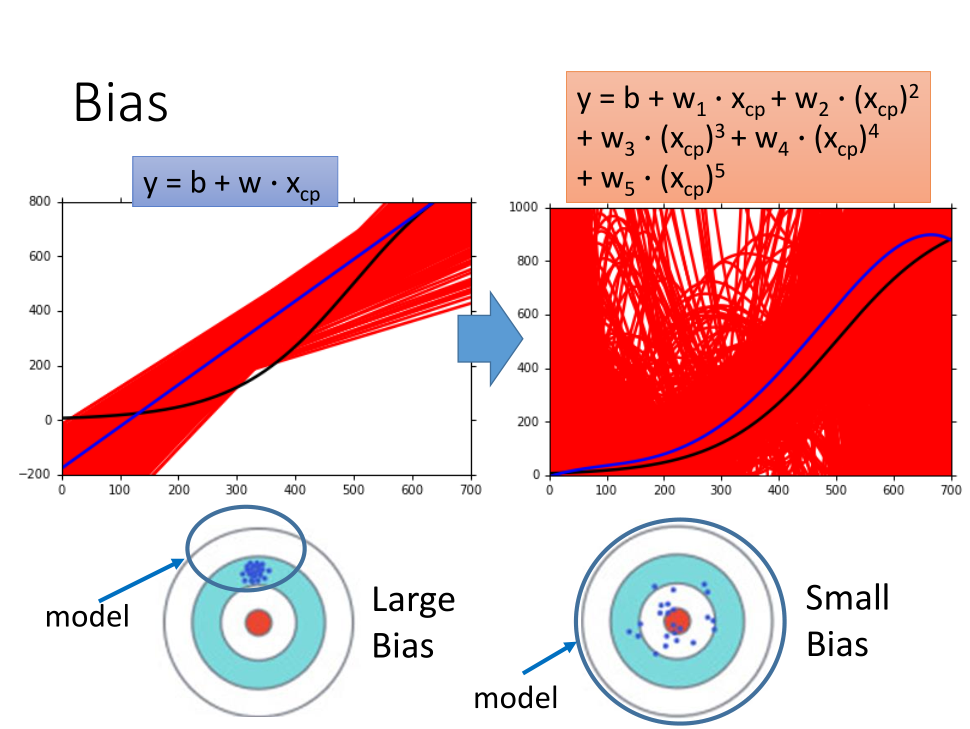
试验结果：

• 黑色曲线：真实的靶心位置 $\widehat{f}$

• 红色部分：表示我们做 5000 次试验得到的 $f^*$

• 蓝色曲线：表示 5000 次试验 $f^*$ 的平均值 $\overline{f}$

然后分别用三次式和五次式进行试验，发现五次式中每一个差距很大，但是平均后的蓝线和实际中心黑线很接近。

总结：

• 简单模型得到的偏差比较大，方差较小。

• 复杂模型得到的偏差比较小，方差较大。

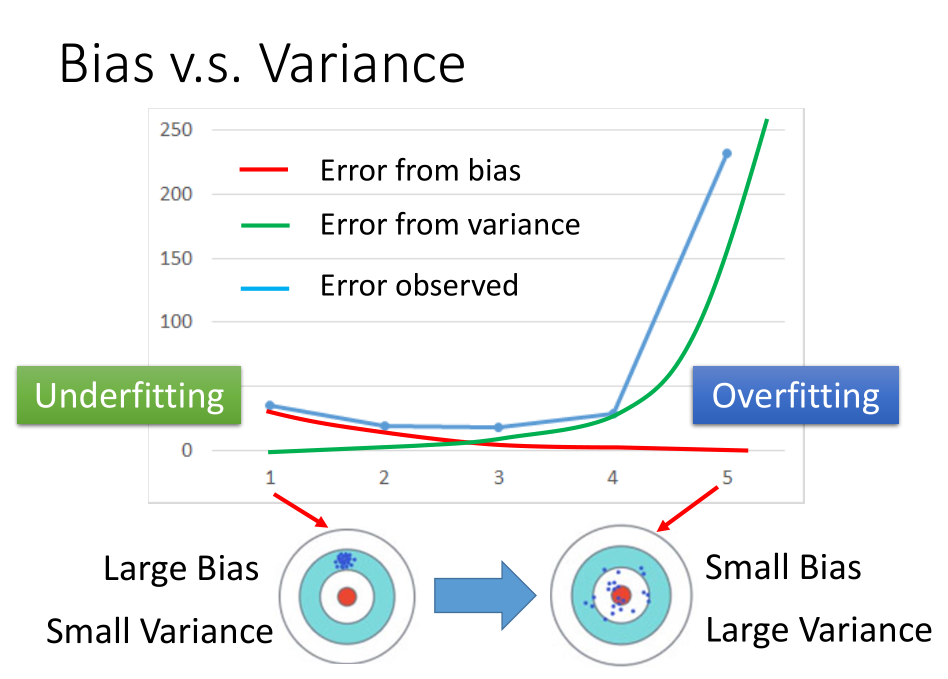
5. 欠拟合和过拟合与误差之间的关系

• 如何知道遇到的问题是偏差较大还是方差较大呢？

如果模型不能够拟合训练集，则是偏差比较大，此时是欠拟合，

如果模型能够很好的拟合数据，但是在测试集上有较大的误差，此时模型可能有较大的方差，此时是过拟合。

• 欠拟合解决方式：
  • 添加更多的特征
  • 选择更复杂的模型
• 过拟合解决方式：
  • 增加数据(非常有效但有点不实际)
  • 正则化
• 模型选择注意事项：
  • 在方差和偏差之间找到平衡
  • 选择一个能够使得偏差和方差综合误差最小的模型
  • 不能够做的：

不能够根据 private testing set 的误差来选择模型，要考虑 public testing set，故可以采用交叉验证来解决这个问题。

6. 交叉验证

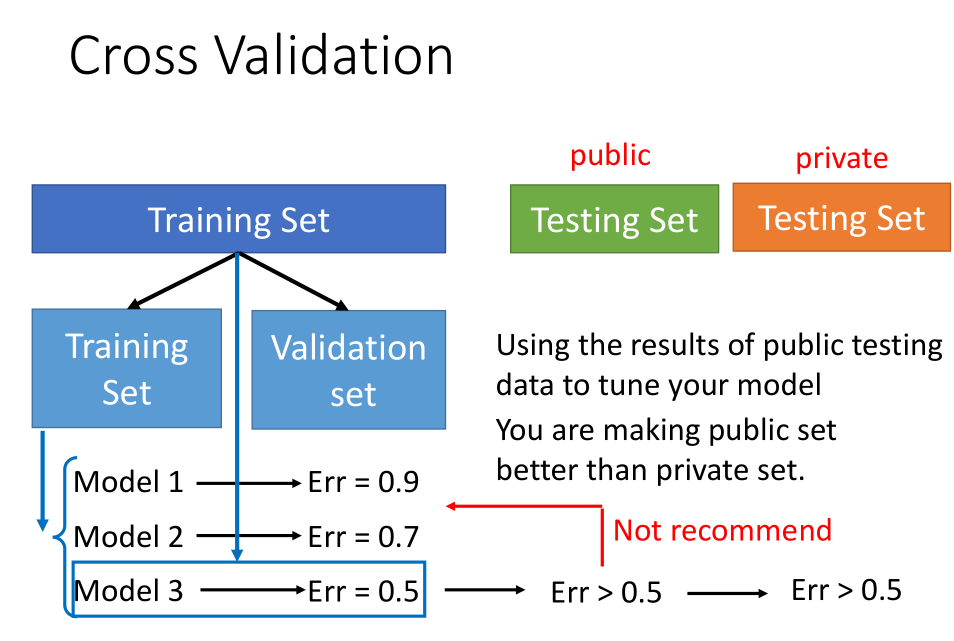一般数据集分为训练集和测试集，将训练集分为训练集和验证集，然后根据验证集上的误差选择模型，

从而来得到测试集上的误差。

一般测试集上的误差大于验证集上的误差。

不要因为测试上的误差大于验证集上的误差而在模型上做工作，此时相当于把测试集上的偏差考虑进去。

• n-折交叉验证

  

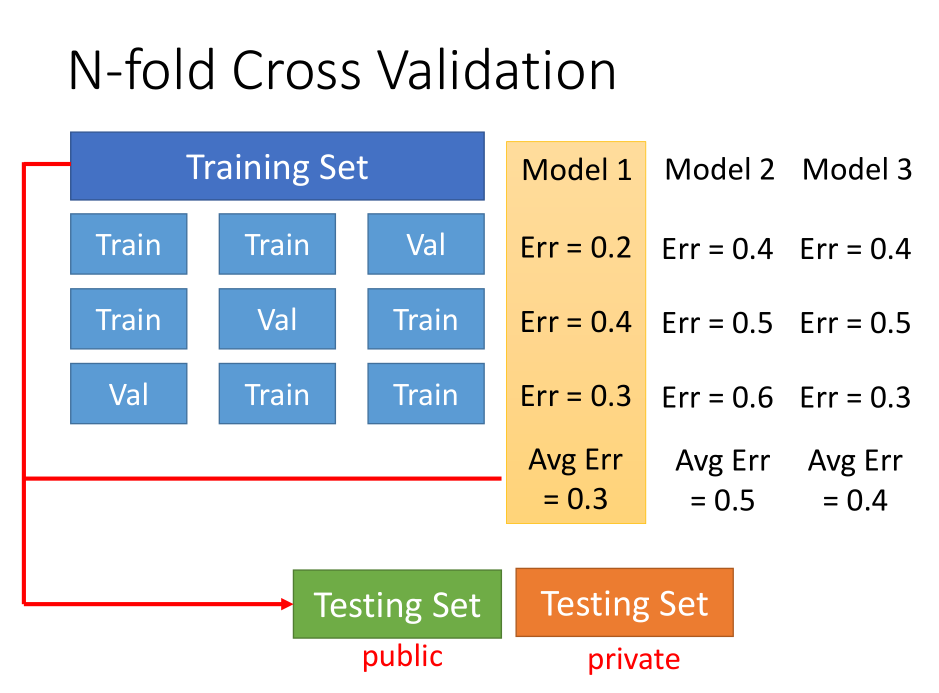
图示是 3-折交叉验证，即将训练集分成 3 份，每一次拿其中 1 份作为验证集，另外 2 份作为训练集。

然后每一次分别得到模型的误差，每一个模型对应的训练 3 次，然后得到每一个模型的平均误差。

选择平均误差最小的那个模型即可，然后将选择的模型在训练集上跑一遍后在测试集上使用。