这一节我们主要学习
- 生成模型中的半监督学习（Semi-supervised Learning for Generative Model）
- 低密度分离（Low-density Separation）
- 平滑性假设（Smoothness Assumption）
- 更好的表达（Better Representation）
1.半监督学习介绍
- 监督学习：${x^r,\hat{y}^r}_{r=1}^{R}$
- $x^r：$输入特征，比如 image
- $\hat{y}^r：$类别标签
- 半监督学习：${x^r,\hat{y}^r}_{r=1}^{R}，{x^u}_{u=R}^{R+U}$
- 没有标签的数据远大于有标签的数据，即 $U \gg R$
- 转化学习（Transductive learning）：无标签的数据是测试集数据（除去label）
- 归纳学习（Inductive learning）：无标签的数据不包括测试数据
- 为什么做半监督学习？
- 数据的收集比较容易，但是得到有标签的数据是比较麻烦的；
- 人类本身的学习过程就是一种半监督学习。
- 在进行半监督学习的过程中，我们需要作出一些假设，而半监督学习能否取得理想中的效果取决于我们作出的假设是否精确、是否符合实际。
如上图所示，当未加入无标签的数据的时候，我们画出的决策边界是竖着的那条红线；
当我们加入一些无标签的数据（灰色的数据点）之后，我们得到的边界可能会变成斜着的那条线。
因为当给出那些无标签的数据点的时候，我们会假设左下角的数据点是猫，从而得出新的决策边界。
但是我们作出的假设不一定正确，因此假设的合理性很大程度上决定了半监督学习的有效性。
2. 半监督学习生成模型
- 监督学习生成模型训练流程：
- 带标签的训练样本$x^r \in C_1,C_2$
- 计算先验概率分布$P（C_i）$和条件概率分布$P(x|C_i)$
- 条件概率分布符合均值$\mu^i$、方差$\Sigma$的高斯分布
- 根据贝叶斯公式计算后验概率$P（C_i|x）$，将后验概率最大的类作为$x$的输出类
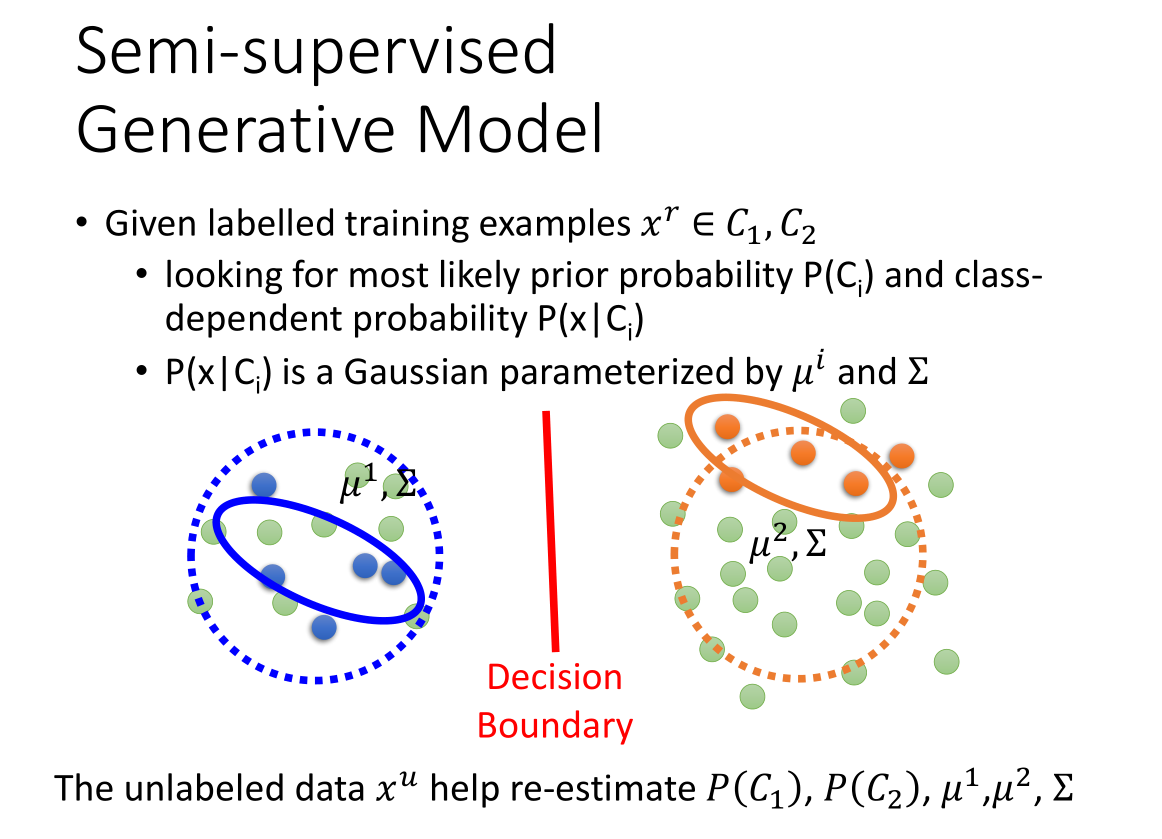
上图中，红色的点和蓝色的点代表有标签的数据，绿色的点代表无标签数据。
加入无标签的数据点之后，数据点的分布发生了改变：由实线表示的分布变成虚线表示的分布。
无标签数据$x^{\mu}$ 对先验概率分布$P（C_i）$、条件概率分布$P(x|C_i)$、高斯分布参数$\mu^i,\sum$估测有影响，从而影响决策边界。
- 初始化参数：$\theta={P(C_i),u^i,\sum}$
- step1：计算无标签数据$P_{\theta}(C_i|x^{\mu})$,依赖模型参数
- step2：按照图中表达式更新模型
- 将更新后的模型进行第一步操作，重新计算$P_{\theta}(C_i|x^{\mu})$,然后继续更新模型，依此迭代…
理论上该方法会收敛，初始值影响收敛的结果。
在监督学习生成模型中，我们需要最大化的似然函数为 $logL(\theta)=\sum_{x^r}P_{\theta}(x^r,\hat y^r)$。
在半监督学习生成模型中，我们除了需要考虑有标签数据之外，还要考虑无标签数据产生的概率 $P_{\theta}(x^u)$，
最大似然函数变为$logL(\theta)=\sum_{x^r}P_{\theta}(x^r,\hat y^r)+\sum_{x^u}P_{\theta}(x^u)$。
由于加入无标签数据后，似然函数不再是凸函数，最终的取值与初始化参数 $\theta$ 有关；
我们需要在每次更新参数 $\theta$ 之后，求解一次似然函数的最大值。（EM算法）
3.半监督学习低密度分离
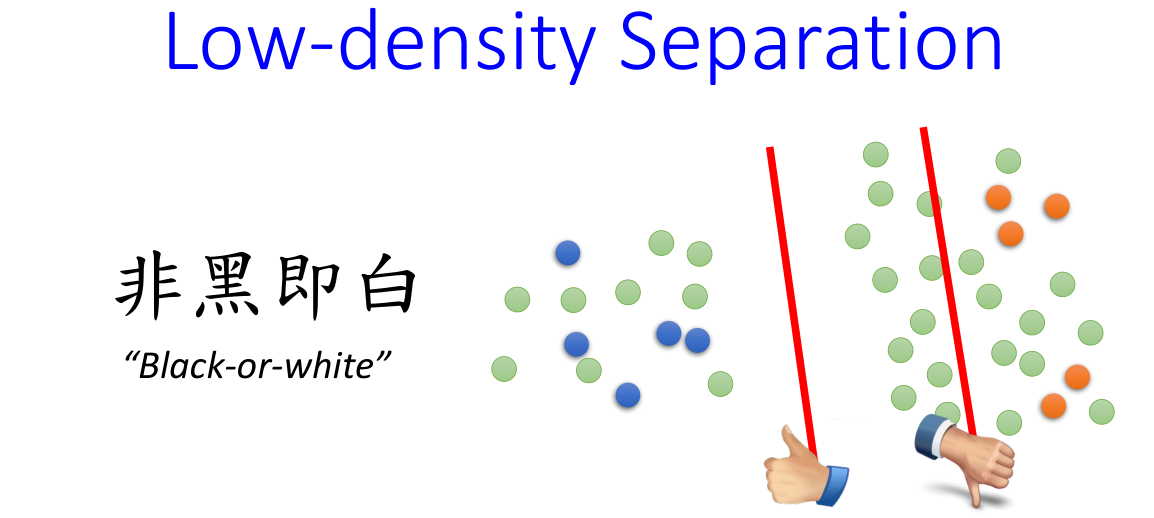相比于之前的生成模型，这里我们作出一个假设：
如果一个数据样本不属于类别一，那么它一定属于类别二。
我们将这种做法产生的标签称为硬标签。
- 数据集：
- 有标签数据集${(x^r,\hat{y}^r)}_{r=1}^R$
- 无标签数据集${x^u}_{u=l}^{R+U}$
- 循环：
- step1:用已知标签的数据训练（利用逻辑回归，神经网络，决策树等方法）出模型 $f^*$
- step2:将未知标签的数据带入该函数中，得到“新标签”。
- step3:然后从得到“新标签”的未知标签的数据中抽取一些数据放入已知标签的数据中。
- 重复上述步骤。
补充：
我们可以通过给未知标签的数据添加权重的方式来辅助抽取数据；对于回归函数而言，这种训练方式对函数没有影响。
我们可以通过熵来度量通过函数 f 给未知标签的数据生成的标签的质量。熵越小，表示生成的标签质量越高。
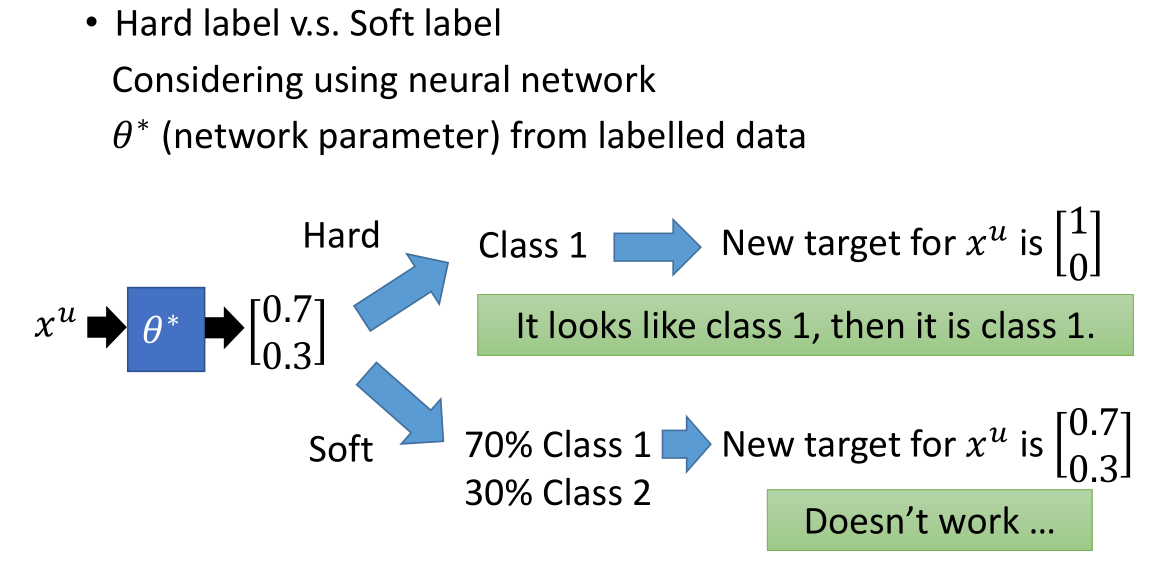自我学习的方法与生成模型有些类似，但是前者采用的是硬标签，后者采用的是软标签。
在神经网络中，假设模型预测某一个样本是类别一的概率为 0.7，是类别二的概率为 0.3。
若采取硬标签的方法，我们会将该样本的标签值设为 [1 0]；
若采取软标签的方法，则标签值依旧为 [0.7 0.3]。
对于神经网络而言，当我们采用硬标签时，才会对模型产生影响。
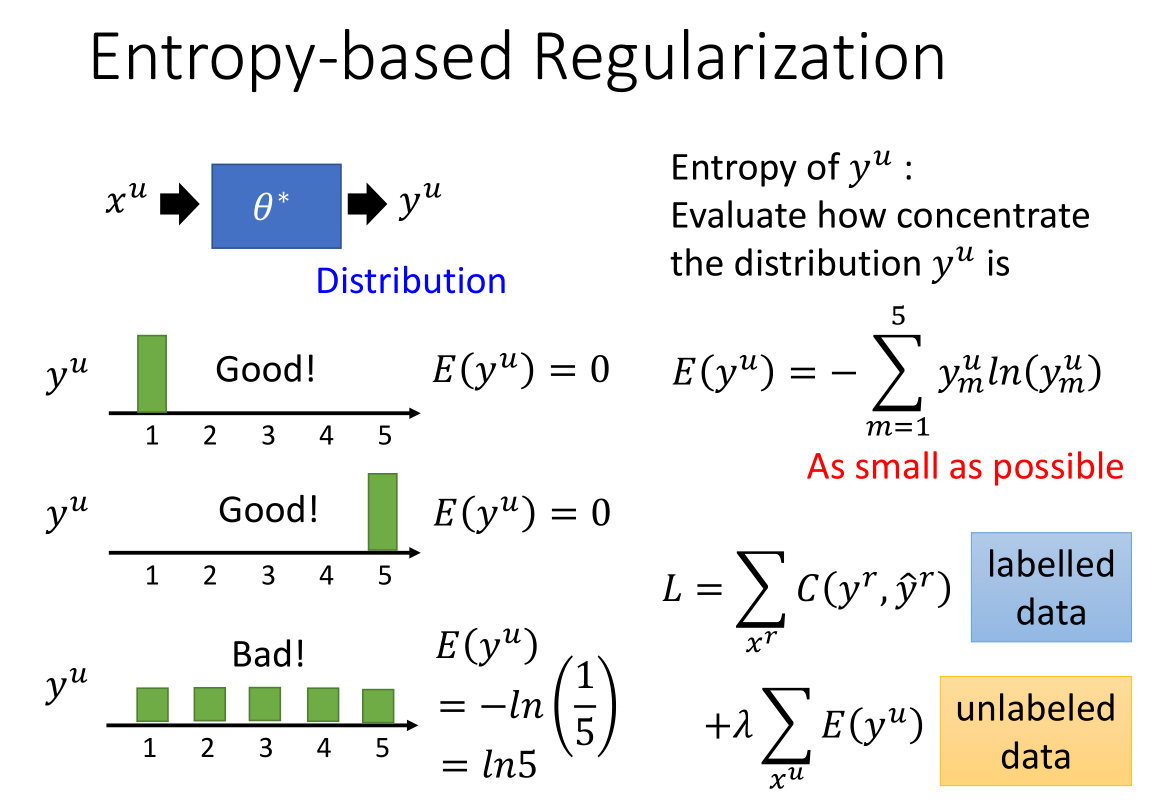
我们依据训练好的模型参数来得到无标签数据的概率分布，
我们希望无标签数据的预测值越集中越好。如左下 3 个预测值中前两个比较密集集；第三个就比较平均，ji不是令人十分满意。
我们引入熵的公式，来评估数据的分布是否集中。
如图所示，前两个的熵是 0，第三个的熵最大是ln5。熵越小说明数据的分布越集中，预测的结果越好。
我们在损失函数上加了无标签部分的熵的正则项，$\lambda$ 来决定是考虑有标签数据多一点还是考虑无标签数据多一点。
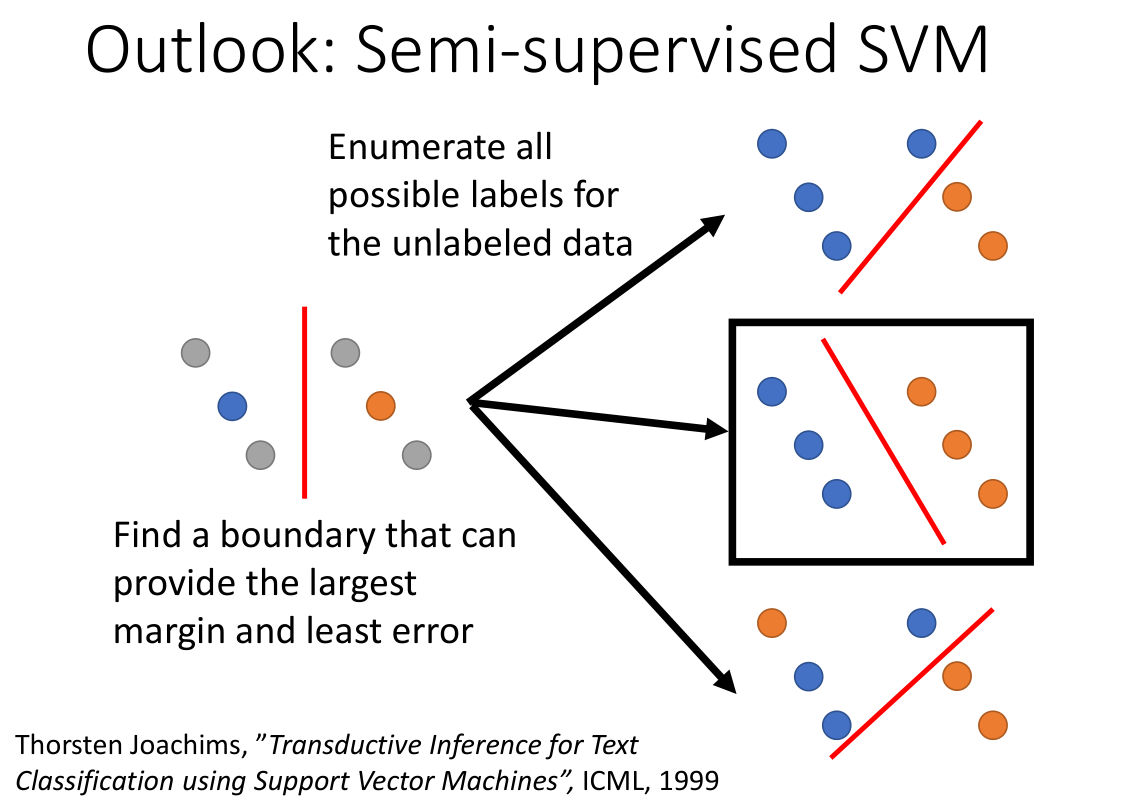
如上图所示，假设我们有 4 个未标记的数据，支持向量机会找到一个最大间隔并使误差最小的边界。
这里对无标签数据集采用枚举法遍历其所有的可能性。然后分别作出每种可能性的决策边界，并从中选出分类边距最大的那个（图中黑色方框）。
假如我们有 M 个未标签数据，则需要做 $2^M$ 个假设。
但是在实际操作中，我们都是改变一笔数据的标签观察边界是否变大，如果变大就采用该假设。
4 平滑假设
4.1 平滑假设的方法介绍
平滑性假设的主要思想是“近朱者赤,近墨者黑”，我们将具有相似性的数据样本归为同一类。
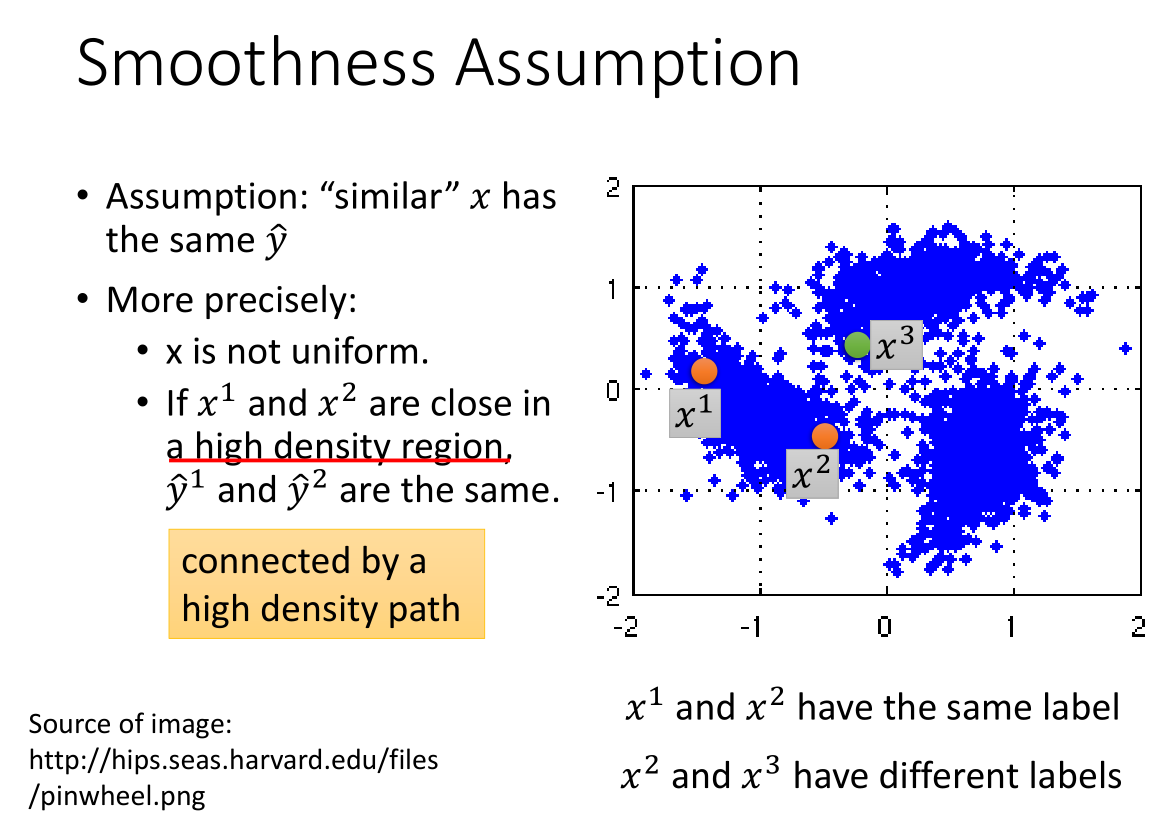
假设 x 分布是不均匀的，某些地方很集中而某些地方很分散；
如果 $x^1$ 和 $x^2$ 分布在一个很集中区域，那么它们对应的标签 $\hat{y}^1$ 和 $\hat{y}^2$ 是相等的。
比如图中 $x^1$ 和 $x^2$ 相近且在一个高密度的区域中，则它们的标签相同；
仅仅观察 x 特征似乎 $x^2$ 和 $x^3$ 比较相近，但是实际上 $x^1$ 和 $x^2$ 在一簇里，而 $x^3$ 在另外一簇。
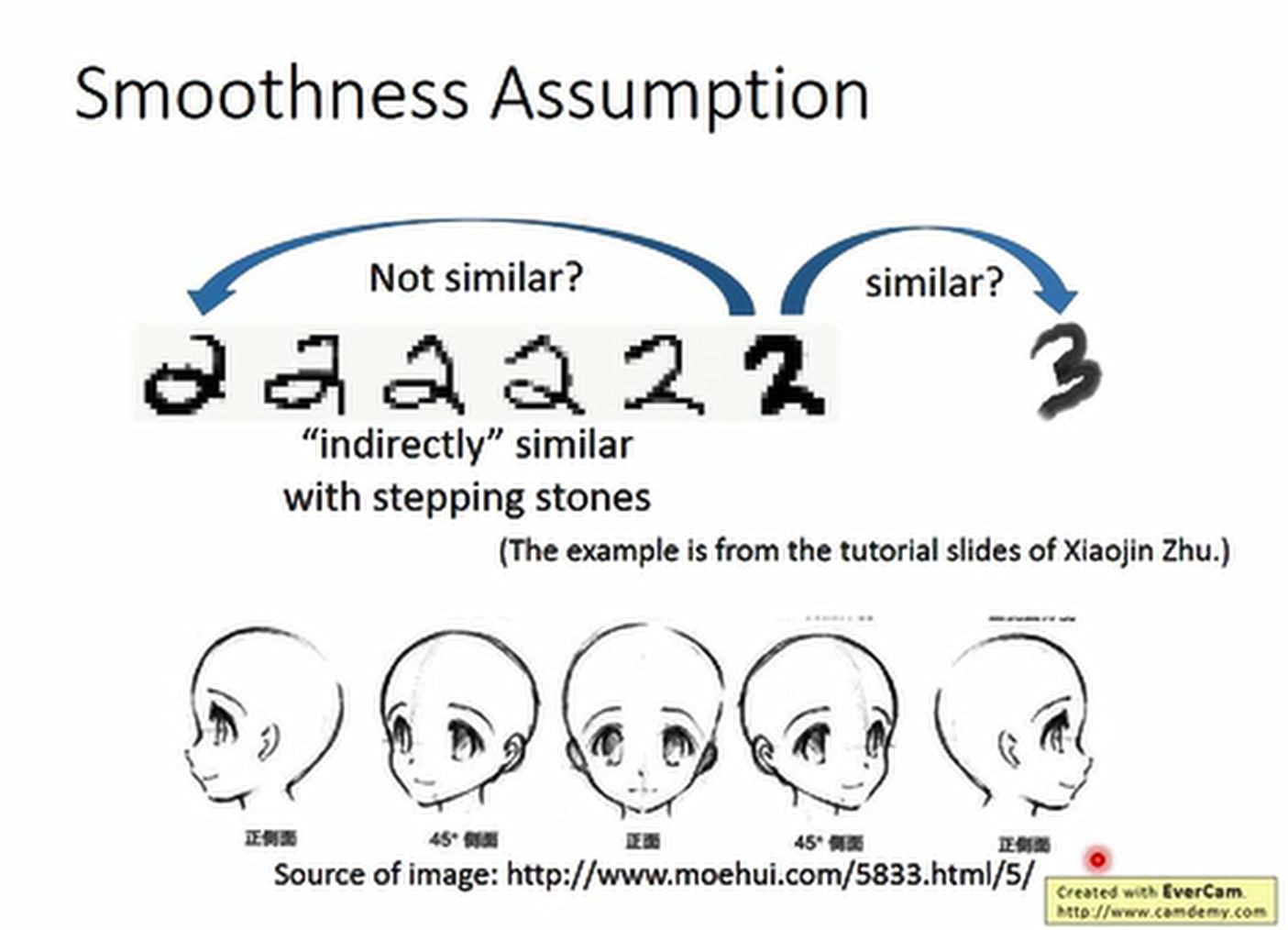比如我们手写数字，两个 2，一个带一个包围的弯，一个没有，可能后边的 2 反而和 3 比较像。
但是看大部分没标签的数据，我们会发现这两个 2 其实是通过很多个过渡的 2 连接在一起，
但是 2 和 3 虽然比之前的2接近，但是他们之间并没有过渡的数据。
比如左侧人脸和右侧人脸，从图片数据上可能另一个左侧人脸和图片左侧人脸都比较接近，
但是当引入过渡数据（不同角度的人脸后）就会发现其实他们是1类。
4.2 平滑假设的实现方法
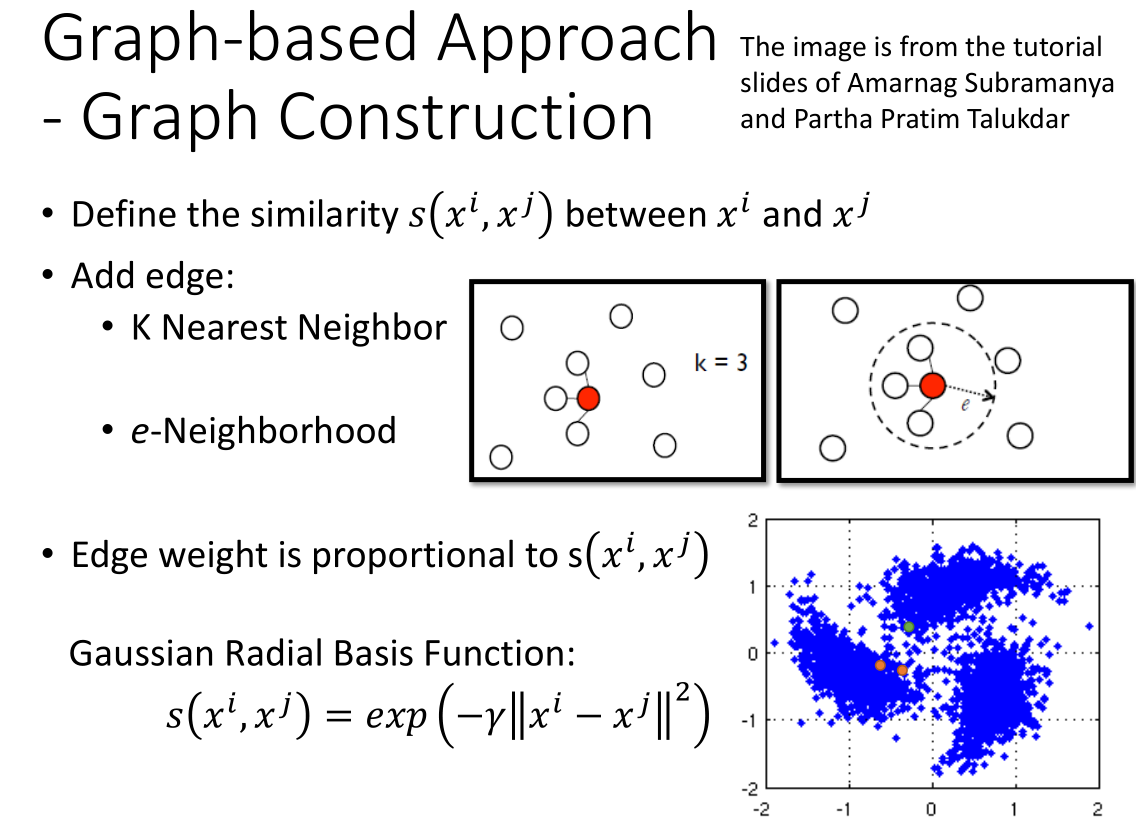
- 计算两个数据点之间的相似度
- 根据计算出的相似度，利用 KNN 算法或者 e-neighborhood(e-邻居算法)给数据点之间加边
- 我们还可以给每条边增加权重，这里我们采用高斯径向基函数来计算相似度作为权重。采用高斯径向基函数有一个好处
就是对于那些距离不是特别近的点，权重会非常小，有利于聚类。
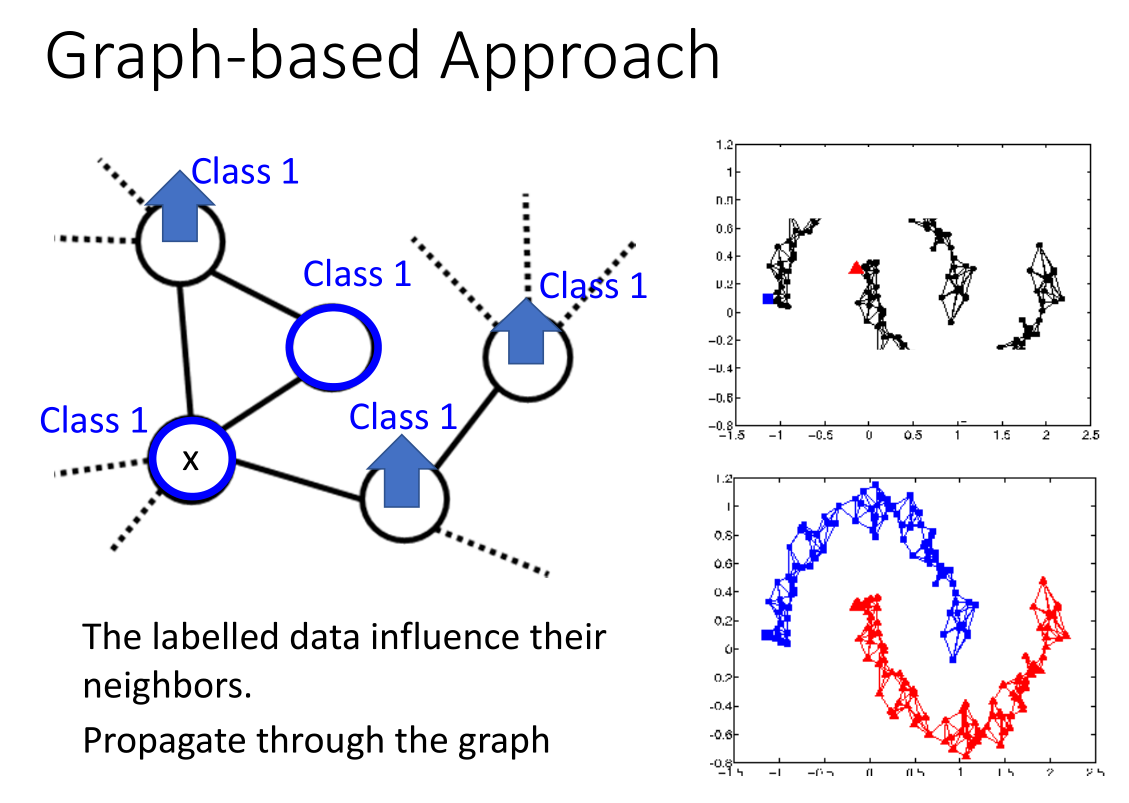基于图的方法的好处是可以将标签传递出去，当然这样的做法就需要海量的数据，否则这种连接就可能断掉。
带标签的数据通过图来影响与其相邻的点。
图中不同数据点的标签之间的平滑度的定义如下：
$S=\frac{1}{2}\sum_{i,j} w_{i,j}{(y^i-y^j)}^2$
我们希望平滑度 S 越小越好。
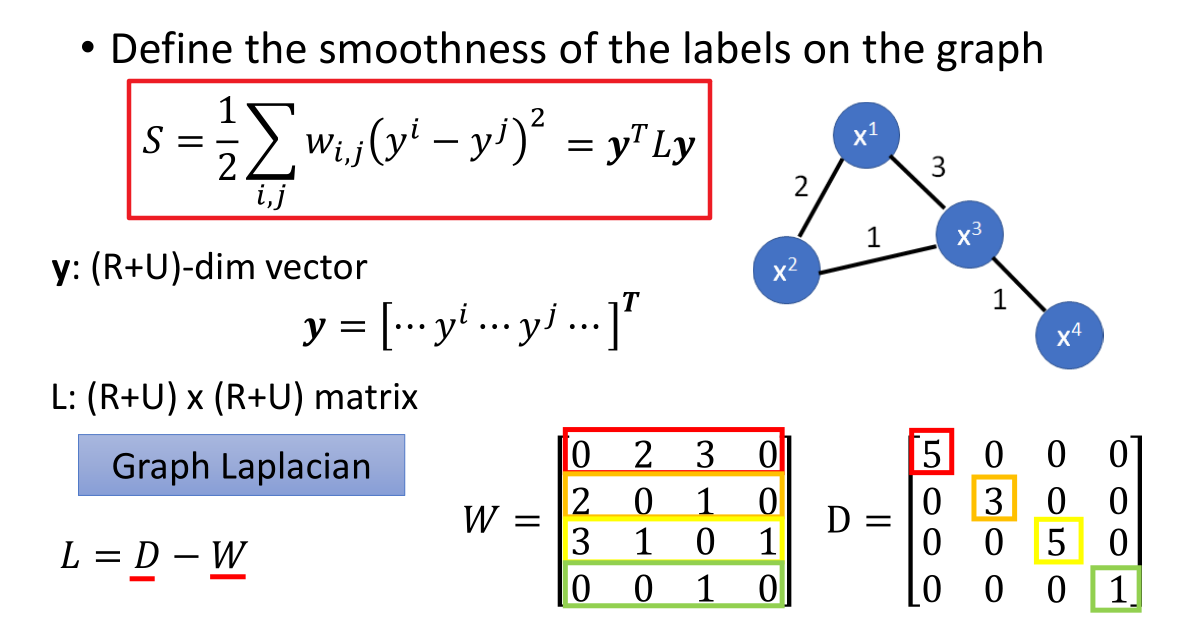$w_{i,j}$ 表示图中两个点之间的权重；矩阵 $W$ 则是由 $w_{i,j}$ 组成的权重矩阵。
矩阵 D 中对角线元素的值为 $W$ 矩阵中每行元素的和。
$y$ 是数据样本的标签值组成的向量（既包含了有标签的数据，也包含了无标签的数据）；向量的维度为 (R+U)。
L 相应的就是一个 (R+U)×(R+U) 的一个矩阵，叫做图拉普拉斯矩阵，定义为 L=D−W。
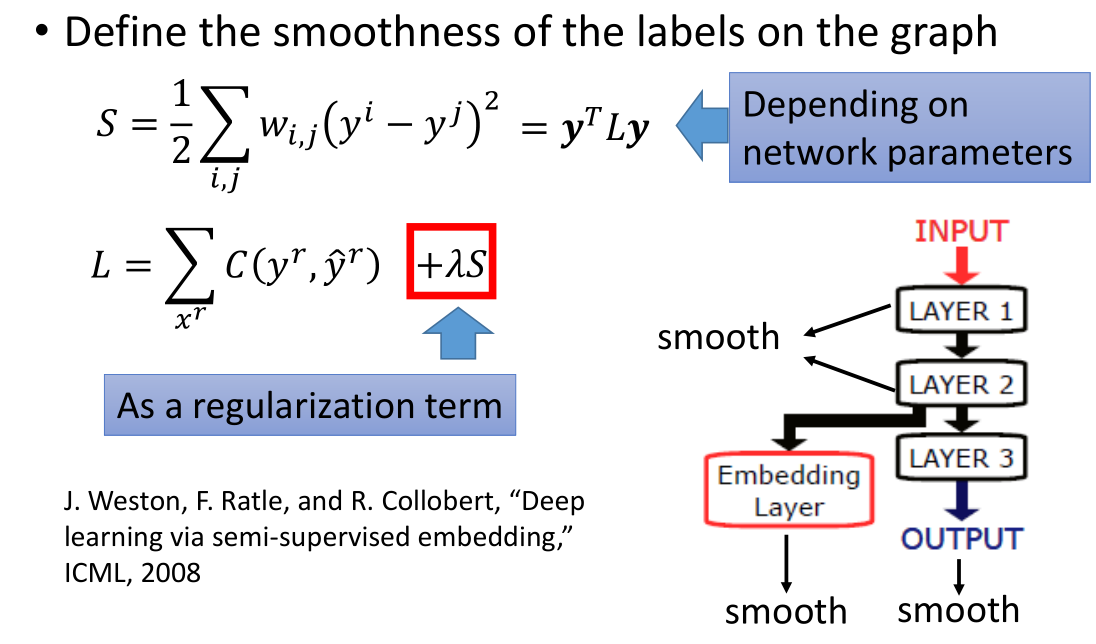
平滑度 S 的值是取决于网络参数的，为了将平滑度的影响加入到网络的训练过程中，
我们将平滑度 S 作为正则项加入到损失函数中，得到 $L=∑_{x^r}C(y^r,\hat{y}^r)+λS$。
我们在不仅需要考虑有标签数据给损失函数带来的影响 $C(y^r,\hat y^r)$，还需要考虑无标签数据产生的影响 $\lambda S$。
当我们的模型是深度网络的时候，我们可以将平滑度放在网络中的任何位置。
5.更好的表达
主要思想是“去芜存菁，化繁为简”。指的是要抓住重点，得到更好的表达。
找到在观察(observation)下的潜在因素（latent factor），这些潜在的因素(通常更简单)是更好的表达(better represevtation)。
上图漫画中，胡子是观察，头才是重点是更好的表达。
关于这方面的内容在非监督学习中将会重点讲解。
7.总结
本小节讲述了半监督学习：
- 生成模型中的半监督学习
- 低密度分离
- 平滑性假设
- 更好的表达