这一节我们主要学习

• 理解题意，运用回归实现PM2.5预测

1 任务描述 (Task Description)

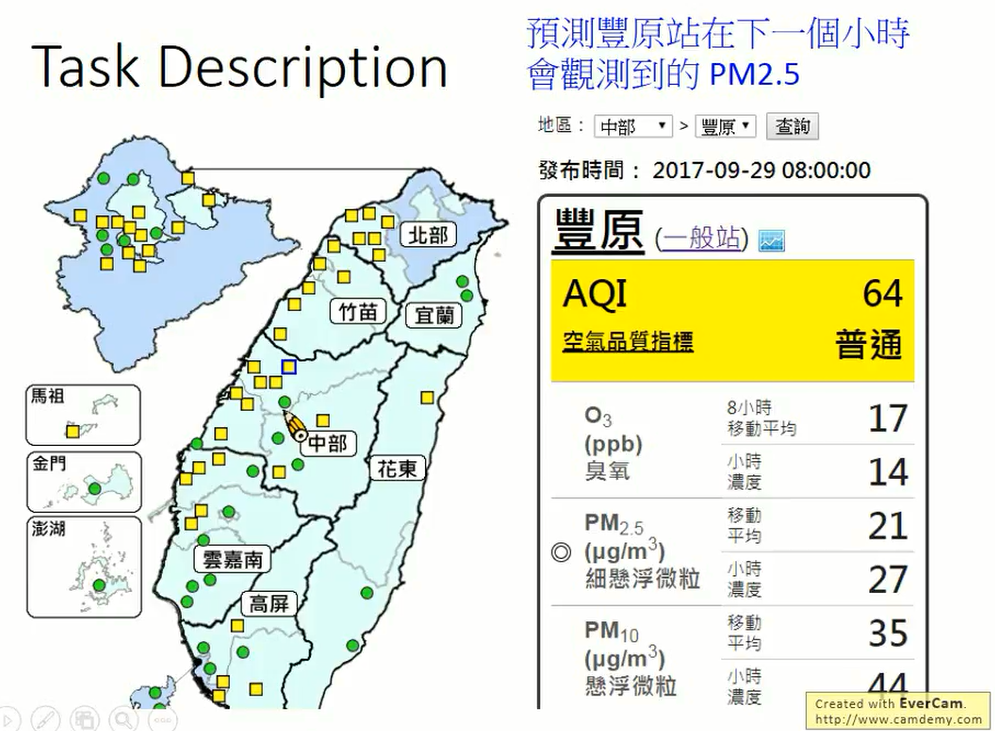
预测丰原站下一个小时会观测到的PM2.5
中国台湾地图上黄点和绿点代表气象观测站的位置
黄色表示空气质量指标比较差
绿色表示空气质量指标比较好

2 介绍数据集

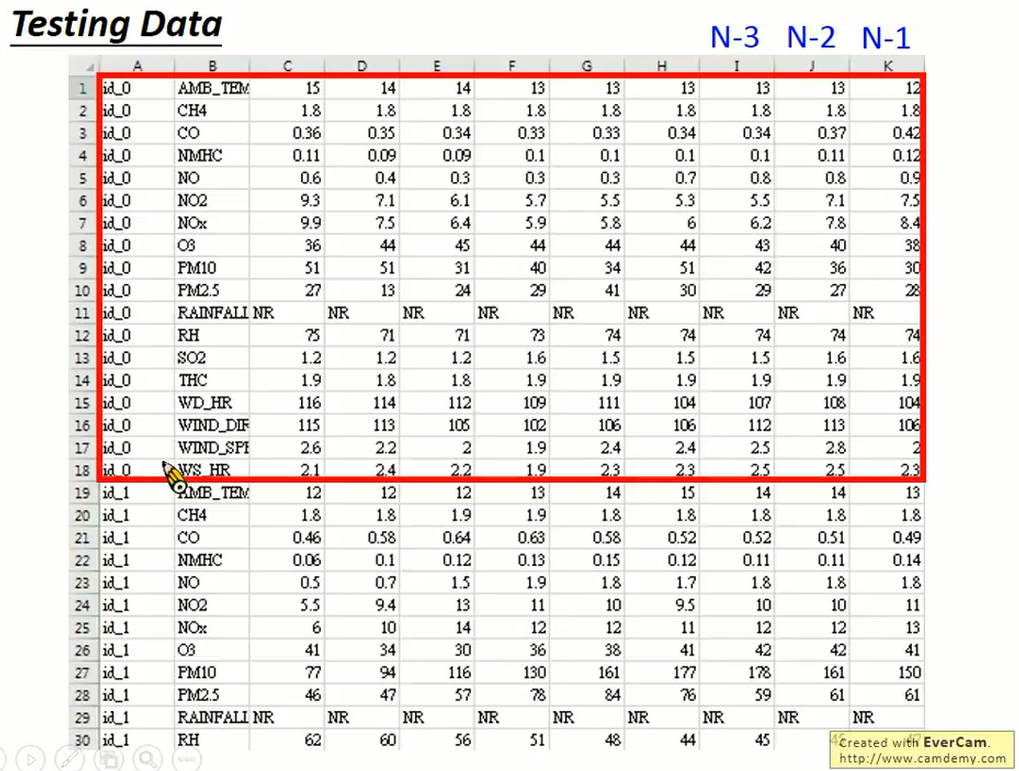
第 A 列是id：每一个id代表一个时间点；
第 B 列是各项指标；
第 K 列表示第 N-1 时的指标值。

3 机器学习第一步：定义你的模型

预测值y：A年B月C日 N时的PM2.5

输入值$x_{K,M}：$A年B月C日 N-K 时的 M 观测值

M = PM2.5，CH4， NO， NO2， O3 …(总共18种)

数据集中某些指标不是数值，比如RAINFALL = NR，该怎么表示呢？

• 假设说PM2.5 仅与过去9个小时的PM2.5 相关，则：
  

$ y = b + w_{1,PM}·x_{1,PM}+ w_{2,PM}·x_{2,PM}+…+ w_{9,PM}·x_{9,PM}$

• 假设说PM2.5 仅与过去5个小时的PM2.5 相关，则：

$ y = b + w_{1,PM}·x_{1,PM}+ w_{2,PM}·x_{2,PM}+…+ w_{5,PM}·x_{5,PM}$

• 假设说PM2.5 与过去5个小时的PM2.5和N0，O3,… 相关，则：

\begin{aligned} y = b & + w_{1,PM}·x_{1,PM}+ w_{2,PM}·x_{2,PM}+…+ w_{5,PM}·x_{5,PM}
& + w_{1,NO}·x_{1,NO}+ w_{2,NO}·x_{2,NO}+…+ w_{5,NO}·x_{5,NO}
& + w_{1,O3}·x_{1,O3}+ w_{2,O3}·x_{2,O3}+…+ w_{5,O3}·x_{5,O3}
&…… \end{aligned}

4 机器学习第二步：根据训练集确定损失函数

训练集来自每个月的前20天；
测试集来自每个月的后10天；
从训练集中拿出一些数据集作为验证集（2：8/3:7)

5 机器学习第三步：找到最好的模型

采用梯度下降法找到最好的模型

线性代数正规方程求解与梯度下降法的解形成对比。