02-01 线性回归案例

线性回归的案例研究

线性回归模型的应用场景
机器学习相关的名词，比如：特征、模型、损失函数、训练集、测试集、误差、线性模型、过拟合等
线性回归模型的原理和实现流程
梯度下降法
过拟合产生的原因以及解决方法
正则化

1. 回归的定义

回归模型：

输入：预测对象的各种已有信息
输出：输出值是一个数字

回归模型可以做很多事情。比如道琼斯指数预测、自动驾驶中的方向盘角度预测，

以及推荐系统中预测客户购买某种商品的可能性等等。

李老师课程中的案例是运用回归模型来预测宝可梦 (pokemons) 进化后的CP值。

预测股票市场
商品推荐

2. 回归模型案例：预测宝可梦进化后的CP值

根据宝可梦已有的攻击力 Combat Power(CP) ，估算出它进化后的攻击力 (CP) 。

这里我们的任务就是找到一个 function ，能够准确预测宝可梦的CP值。

function 的输入就是宝可梦进化前的各种资讯信息，输出就是宝可梦的CP值。

在这里我们使用第一节的机器学习三大步骤流程来处理：

第一步：选择一系列的函数（a set of function），即选择一个模型（model）
第二步：评价函数的优劣（goodness of function）
第三步：选出最好的那个函数（best function）

2.1 第一步：建立机器学习模型

一只宝可梦可由5个参数表示，$x=(x_{cp}, x_s, x_{hp}, x_w, x_h)$ 。

我们的模型先选择线性模型，对以上的输入解释：

$x_{cp}$：宝可梦进化前的CP值；

$x_s$：宝可梦的物种(种类)；

$x_{hp}$：宝可梦的HP值；

$x_w$：宝可梦的重量；

$x_h$：宝可梦的高度，

输出： $y$：一个数值，表示宝可梦进化后的CP值。

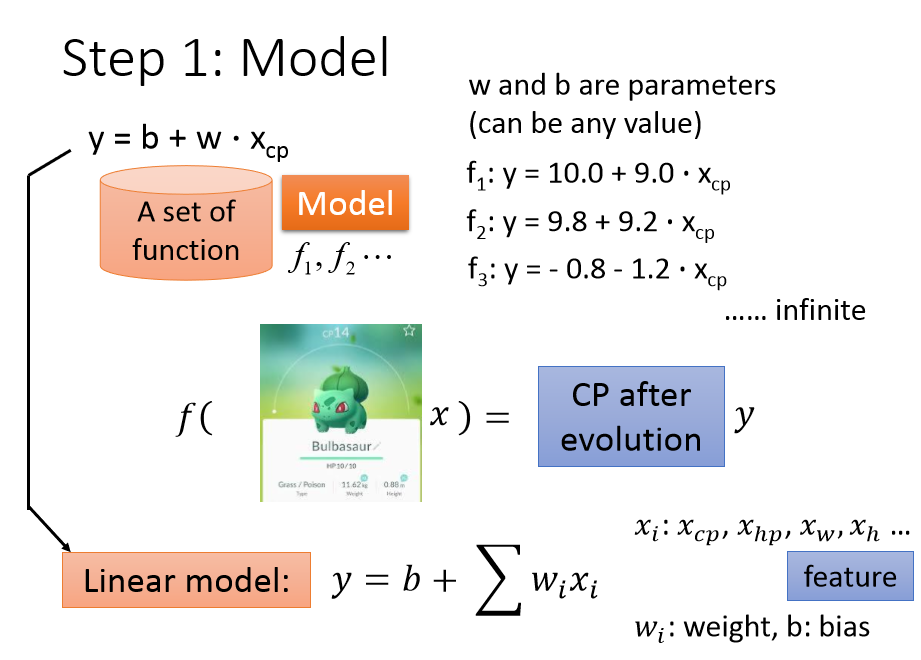
我们假设输出值 y 与输入值 $x_{cp}$ 有这样的关系：

$y=b+w·x_{cp}$ （$w$ 和 $b$ 称作参数，可以是任何值）

对于不同的对 $w$ 和 $b$ ，得到的模型也不尽相同，而我们需要找到最适合的模型。

对 $w$， $b$ 输入不同的值，得到的 function 就是 function set，

function set 包含 $f_1$，$f_2$，$f_3$ 等各种模型。

这里面的模型有合理的，也有不合理的，

比如 $f_3$ 就不合理，因为 $w$，$b$ 若都是负数，而则输出值 y 就是负数，

CP值是负数，显然是不合理的。

有无穷多个函数就组成了线性模型，关系表达式如下：

$y = b+\sum w_ix_i $

其中 $x_i:(x_{cp}, x_s, x_{hp}, x_w, x_h …)$，输入值宝可梦的特征 $x_i$ 被称作特征，

$w_i$ 称作权重，$b$ 称作偏置。

到目前为止，我们已经只做好了一个 model。

2.2 第二步：评价模型

它类似于函数的函数，我们输入一个函数，输出的是 how bad it is，这就需要定义一个损失函数，用来判断我们模型的好坏。

用已经知道的不同的输入值可以训练出来不同的宝可梦的 CP 值。

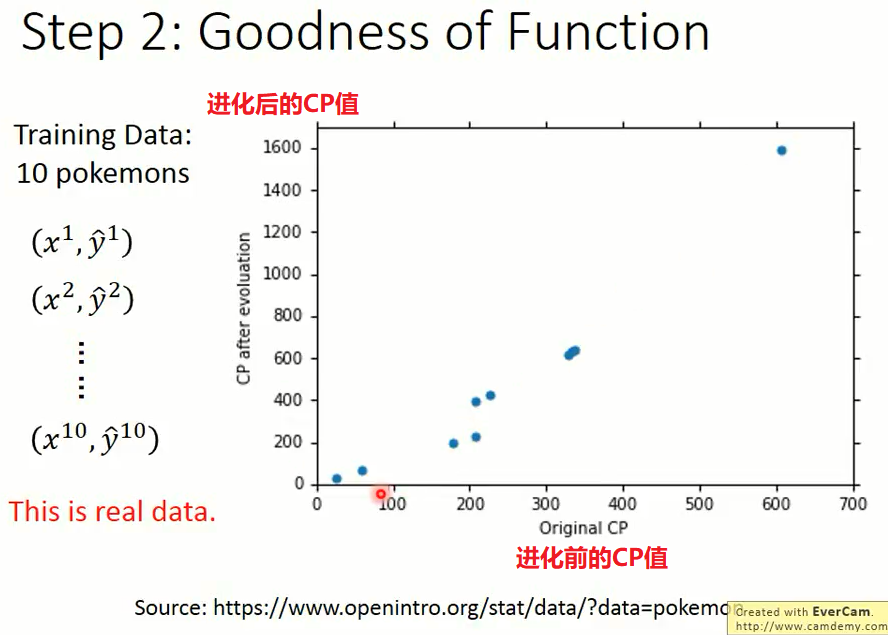
下图是 10 只宝可梦的数据集，其中：

$ x^{1},…,x^{10}$ 表示10只宝可梦进化前的信息值

$ y^{1},…,y^{10}$ 表示10只宝可梦进化后的CP值

模型的平方损失函数：

$L(f) = \sum_{n=1}^{10}[y^n-f(x_{cp}^n )]^2 $

其中： $y^n$ 表示第n个宝可梦CP的的真实值

$f(x_{cp}^n)$ 表示第$n$只宝可梦CP的预测值

考虑到预测值y与参数$w$和$b$的关系,将上式转化如下：

$ L(f) = \sum_{n=1}^{10}[y^n-(b+w·x_{cp}^n)]^2$

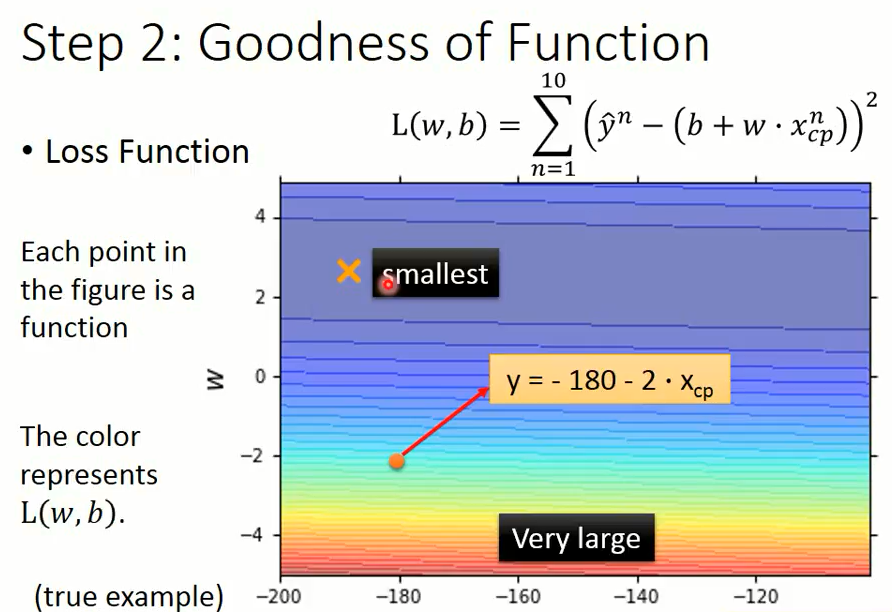
上图为二维平面图，图中每一个点代表一个function，

横轴表示 $b$ 的大小，纵轴表示 $w$ 的大小，颜色的深浅表示 loss 值的大小，

红颜色表示 loss 的值越大，绿灰色表示 loss 的值越小。

比如：$w$ 为负数越小，预测出来的 CP 值与实际的 CP 值差距也就越大，红颜色也就越深。

但是在实际工作中，参数比较多，所以无法使用穷举法来选择模型。

2.3 第三步：如何挑选到最好的模型

每个 function 都有自己的损失值，选择最好的模型即是选择损失函数值最小的 function。

求解最优参数的方法(图片中最后一个式子)可以用线性代数的基本公式来直接计算出最佳的 w 和 b。

当特征非常多时，我们就可以用 **梯度下降法 (Gradient Descent) ** 进行求解。

3. 梯度下降法(Gradient Descent)

3.1 我们首先仅仅考虑一个参数 $w$ 对损失函数（loss function $L(w)$）的影响

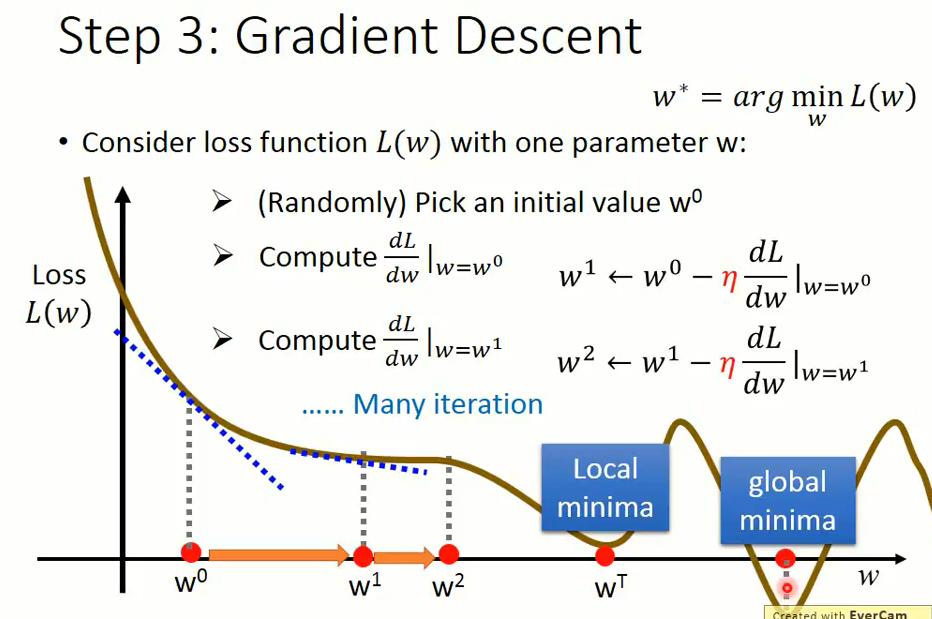
当我们在 $L(w)$ 的二维平面中时，我们必须要找到函数的最低点。

在图像上我们很容易得到全局最优解的位置，但是采用 Gradient Descent，步骤如下：

第一步：随机挑选出来一个 $w_0$，或者称为 $w$ 初始化；
第二步：计算损失函数在 $w_0$ 处的梯度(切线斜率) $\left.\frac{dL}{dw} \right |_{w=w^0}.$；

如果 $\left. \frac{dL}{dw} \right |_{w=w^0}$ 为负数 (Negative)，那么就增加 (Increase) $w$;

如果 $\left. \frac{dL}{dw} \right |_{w=w^0}$ 为正数 (Positive)，那么就减少 (Decrease) $w$

综合上面两种情况后的数学表达式：

$\left. w^1 = w^0 - η\frac{dL}{dw}\right |_{w=w^0}$

$η$：学习率 (learning rate)，手动设置参数。

学习率如果设置比较大，学习比较快，每次步伐跨的比较大；

如果比较小，学习相对就慢一点，每次跨的步伐就小一点。
第三步：迭代第二步。

根据第二步的规则依次迭代 $w^2,w^3,…,w^n$ 直至找到最小 loss 的 $w^T$ 值，此时损失函数的切线斜率等于零。

如果 $w^0$ 从左边开始初始化，往右走，一般走到局部最小值处 (local minima)；

如果 $w^0$ 从右边开始往左边走，就可以走到全局最小值处 (global minima)；

所以不同的地方起始，就会得到不同的结果，这是一个看人品的方法。

3.2 考虑 w、b 两个参数对损失函数的影响？

其实流程与一个参数都是一样的，区别具体如下：

每次初始化参数 $w^0$、$b^0$
然后每次计算 w 和 b 的梯度，第一次的计算结果为：

$\left. \frac{∂L}{∂w}\right |_{w=w^0，b=b^0}$,

$\left. \frac{∂L}{∂b}\right |_{w=w^0，b=b^0}$；
然后更新 (updata) w、b 的表达式如下：

$\left. w^1= w^0 - η\frac{∂L}{∂w}\right |_{w=w^0，b=b^0}$

$\left. b^1= b^0 - η\frac{∂L}{∂b}\right |_{w=w^0，b=b^0}$
依次反复迭代，直至找到 loss function 对 w 和 b 偏微分最小的值。

4. 结果分析

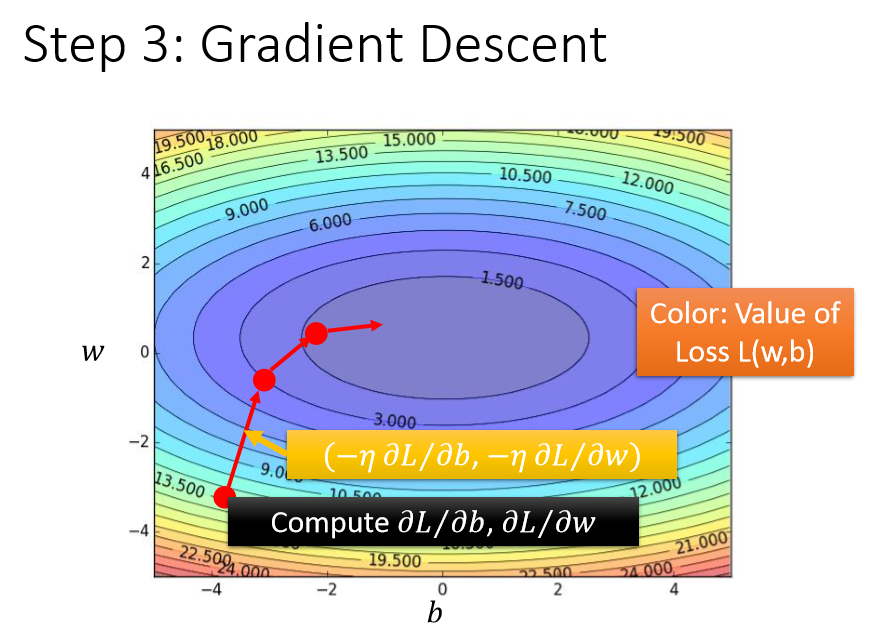
图中横坐标表示偏置 $b$，纵坐标表示权重 $w$，图中颜色的深浅表示 loss 值的大小。

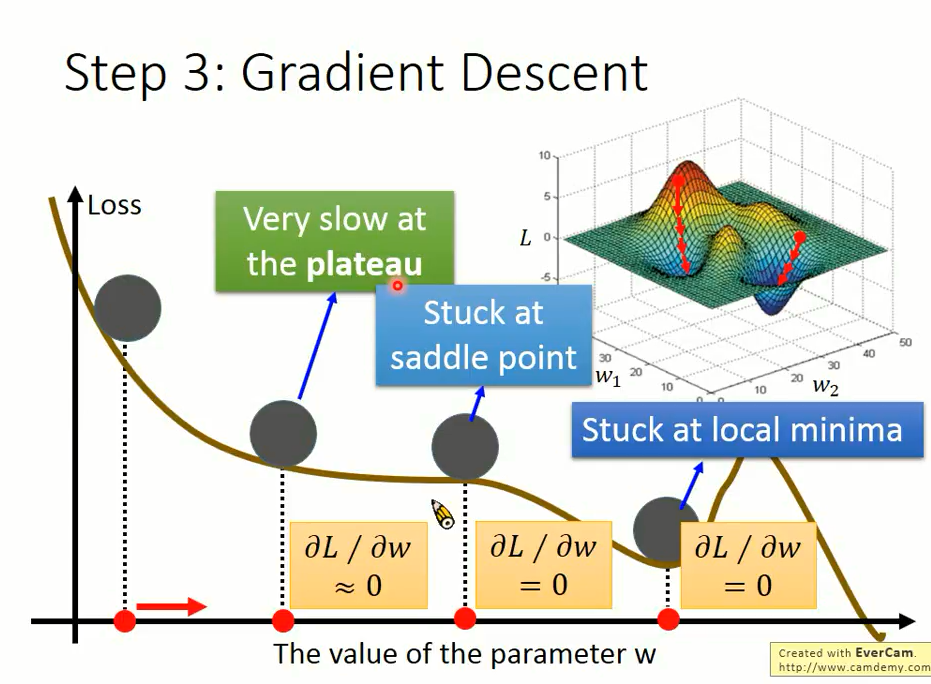
微分是0但却不是极值的点，称为 saddle point，或者函数比较平滑的点，怎么办？

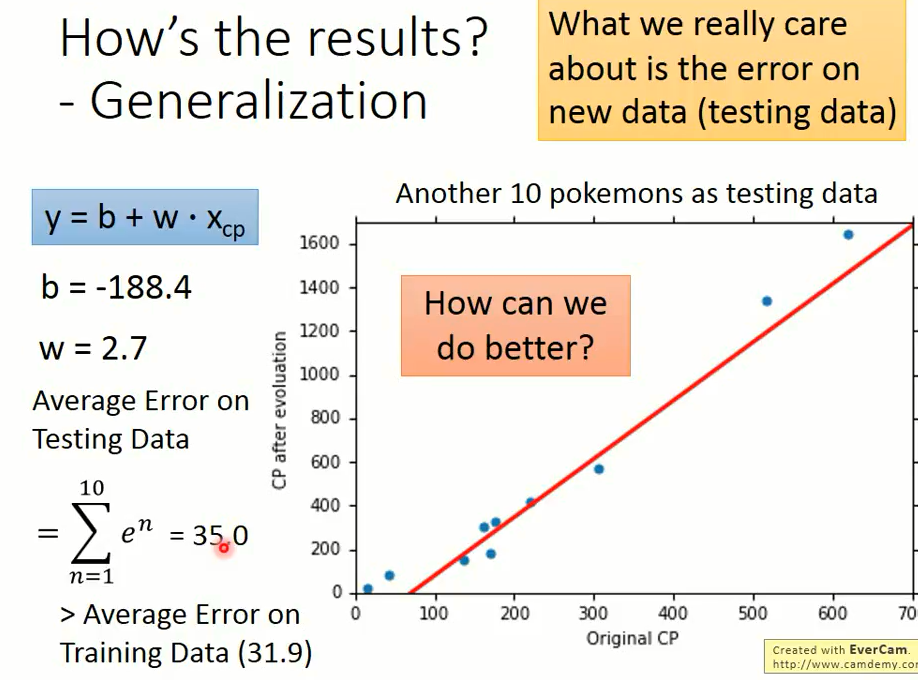
在使用穷举法的时候就已经知道，当 w = 2.7，b = -188.4 的时候就可以获取最好的 function。

然后我们计算平均误差值大小是 31.9。

然后我们采用另外的 10 只宝可梦 CP 值进行预测，平均误差大小是 35.0，跟训练集结果的误差相近。

5. 如何得到更好的模型

刚刚我们选用一次方程作为我们的模型，那么二次方程、三次方程、四次方程会不会更好一点呢？

于是我们采用同样的方法，放到多次方程中，试验结果如下：

那么此时该模型还是还是线性模型吗？以上四个模型依然是线性模型 (linear model)，在这里是将 $(x_{cp})^n$ 看作宝可梦的一个特征处理的。

二次方程
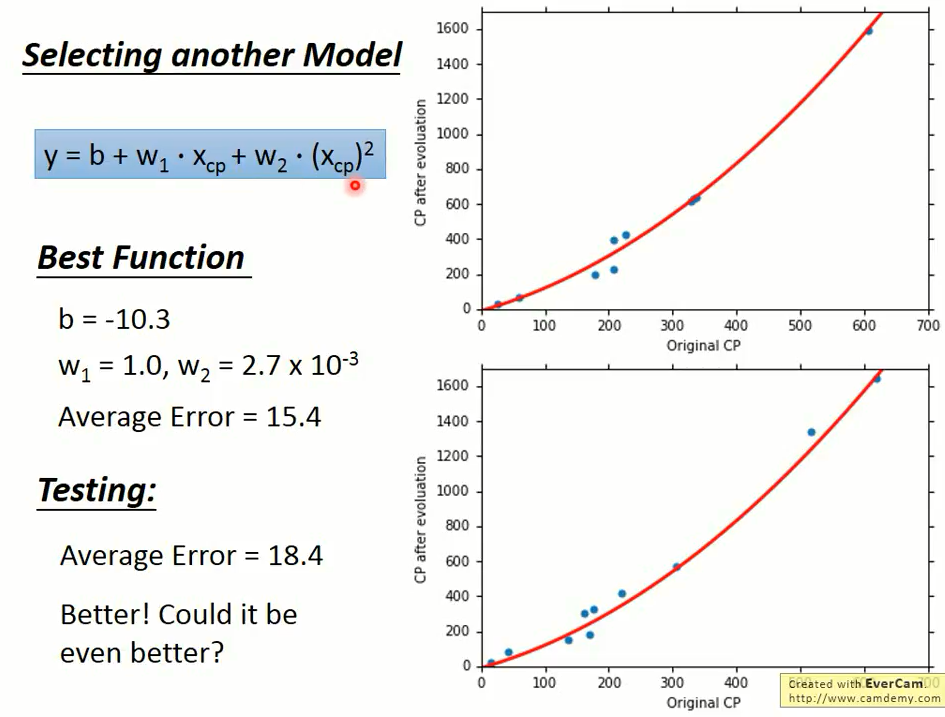
三次方程
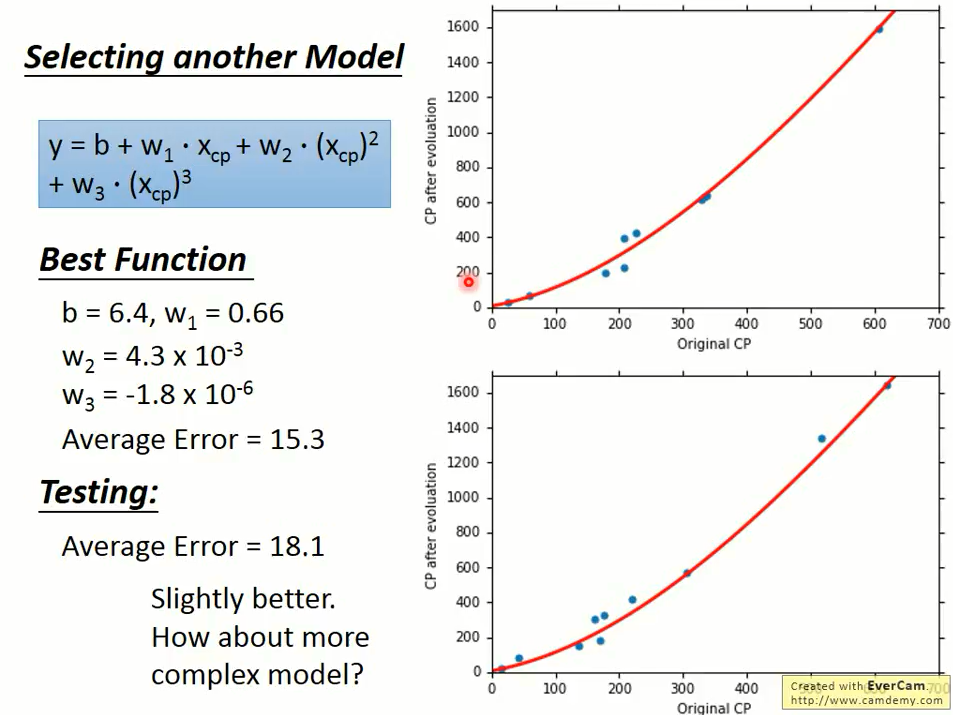
四次方程
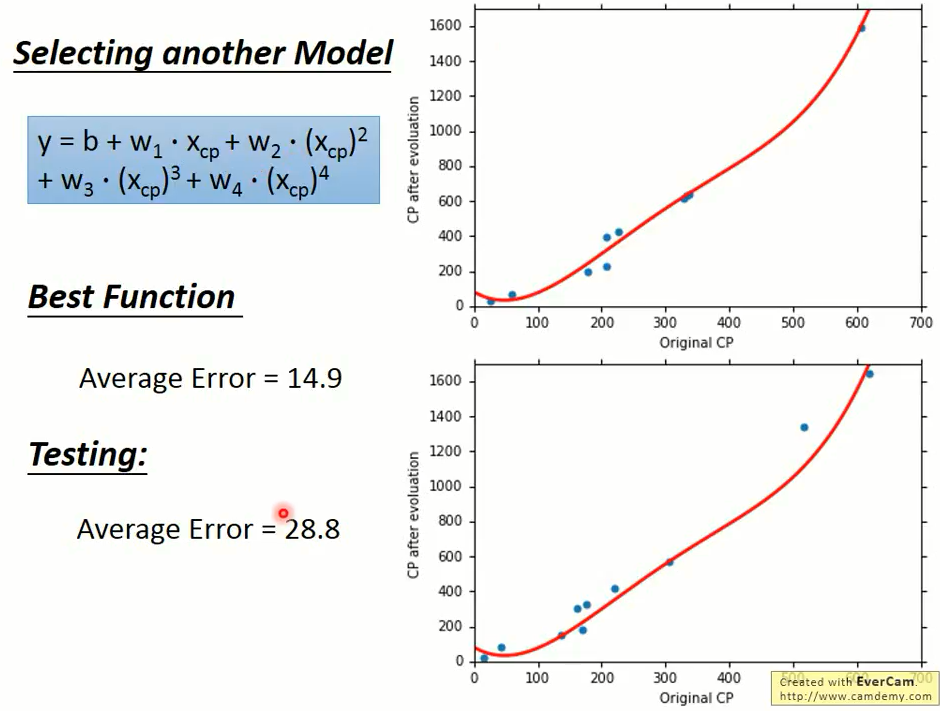
五次方程

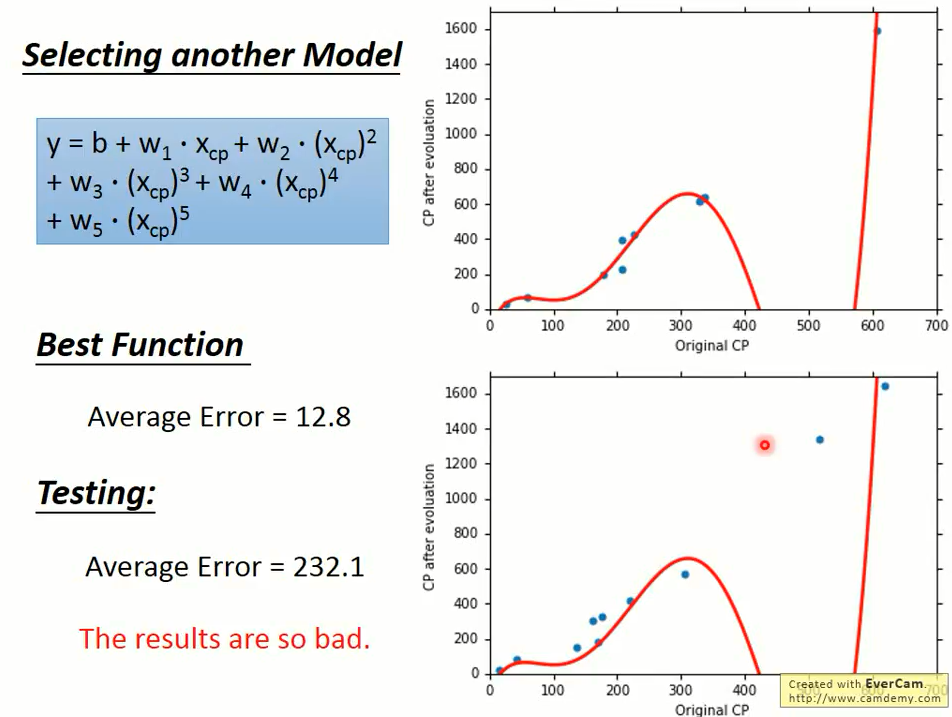
这5个模型都是模型越复杂得到的误差越小，这件事情是很直觉的。

在这里黄色的是第三个模型，绿色的是第 4 个模型，发现 3 个函数只是 4 次函数的一个子集和。

我们将 $w_4$ 设置为零，则就成为 3 次的函数，所以 3 次是 4 次的一个子集和，5 次又是 4 次的一个子集和。

所以根据训练集找到一个最好的函数，在 5 次的集合里面找到最好的函数，不可能比在 4 次集合里面找到最好的函数还要更差。

当我们的模型越复杂，当在训练集上面我们的误差是越来越低的。

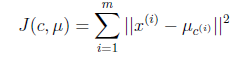
上图中的蓝色线型是训练集上的误差，橙色线型是测试集上的误差，横坐标表示第几个模型。

我们发现在测试集上的误差是三次的时候是最好的，

当模型越来越复杂的时候，误差就会突然爆炸，所以一个复杂的模型在训练集上给我比较好的 performance。

但并不总是在测试集上给我们比较好的 performance，这件事情叫做过拟合 (overfitting)。

从上图我们看到，当第四次拟合的时候，过拟合发生了，测试集上的误差变得很大。

因此，模型不是越复杂越好，而是要选择一个最合适的，综合比较三次方程表现的最好。

虽然它在训练集上不是最好的，但是它在测试集上是最好的。

6. 过拟合解决方式

过拟合的解决方式：

1.收集更多的数据;
2.正则化

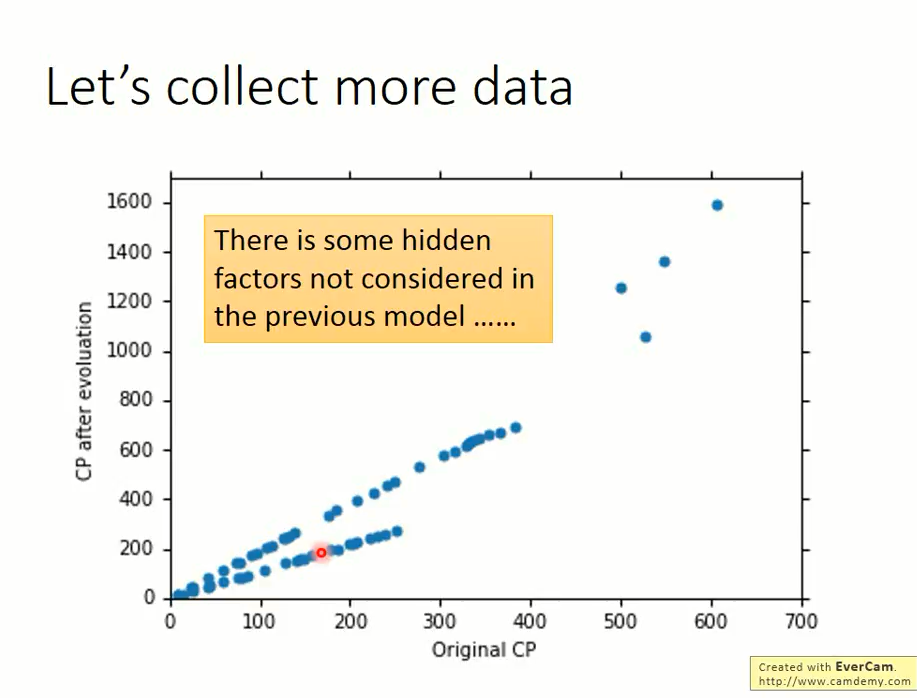
我们收集了 60 只左右的宝可梦进化前后的 CP 值，显然刚刚有我们没有考虑到的一个因素决定了宝可梦的 CP 值，

不然你会发现进化前同样的 CP 值，进化后 CP 值的大小却相差那么多。

那么隐藏的决定性因素又是是什么呢？

通过研究发现，宝可梦进化前后的CP值跟宝可梦的种类有关。

上图中蓝色的是 Pidgey，红色的是 Eevee，黄色的是 Weedle，绿色的是 Caterpie。

因此，现在我们需要设计一个考虑宝可梦种类的模型。

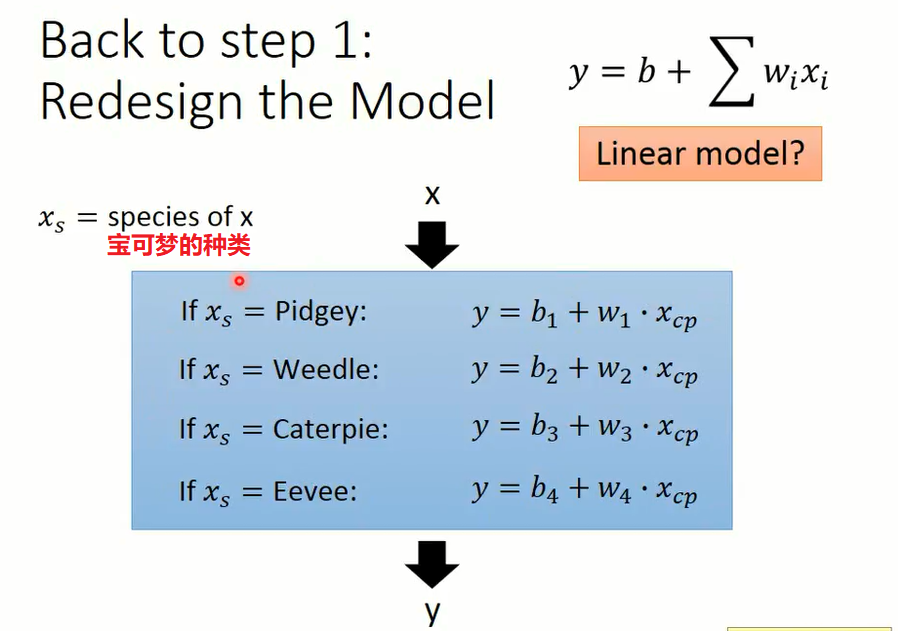
该模型目前还是不是线性模型呢？具体情况可以看下图以及相关的公式：

考虑宝可梦种类后宝可梦CP值预测模型的表达式：

$\begin{aligned} y=b_1·\delta{(x_s = Pidgey)} + w_1·\delta(x_s = Pidgey)x_{cp}+ b_2·\delta(x_s = Weedle) + w_2·\delta(x_s = Weedle)x_{cp}+ b_3·\delta(x_s = Caterpie) + w_3·\delta(x_s = Caterpie)x_{cp} + b_4·\delta(x_s = Eevee) + w_4·\delta(x_s = Eevee)x_{cp} \end{aligned}$

其中：

$δ(x_s = Pidgey)=\begin{cases}1 \text{if x_s=Pidgey} \text{otherwise}\end{cases}$

同理 $δ(x_s = Weedle)$、 $δ(x_s = Caterpie)$、$δ(x_s = Eevee)$。

因此，当 $x_s = Pidgey$ 时，上述表达式就可以化简为：

$\begin{aligned} y = b_1·1 + w_1·1·x_{cp}+ b_2·0 + w_2·0·x_{cp}+b_3·0+ w_3·0·x_{cp} + b_4·0 + w_4·0·x_{cp} =b_1 + w_1·x_{cp}\end{aligned}$

同理，当 $x_s = $Weedle 时，$y=b_2 + w_2·x_{cp}$；

当 $x_s = $Caterpie 时，$y=b_3 + w_3·x_{cp}$；

当 $x_s = $Eevee 时， $y =b_4 + w_4·x_{cp} $，

因此，此时该模型还是线性模型。

此时我们绘制出来四条曲线，其中有两条重合在一起。

此时我们发现在训练集上误差 3.8，在测试集上误差 14.3；

我们在上一个模型中，最好的 function 中，在训练集上的误差 15.3，在测试集上的误差 18.1。

是否还有其他隐藏的因素呢？

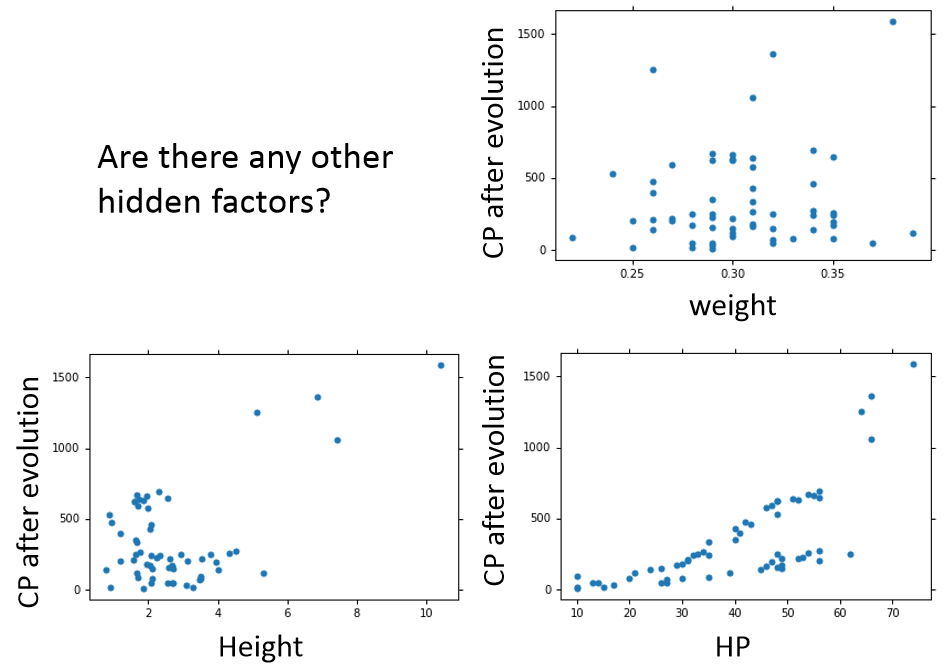
比如重量，高度，HP 是否有用呢？不知道哪些 features 有用，那么我们就直接用全部的 features。

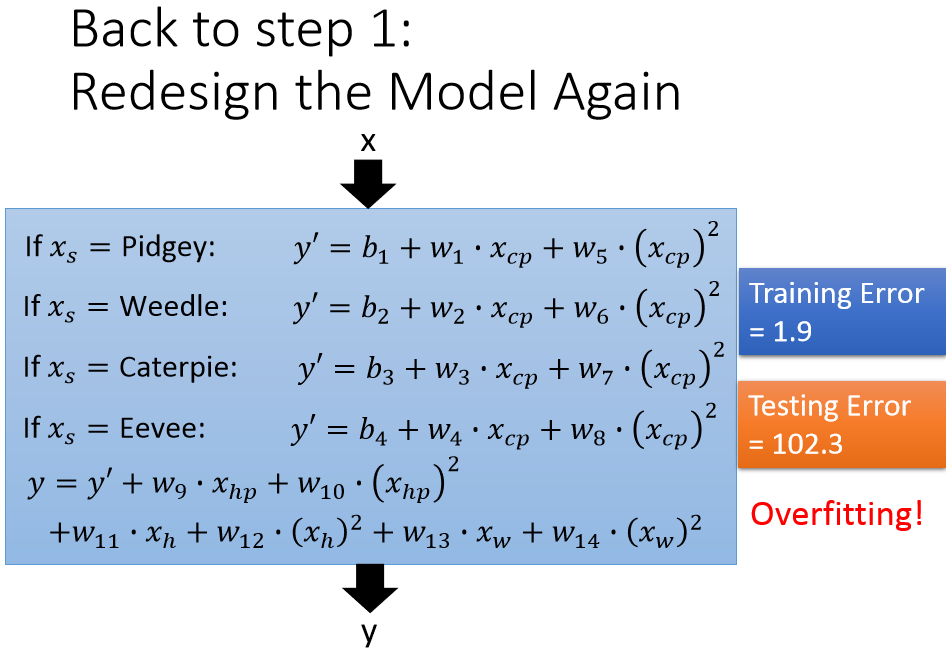
以上模型一共 18 个参数，也不算多。然后我们计算训练集误差为 1.9，测试集误差为 102.3，发现过拟合了！下面介绍另外一种方法防止过拟合。

正则化

正则项：$\lambda\sum{(w_{i})^2}$

正则项越小，意味着 $w_i$ 越小，同时也说明损失函数比较平滑。

平滑的理解是输入的变化很大而输出的变化很小，则 function 是比较平滑的。

为什么我们要选择既让损失函数小的 function，同时又要一个 smoother 的 function？

因为一般情况，smoother function 更倾向于正确的那个模型；
为什么正则化没有考虑 bias？

一方面，y = bias是一条水平线，对function是否平滑没有影响；

正则化结果：

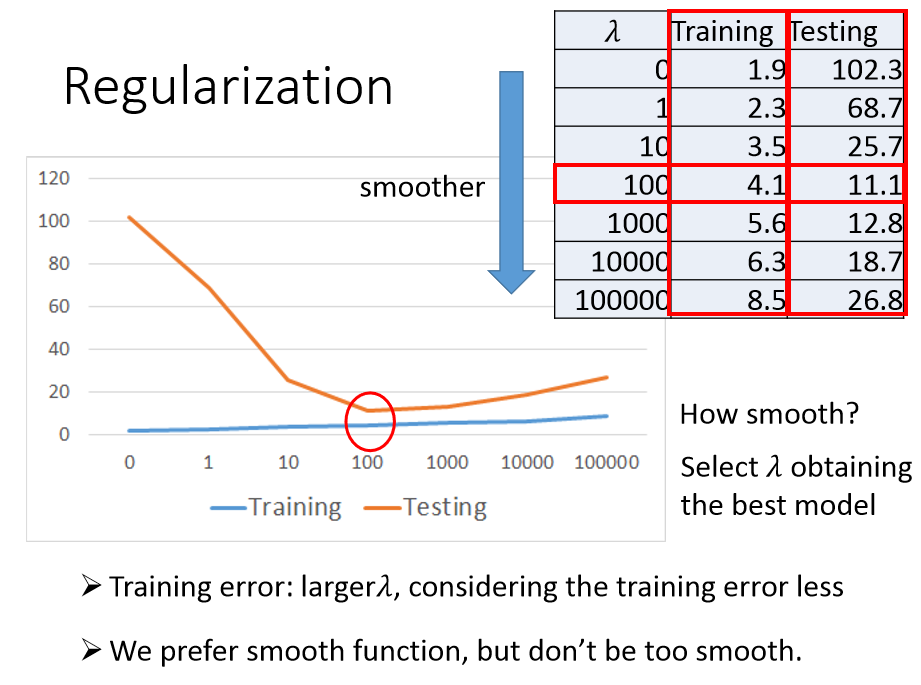
$\lambda$ 是手动调整的。

在宝可梦CP值预测的模型上，$\lambda$ 越大，在训练集上的误差是越来越大的，测试集上的误差是先降低后增大。

因此我们更偏向于平滑的 function，但是要考虑训练集误差，故也不能太平滑。

因此选择参数 $\lambda$ 值也很重要，具体方法请参考后续课程。

7.总结：

宝可梦进化后的 CP 值显然跟宝可梦的种类和进化前的CP值有关系
- 可能还有其他的隐藏因素，目前还未研究出来
梯度下降法
- 更多的理论和推到细节放在后续课程中
我们最终得到在测试集上误差为 11.1 的机器学习模型
- 我们的模型对新数据如何？如果新数据放在我们的模型中，得到的误差会大于 11.1 还是小于 11.1?
下节课：误差的来源？